1、某单位职工24人中，有女性11人，已婚的有16人。在婚的16人中有女性6人。问这个单位的未婚男性有多少人?_____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释:答案：B【解析】男性人数为：24-11=13，已婚男性为l6-6=10（人），因此，未婚男性为13-10=3（人），故选B。

2、某玩具店同时卖出一个拼装玩具和一架遥控飞机，拼装玩具66元，遥控飞机120元，拼装玩具赚了10%，而遥控飞机亏本20%，则这个商店卖出这两个玩具赚钱或是亏本多少?_____
A: 赚了12元B: 赚了24元C: 亏了14元D: 亏了24元
参考答案: D 本题解释:【答案】D。解析：二者成本分别为66÷（1+10%）=60元、120÷（1-20%）=150元，成本合计为60+150=210元，亏了210-66-120=24元。

3、173×173×173-162×162×162=_____。
A: 926183B: 936185C: 926187D: 926189
参考答案: D 本题解释:答案：D【解析】利用简单的猜测法。173的尾数是3，3的立方为27;162的尾数是2，2立方为8。两者相减尾数为9，所以判断173和162的立方之差的尾数为9。所以答案为D项。

4、A、B、C、D四支球队开展篮球比赛，每两个队之间都要比赛1场，已知A队已比赛了3场，B队已比赛了2场，C队已比赛了1场，D队已比赛了几场？（）
A: 3B: 2C: 1
参考答案: B 本题解释:每个球队要比赛3场，则A队和B队、C队、D队各比赛1场，C队和A队比赛1场，B队和A队、D队各比赛1场，故D队比赛了2场。所以选B。

5、某储户于1999年1月1日存入银行60 000元，年利率为2.00％，存款到期日即2000年1月1日将存款全部取出，国家规定凡1999年11月1日后孳生的利息收入应缴纳利息税，税率为20%，则该储户实际提取本金合计为_____。
A: 61 200元 B: 61 160元C: 61 000元 D: 60 040元
参考答案: B

6、甲、乙两地相距100千米，张先骑摩托车从甲出发，1小时后李驾驶汽车从甲出发，两人同时到达乙地。摩托车开始速度是50千米/小时，中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟，那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 1(1/2)C: 1/3D: 2
参考答案: C 本题解释:C解析：汽车行驶100千米需100÷80=1（1/4）（小时），所以摩托车行驶了1（1/4）+1+,1/6=2（5/12）（小时）。如果摩托车一直以40千米/小时的速度行驶，2（5/12）小时可行驶96（2/3）千米，与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷（50-40）=1/3（小时）。故本题选C。

7、小张、小王二人同时从甲地出发，驾车匀速在甲乙两地之间往返行驶。小张的车速比小王快，两人出发后第一次和第二次相遇都在同一地点，那么小张的车速是小王的_____倍。
A: 1.5B: 2C: 2.5D: 3
参考答案: B 本题解释:【解析】B。行程问题。采用比例法。由题意，两人从同地出发，则第一次相遇时两人的路程和为2个全程，设其中小张走了x，小王走了y；第二次相遇 时两人走了4个全长，小张走了2y，小王走了x-y；由比例法x÷y=2y÷（x-y），解得x=2y，故两人速度比为2：1。

8、建华中学共有1600名学生，其中喜欢乒乓球的有1180人，喜欢羽毛球的有1360人，喜欢篮球的有1250人，喜欢足球的有1040人，问以上四项球类运动都喜欢的至少有几人？_____
A: 20人B: 30人C: 40人D: 50人
参考答案: B 本题解释:【答案】B。解析：采取逆向思维法。不喜欢乒乓的1600－1180＝420，不喜欢羽毛球的1600－1360＝240，不喜欢篮球的1600－1250＝350，不喜欢足球的1600－1040＝560，要使四项运动都喜欢的人数最少，那么不喜欢的人数就要最多那么都尽量不相交，从而达到最多：420＋240＋350＋560＝1570人，所以喜欢的最少的为1600－1570＝30人，故正确答案为B。

9、为帮助果农解决销路，某企业年底买了一批水果，平均发给每部门若干筐之后还多了12筐，如果再买进8筐则每个部门可分得10筐，则这批水果共有_____筐。
A: 192B: 198C: 200D: 212
参考答案: A 本题解释:【答案】A。解析：总数加8应能被10整除，如果为A，则部门数为20；如果为D，部门数为22，则212÷22=9……14不符合题意。故选择A。

10、小赵、小王、小李和小陈四人，其中每三个人的岁数之和分别为65、68、62、75其中年龄最小的是多少岁?_____
A: 15 B: 16 C: 17 D: 18
参考答案: A 本题解释:A【解析】设四人年龄从大到小依次为A、B、C、D则有A+B+C+=75，B+C+D=62，A+B+D=68，A+C+D=65将四个“年龄和”相加可得3（A+B+C+D）=65+68+62+75=270则A+B+C+D=90故D的年龄为90-75=15岁，故应选择A选项。

11、三河村与县城相距18千米。王秘书从三河村委去县城办事。他走1.5千米时，通讯员小张发现王秘书忘了带东西，于是立即追赶。小张追上小王秘书后，马上返回村委，这时王秘书忘了带东西，于是立即追赶。小张追上王秘书后，马上返回村委，这时王秘书也刚到县城。已知小张比王秘书每小时多走1千米，王秘书和小张的速度各是多少?_____
A: 4千米/时B: 5千米/时C: 5.5千米/时D: 6千米/时
参考答案: C 本题解释:【解析】C。王秘书的速度为（18-1.5）÷（1.5÷1×2）=5.5千米/时。

12、把一个边长为4厘米的正方形铁丝框拉成两个同样大小的圆形铁丝框，则每个圆铁丝框的面积为_____。
A: AB: BC: CD: D
参考答案: D 本题解释:D【解析】设铁丝拉成的圆的半径为r，则4×4=2×2πr，r=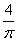，圆形面积S=πr2=。

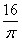13、从0，1，2，7，9五个数字中任选四个不重复的数字，组成的最大四位数和最小四位数的差是_____。
A: 8442B: 8694　C: 8740D: 9694
参考答案: B 本题解释:答案：B。由题意可得：最大的四位数为9721，最小的四位数为1027，故两者的差是9721-1027=8694。

14、如下图所示，X、Y、Z分别是面积为64、180、160的三张不同形状的纸片。它们部分重叠放在一起盖在桌面上，总共盖住的面积为290。且X与Y、Y与Z、Z与X重叠部分面积分别为24、70、36。问阴影部分的面积是多少？（）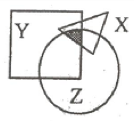
A: 15B: 16C: 14D: 18
参考答案: B 本题解释:【答案】B。解析：直接应用三集合容斥原理公式，可知：290＝64＋180＋160－24－70－36＋X，则290＝（64－24）＋（180＋160）－70－36＋X，即290＝40＋（180＋160）－70－36＋X，X＝16，故正确答案为B。

15、一个两位数等于其个位数字的平方与十位数字之和，这个两位数是_____。
A: 10B: 76C: 89D: 45
参考答案: C 本题解释:C

16、某商场开展购物优惠活动：一次购买300元及以下的商品九折优惠;一次购买超过300元的商品，其中300元九折优惠，超过300元的部分八折优惠。小王购物第一次付款144元，第二次又付款310元。如果他―次购买并付款，可以节省多少元?_____
A: 16B: 22.4C: 30.6D: 48
参考答案: A 本题解释:A【解析】统筹优化问题。由题意，第一次付款144元可得商品原价为160元;第二次付款为310元，可得原价为350元。故总价510元，按照优惠，需付款300×0.9+210×0.8=438元，节省了454-438=16元。

17、筑路队原计划每天筑路720米，实际每天比原计划多筑路80米，这样在规定完成全路修筑任务的前3天，就只剩下1160米未筑，这条路全长多少千米?_____
A: 8.10B: 10.12C: 11.16D: 13.50
参考答案: C 本题解释:【解析】：现在每天筑路：720+80=800（米）规定时间内，多筑的路是：（720+80）×3-1160=2400-1160=1240（米）求出规定的时间是1240÷80=15.5（天），这条路的全长是,720×15.5=11160（米）。故本题选C。

18、一列长90米的火车以每秒30米的速度匀速通过一座长1200米的桥，所需时间为_____。
A: 37秒B: 40秒C: 43秒D: 46秒
参考答案: C 本题解释:C【精析】火车过桥实际走过的距离等于火车的长度加上桥的长度，因此所需时间=(1200+90)÷30=43(秒)。

19、一个车队有三辆汽车， 担负着五家工厂的运输任务，这五家工厂分别需要 7、9、4、10、6 名装卸工，共计 36 名;如果安排一部分装卸工跟车装卸，则不需要那么多装卸工，而只需要在装卸任务较多的工厂再安排一些装卸工就能完成装卸任务。那么在这种情况下，总共至少需要_____名装卸工才能保证各厂的装卸需求?_____
A: 26　　B: 27　　C: 28　　D: 29
参考答案: A 本题解释:【答案】A[解析]要求最少，那么三辆车分别装五家工厂里面最大的三个需求量，则可以满足条件，分别装10、9、7， 所以是10+9+7=26，选A。

20、一车行共有65辆小汽车，其中45辆有空调，30辆有高级音响，12辆兼而有之。既没有空调也没有高级音响的汽车有几辆?_____
A: 2B: 8C: 10D: 15
参考答案: A 本题解释: A 【解析】做这样的题最好用画图法。

21、如图所示，A的面积为36平方米，B的面积为24平方米，A、B之间的落差为5米，现在要将A地的土移到B地，使A、B同样高，B地应升高_____米。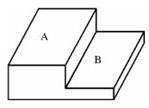
A: 2B: 2.4C: 2.5D: 3
参考答案: D 本题解释:D【解析】图所示，将B面视为水平面，A面所在六面体的体积为36×5=180（立方米），将这180立方米的土平均分布在（A+B）的面上，所得到的高就是B面上升的高度，即180÷（36+24）=3（米），故本题答案为D。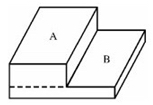

22、5个男生和3个女生排成一排，3个女生必须排在一起，有多少种不同排法？_____
A: 240B: 320C: 450D: 480
参考答案: B 本题解释: 答案【B】采用捆绑法，把3个女生视为一个元素，与5个男生进行排列，共有 A（6，6）=6x5x4x3x2种，然后3个女生内部再进行排列，有A（3，3）=6种，两次是分步完成的，应采用乘法，所以排法共有：A（6，6） ×A（3，3） =320（种）。

23、小雪买了7瓶酸奶，共付款17.5元，喝完全部酸奶退瓶时，知道每个空瓶的价钱比瓶中酸奶的价钱少1.5元，那么小雪应收到退款多少元?_____
A: 5元B: 4.5元C: 3元D: 3.5元
参考答案: D 本题解释:D【解析】设每瓶瓶中酸奶x元，则每个瓶子的押金为（x-1.5）元。则得：7×[x+（x-1.5）]=17.5，解得x=2（元）。所以每个瓶子的押金为2-1.5=0.5元，应退款：7×0.5=3.5元。

24、某乐队举办一场演唱会的收入是7000元，乐队的主唱分得其中的25%，另外5名成员平分余下的收入，那么他们每人分得多少元？_____
A: 1750B: l400C: 1120D: 1050
参考答案: D 本题解释:【解析】D。另外5名成员平分余下的收入，每人拿15%，即1050元。

25、423×187-423×24-423×63的值是_____。
A: 41877B: 42300C: 42323D: 42703
参考答案: B 本题解释: B 【解析】原式可化为423×（187-24-63）。

26、超市经理为某商品准备了两种促销方案，第一种是原价打7折；第二种是买二件赠一件同样商品。经计算，两种方案每件商品利润相差0.1元，若按照第一种促销方案，则100元可买该商品件数最大值是_____
A: 33B: 47C: 49D: 50
参考答案: B 本题解释:【答案】B。解析：设该商品原价为x，则第一种方案下，三件促销价格为2.1x，第二种方案下，三件促销价格2x，两种方案差价为0.1x。根据题意，两种方案每件商品的利润差为0.1元，则三件商品差价0.3元，即0.1x=0.3，解得x=3元，那么按照第一种促销方案，商品售价2.1元，100元最多可以购买该商品47件，选择B项。

27、田忌与齐威王赛马并最终获胜被传为佳话，假设齐威王以上等马、中等马和下等马的固定程序排阵，那么田忌随机将自己的三匹马排阵时，能够获得两场胜利的概率是_____。
A: 2/3B: 1/3C: 1/6D: 1/9
参考答案: C 本题解释:【答案】C。解析：故正确答案为C。

28、银行存款年利率为2.5%，应纳利息税20%，原存1万元1年期，实际利息不再是250元，为保持这一利息收入，应将同期存款增加到_____元。
A: 15000B: 20000C: 12500D: 30000
参考答案: C 本题解释:C。【解析】令存款为x，为保持利息不变，250=x×2.5%×（1-20%）=>x=12500。

29、一个小数去掉小数部分后得到一个整数，这个整数加上原来的小数与4的乘积，得27.6。原来这个小数是_____。
A: 2.60B: 5.65C: 7.60D: 12.65
参考答案: B 本题解释:将原来的小数分成整数部分、小数部分和整个小数。此题可理解为：原小数的4倍与它的整数部分之和为27.6，这样27.6等于5个整数部分与4个小数部分之和。因为4个小数部分之和小于4，可知原小数的整数部分应满足：5倍整数<27<5倍整数+4，所以此整数为5。所以此小数为：5+（27.6-5×5）÷4=5.65，因此，本题正确答案为B。

30、二十几个小朋友围成一圈，按顺时针方向一圈一圈地连续报数。如果报2和200的是同一个人，那么共有_____个小朋友。
A: 22B: 24C: 27D: 28
参考答案: A 本题解释:A【解析】小朋友的人数应是(200-2)=198的约数，而198=2×3×3×11。约数中只有2×11=22符合题意。

31、如果甲比乙多20%，乙比丙多20%，则甲比丙多百分之多少?_____
A: 44B: 40C: 36D: 20
参考答案: A 本题解释: 【解析】A。甲=丙×(1+20%)×(1+20%)=144%丙，则甲比丙多44%。

32、某月的最后一个星期五是这个月的25号，这个月的第一天是星期几?_____
A: 星期二B: 星期三C: 星期四D: 星期六
参考答案: A 本题解释:A 【解析】因为25=3×7+4，所以这个月的4号也是星期五，故这个月的第一天是星期二。

33、某月刊每期定价5元。某单位一部分人订半年，另一部分人订全年，共需订费480元；如果订半年的改订全年，订全年的改订半年，那么共需420元。共有多少人订了这份期刊？
A: 25B: 20C: 15D: 10
参考答案: D 本题解释:D。所有人订一年半期刊所花的钱为（480＋420）元，则订了这份期刊的人数为（480＋420）＋[5×（6＋12）]＝10个人。

34、从一楼走到五楼，爬完一层休息30秒，一共要210秒，那么从一楼走到7楼，需要多少秒_____
A: 318B: 294C: 330D: 360
参考答案: C 本题解释:答案：C 解析：从一点走到五楼，休息了三次，那么每爬上一次需要的时间为（210-30×3）÷（5-1）=30秒，故从一楼走到七楼需要30×（7-1）+30×（7-2）=330秒。

35、任意取一个大于50的自然数，如果它是偶数，就除以2;如果它是奇数，就将它乘3之后再加1。这样反复运算，最终结果是多少?_____ B: 1C: 2D: 3
参考答案: B 本题解释:【答案】B。解析：此题可以用特值法，选择特殊值64，反复运算后得到最终结果为1。

36、152个球，放入若干个同样的箱子中，一个箱子最少放10个，最多放20个，且各个箱子的球数均不相同，问有多少种放法?(不计箱子的排列，即两种放法，经过箱子的重新排列后，是一样的，就算一种放法)_____
A: 1B: 7C: 12D: 24
参考答案: A 本题解释:A【解析】 设箱子个数为m，因为每只箱子的球数均不相同，最少放10个，最多放20个，所以m≤20-10+1=11。如果m=11，那么球的总数≥10×11+（0+1+2+…+10）=110+55>152，所以m≤10。如果m≤9，那么球的总数≤10×9+（10+9+8+…+2）=90+54=144<152，所以m=10在m=10时，10×10+（10+9+…+1）=155=152+3，所以一个箱子放10个球，其余箱子分别放11，12，14，15，16，17，18，19，20个球，总数恰好为152，而且符合要求的放法也只有这一种。故本题正确答案为A。

37、某服装店老板去采购一批商品，其所带的钱如果只买某种进口上衣可买120件，如果只买某种普通上衣则可买180件。现在知道，最后该老板买的进口上衣和普通上衣的数量相同，问他最多可以各买多少件?_____
A: 70B: 72C: 74D: 75
参考答案: B 本题解释:

38、地球表面的陆地面积和海洋面积之比是29︰71，其中陆地的四分之三在北半球，那么南、北半球海洋面积之比是_____
A: 284︰29B: 113︰55C: 371︰313D: 171︰113
参考答案: D 本题解释: 【解析】D。根据题干中的比例关系，可以推断出南、北半球的海洋面积之比为：

39、有14个纸盒，其中有装1只球的，也有装2只和3只球的。这些球共有25只，装1只球的盒数等于装2只球和3只球的盒数之和。装3只球的盒子有多少个?_____
A: 7B: 5C: 4D: 3
参考答案: C 本题解释: C【解析】设装有3只球的盒子有x个，装有2只球的盒子有y个，则装有1只球的盒子有（x+y）个。由题意可得：x+y+（x+y）=14（x+y）+3x+2y=25故x=4,y=3。

40、学校安排学生住宿，每个房间住6人还有2个空房间，如果每个房间住5人，则有1个房间里住的是3人，问：学校共有（ ）个房间?
A: 8B: 9C: 10D: 11
参考答案: C 本题解释:C【解析】假设学校有学生χ人，有房间y间，所以有6（y-2）=χ，5y-2=χ，由此可以得至χ=48，y=10。

41、混合并购是指一个企业对那些与自己生产的产品不同性质和种类的企业进行并购的行为，其中目标公司与并购企业既不是同一行业，又没有纵向关系。根据上述定义，下列属于混合并购的是_____。
A: 某碳酸饮料公司收购了一家灌装公司和一家饼干公司B: 某网站收购了一家户外传媒公司和一家网络游戏公司C: 某出版集团收购了一家印刷厂和一家文学网站D: 某电脑集团收购了一家酒厂和一家葡萄庄园
参考答案: D 本题解释:定义的关键信息是“目标公司与并购企业既不是同一行业，又没有纵向关系”。A项，灌装公司可以为饮料提供包装，因此和并购企业存在纵向关系，而饼干公司则和碳酸饮料公司都属于食品行业。B项，网站属于互联网传媒，因此网站和户外传媒属于同一行业；同时，网站也可能提供网络游戏，因此网站与网络游戏公司也可能存在纵向关系。C项，印刷是出版的一道流程，因此印刷厂和出版集团存在纵向关系。D项，酒厂和葡萄庄园虽然有可能存在纵向关系，但是二者与并购企业——电脑集团的产品性质完全不同，且不存在任何关系，因此选D。

42、一个班有50名学生，他们的名字都是由2个或3个字组成的。将他们平均分为两组之后，两组的学生名字字数之差为10。此时两组学生中名字字数为2的学生数量之差为_____。
A: 5B: 8C: 10D: 12
参考答案: C 本题解释:【解析】C。不定方程问题。由题意两组学生名字字数相差10，两边人数相同，即其中一组比另一组三名字人数多10人，则2名字人数少10人。

43、甲、乙两数之和加上甲数是220，加上乙数是170，甲、乙两数之和是多少_____
A: 50B: 130C: 210D: 390
参考答案: B 本题解释: 【解析】B。由题意可知，2甲+乙=220，甲+2乙=170，两式相加，即3（甲+乙）=390，所以甲+乙=130。

44、某原料供应商对购买其原料的顾客实行如下优惠措施：①一次购买金额不超过1万元，不予优惠;②一次购买金额超过1万元，但不超过3万元，给九折优惠;③一次购买金额超过3万元，其中3万元九折优惠，超过3万元部分八折优惠。某厂因库容原因，第一次在该供应商处购买原料付款7800元，第二次购买付款26100元，如果他一次购买同样数量的原料，可以少付：_____
A: 1460元B: 1540元C: 3780元D: 4360元
参考答案: A 本题解释:【解析】A。第一次购买原料付款7800元，原料的总价值应为7800元，第二次购买时付款26100元，原料的总价值应为26100&divide;0.9=29000元。如果要将两次购买变成一次购买，则总价值应为7800+29000=36800元，而应该付款额为30000&times;0.9+6800&times;0.8=32440元，一次性购买比分两次购买可以节约7800+26100-32440=1460元。

45、有4支队伍进行4项比赛，每项比赛的第一、第二、第三、第四名分别得到5、3、2、1分。每队的4项比赛得分之和算作总分，如果已知各队的总分不相同，并且A队获得了三项比赛的第一名，问总分最少的队伍最多得多少分? _____
A: 7B: 8C: 9D: 10
参考答案: B 本题解释:【答案】B 解析∶四项比赛的总得分是（5+3+2+1）×4=44分，A已得15分，最少得16分，剩下三人总得分最多为28分，要求得分最少的人得分最多且得分互不相同，则三人得分分别是8，9，11。此时一人得三项第二和一项第三，一人得一项第二和三项第三。

46、某市出租车收费标准是：5千米内起步费10.8元，以后每增加1千米增收1.2元，不足1千米按1千米计费。现老方乘出租车从A地到B地共支出24元，如果从A地到B地先步行460米，然后再乘出租车也是24元，那么从AB的中点C到B地需车费_____元。(不计等候时间所需费用)
A: 12B: 13.2C: 14.4D: 15.6
参考答案: C 本题解释:经济M题。共花钱24元，超过5千米的部分为24-10.8=13.2（元），超过5千米后走了13.2÷1.2=11（千米），总路程最多为16千米，因为步行460米后花费相同，说明460米后的路程一定超过15千米，则总路程15+0.46<S≤16，则C到B的距离7.73<< p>S/2≤8，因不足1千米按1千米计费，故应看成8千米，共花费10.8-9（8-5）×1.2=14.40（元）。

47、甲、乙两人在一条环形跑道散步，两人从同一点A出发，背向而行。已知甲每分钟步行50米，乙每分钟步行30米，两人第一次在B点相遇，相遇后继续以原来的速度前进，第二次相遇在C点。若B、C两点沿环形跑道的较短距离为150米，则环形跑道的长度为多少米？_____
A: 400B: 450C: 560D: 600
参考答案: A 本题解释:【答案】A。解析：设环形跑道的长度为8x，甲、乙两人的速度比为5：3，则第一次相遇时，甲走的路程为5x、乙走的路程为3x；从第一次相遇到第二次相遇，甲的路程仍然是5x、乙的路程仍然是3x，可得3x＝150，解得x＝50。则环形跑道的长度为80×5＝400（米）。因此，本题选择A选项。

48、某店原来将一批苹果按100%的利润(即利润是成本的100%)定价出售，由于定价过高，无人购买，后来不得不按38%的利润重新定价，这样出售了其中的40%。此时，因害怕剩余水果腐烂变质，不得不再次降价，售出了剩余的全部水果。结果，实际获得的总利润是原定利润的30.2%，那么第二次降价后的价格是原定价的_____。
A: 75%B: 50.%C: 62.5%D: 45%
参考答案: C

49、有20名工人修筑一段公路，计划15天完成。动工3天后抽出5人去其他工地，其余人继续修路。如果每人工作效率不变，那么修完这段公路实际用_____
A: 19天B: 18天C: 17天D: 16天
参考答案: A 本题解释:【答案】A。解析：5人12天完成的工作量分配给15人需要5×12÷15=4天完成，所以修完这段公路实际用15+4=19天。

50、某考试均为判断题,共10题,每题10分,满分为100分。考生答题时认为正确则画为“0”。认为不正确则画“×”。以下是考生的答题情况及甲、乙、丙的实际得分,则丁的得分为_____。题号12345678910得分甲××0×0××0××0乙×000×0×0000丙×000×××0×00丁××000××0000
A: 20分B: 40分C: 60分D: 80分
参考答案: C 本题解释:【答案】C。解析:首先观察甲和丙，得分相差40分，而他们的答案不一样的出恰好有4题，那么也就是说，丙和甲不一样的题(即2，4，5，10)甲都做对了，而这四道题恰好乙也全做错了，而乙一共做错了5道题，也就是说剩下的题目(1，3，7，8，6，9)中，乙只错了一个;又四人判断一致的题目，(即1，3，7，8)中必有一个四个人全做错了，因为丙一共只做对了3道题，那么，也就是说6、9、题乙做对了，那么现在答案除了1、3、7、8都确定了，即(2，4，5，10)与甲一致，(6，9)与乙一致,在这6道题中丁做对了3道,剩下的(1,3,7,8)丁做对3道。综上所述,丁得分60分。

51、商店卖气枪子弹，每粒1分钱，每粒4分钱，每10粒7分钱，每20粒1角2分钱。小明的钱至多能买73粒，小刚的钱至多能买87粒.小明和小刚的钱合起来能买多少粒? _____
A: 160B: 165C: 170D: 175
参考答案: B 本题解释: 【答案】B。解析：小明子弹73颗，可知买了3个20粒，1个10粒，3个1粒，共有46分钱;同理小刚买了4个20粒，1个5粒，2个l粒，共有54分钱。两人共有100分钱，可以买8个20粒，1个5粒，共卖165粒。

52、有黑、白、黄色袜子各10只，不用眼睛看，任意地取出袜子来，使得至少有两双袜子不同色，那么至少要取出_____只袜子。
A: 12 B: 13C: 11 D: 14
参考答案: B 本题解释:B 【解析】考虑最坏的情形，把某一种颜色的袜子全部先取出，然后，在剩下两色袜子中各取出一只，这时再任意取一只都必将有两双袜子不同色，即10+2+l=13（只）。故选B。

53、小明用5天时间看完了一本200页的故事书。已知第二天看的页数比第一天多,第三天看的页数是第一、二两天看的页数之和，第四天看的页数是第二、三两天看的页数之和，第五天看的页数是第三、四两天看的页数之和。那么小明第五天至少看了_____页。
A: 84B: 78C: 88D: 94
参考答案: A 本题解释:【答案】A。解析：设小明第一天看了a页，第二天看了b页,则前五天看的页数依次为a，b，a+b，a+2b，2a+3b。这些数的和是200，可得5a+7b=200。因为5a与200都是5的倍数，所以b是5的倍数。因为ba，所以上式只有两组解b=20，a=12；b=25，a=5。将这两组解分别代入2a+3b，得到第五天至少看了84页。

54、甲用1000元人民币购买了一手股票，随即他将这手股票转卖给乙，获利10％，乙而后又将这手股票返转卖给甲，但乙损失了10％，最后甲按乙卖给自己的价格的九折将这手股票又卖给了乙，则在上述股票交易中_____。
A: 甲刚好盈亏平衡DB: 甲盈利1元C: 甲盈利9元D: 甲亏本1.1元
参考答案: B 本题解释:【答案】B。解析：甲第一次将股票以1000×（1+10%）=1100元转卖给乙，盈利100元，乙又以1100×（1-10%）=990元转卖给甲，甲又以990×0.9=891元转卖给乙，则甲共盈利100-990+891=1元，故本题选择B。

55、篮球规则中得分有3分，2分，1分，若在一次比赛中，队员A一人得了13分，那么他的得分组合共_____种。
A: 18　B: 19　C: 20　D: 21
参考答案: D 本题解释:D[解析]当A 的3分分别拿到4，3，2，1，0次的时候，对应的组合数分别是1，3，4，6，7，所以A的得分组合共有1+3+4+6+7=21种，选D。

56、一列队伍沿直线匀速前进，某时刻一传令兵从队尾出发，匀速向队首前进传送命令，他到达队首后马上原速返回，当他返回队尾时，队伍行进的距离正好与整列队伍的长度相等。问传令兵从出发到最后到达队尾所行走的整个路程是队伍长度的多少倍？_____
A: 0.5 B: 1.5C: 1 D: 2
参考答案: C 本题解释:【答案】C。解析：从队尾到队首，这是一个追及过程，追及的路程等于队伍的长。从队首返回队尾，这是一个相遇过程，返回队尾所行的路程都等于队伍的长。

57、某单位有60名运动员参加运动会开幕式，他们着装白色或黑色上衣，黑色或蓝色裤子。其中有12人穿白上衣蓝裤子，有34人穿黑裤子，29人穿黑上衣，那么穿黑上衣黑裤子的有多少人? _____
A: 12B: 14C: 15D: 19
参考答案: C 本题解释:C。【解析】有34人穿黑裤子，则有60-34=26个人穿蓝色裤子，26-12=14个人穿黑衣蓝裤，则有29-14=15个人穿黑衣黑裤

58、小王的手机通讯录上有一手机号码，只记下前面8个数字为15903428。但他肯定，后面3个数字全是偶数，最后一个数字是6，且后3个数字中相邻数字不相同，请问该手机号码有多少种可能?_____
A: 15B: 16C: 20D: 185
参考答案: B 本题解释:【答案】B。解析：一位偶数有0、2、4、6、8，共5个。考虑倒数第二位，因为相邻数字不相同且为偶数，则有4种选择。倒数第三位与倒数第二位不相同，也有4种选择，共有4×4=16种情况。

59、林文前年买了8000元的国家建设债券，定期3年。到期他取回本金和利息一共10284.8元。这种建设债券的年利率是多少？_____
A: 9.52% B: 9.6% C: 8.4% D: 9.25%
参考答案: A 本题解释:A【解析】求利息的公式：利息=本金×利率×时间，可得出：利率=利息÷时间÷本金。而他3年所得的利息是：10284.8-8000=2284.8（元）；这样即可求出这债券的年利率是多少。（10284.8-8000）÷3÷8000=2284.8÷3÷8000=761.6÷8000=0.0952=9.52%

60、A、B、C、D、E，5个小组开展扑克牌比赛，每两个小组之间都要比赛一场，到现在为止，A组已经比赛了4场，B组已经比赛了3场，C组已经比赛了2场，D组已经比赛了1场，问E组已经比赛了几场（）
A: oB: 1C: 2D: 3
参考答案: C 本题解释:C【解析】A组已经比赛了4场，说明A组与B、C、D、E这4个组都进行过比赛;D组已经比赛了1场，则根据上一个条件，D组只与A组进行过比赛;B组已经比赛了3场，则根据上一个条件，B组只与A、C、E组进行过比赛;C组已经比赛了2场，则根据上面的条件，C组只能与A、B组进行过比赛;所以E组与A、B组进行过比赛。

61、某单位有宿舍11间，可以住67人，已知每间小宿舍住5人，中宿舍住7人，大宿舍住8人，则小宿舍间数是_____。
A: 6B: 7C: 8D: 9
参考答案: A 本题解释:【答案】A。解析：设小宿舍有x间，中宿舍有y间，大宿舍有11-x-y间。依题意5x+7y+8（11-x-y）=67，得到3x+y=21。〔化为标准形式〕因为x、y均是大于0的整数，所以x＜7。直接选A。〔确定解的范围〕

62、筑路队原计划每天筑路720米，实际每天比原计划多筑路80米，这样在规定完成全路修筑任务的前3天，就只剩下1160米未筑，这条路全长多少千米?_____
A: 8.10B: 10.12C: 11.16D: 13.50
参考答案: C 本题解释: C解析：现在每天筑路：720+80=800（米）规定时间内，多筑的路是：（720+80）×3-1160=2400-1160=1240（米）求出规定的时间是1240÷80=15.5（天），这条路的全长是720×15.5=11160（米）。故本题选C。

63、有一根长240米的绳子，从某一端开始每隔4米作一个记号，每隔6米也作一个记号。然后将标有记号的地方剪断，则绳子共剪成_____段。
A: 40B: 60C: 80D: 81
参考答案: C 本题解释:【答案】C。解析：容斥原理，每隔4米作一个记号，则作记号数为240÷4－1＝59；每隔6米作一个记号，则作记号数为240÷6－1＝39；其中每隔12米的记号重复被作两次，类似的记号数为240÷12－1＝19。因此做记号总数为59＋39－19＝79，即绳子被剪成80段。故正确答案为C。两集合容斥原理公式：|A∪B|＝|A|＋|B|－|A∩B|

64、某公交线路从起点到终点共25个站点，每天早上6点分别从起点站和终点站同时发出首班车，晚上10点开出末班车，每班车发车时间间隔10分钟。假设每辆车从一个站点行驶到下一个站点所需时间为5分钟，则该线路至少需要配备_____辆车。
A: 24B: 13C: 12D: 26
参考答案: A 本题解释:【答案】A。解析：25个车站，一共有24段，每段是5分钟，所以一辆车从最开始至最末端是24×5=120分钟，120÷10=12辆车，因为是在两端发车，所以车辆的数量为24辆。因此，本题答案为A选项。

65、19991998的末位数字是：_____
A: 1 B: 3 C: 7 D: 9
参考答案: A 本题解释:【解析】此题关键是要考察末位数的变化情况，9的一次幂、二次幂、三次幂、四次幂……的尾数呈9、1、9、1……变化，即其奇数次幂时尾数是9，偶数次幂时尾数是1，所以，选A

66、某种灯泡出厂售价为6.2元，采用新的生产技术后可节约12％的成本，若售价不变，利润可比原来增长50％。问该产品最初的成本为多少元？_____
A: 3.8B: 4.5C: 5.0D: 5.5
参考答案: C 本题解释:【答案】C。解析：设原来的成本为x元，那么6.2一0.88x=（1+0.5）（6.2一x），解得x=5。故选C。

67、林文前年买了8000元的国家建设债券，定期3年。到期他取回本金和利息一共10284.8元。这种建设债券的年利率是多少?_____
A: 9.52%B: 9.6%C: 8.4%D: 9.25%
参考答案: A 本题解释:A。【解析】求利息的公式：利息=本金×利率×时间，可得出：利率=利息÷时间÷本金。而他3年所得的利息是：10284.8-8000=2284.8（元）;这样即可求出这债券的年利率是多少。（10284.8-8000）÷3÷8000=2284.8÷3÷8000=761.6÷8000=0.0952=9.52%。

68、下列可以分解为三个质数相乘的最小的三位数是_____。
A: 100B: 102C: 104D: 105
参考答案: B 本题解释:【答案】B。解析：直接代入各选项求解。题目要求找出符合条件的最小的三位数，则从数值较小的选项开始验证。A项，100＝2×2×5×5，不符合题意。B项，102＝2×3×17，符合题意。C、D项的三位数即使可分解为三个质数相乘，数值上也大于B项的102，因此不作考虑。故正确答案为B。

69、有100人参加运动会的三个比赛项目，每人至少参加一项，其中未参加跳远的有50人，未参加跳高的有60人，未参加赛跑的有70人。问至少有多少人参加了不止一个项目?_____
A: 7B: 10C: 15D: 20
参考答案: B 本题解释:B【解析】最值问题。由题意，参加跳远的人数为50人，参加跳高的为40人，参加赛跑的为30人;即参加项目的人次为120人次;故欲使参加不止一项的人数最少，则需要使只参加一项的人数最多为x，参加3项的人数为y;故x+3y=120，x+y=100，解得y=10。

70、两排蜂房，一只蜜蜂从左下角的1号蜂房到8号蜂房，假设只向右方(正右或右上或右下)爬行，则不同的走法有_____。
A: 16种B: 18种C: 21种D: 24种
参考答案: C 本题解释:

71、某月刊每期定价5元。某单位一部分人订半年，另一部分人订全年，共需订费480元；如果订半年的改订全年，订全年的改订半年，那么共需420元。共有多少人订了这份期刊？_____
A: 25B: 20C: 15D: 10
参考答案: D 本题解释:D。所有人订一年半期刊所花的钱为（480＋420）元，则订了这份期刊的人数为（480＋420）＋[5×（6＋12）]＝10个人。

72、商场的自动扶梯以匀速由下往上行驶，两个孩子嫌扶梯走得太慢，于是在行驶的扶梯上，男孩每秒钟向上走2个梯级，女孩每2秒钟向上走3个梯级。结果男孩用40秒钟到达，女孩用50秒钟到达。则当该扶梯静止时，可看到的扶梯梯级有_____。
A: 80级 B: 100级 C: 120级 D: 140级
参考答案: B 本题解释:B。【解析】男孩所走的台阶数为40×2=80，女孩所走的台阶数为50/2×3=75，那么电梯的速度就应该为（80-75）/（50-40）=0.5，电梯所经过的台阶就为40×0.5=20， 电梯经过的台阶加上男孩经过的台阶，就是电梯的台阶数，即100级。

73、心灵投射谬误也称为投射作用，它是一种非形式谬误，有两种形式，一种形式是某人认为他看世界的观点反映了世界的真相。也就是，某人将他的个人感觉投射到真实世界；另一种形式是某人认为自己不了解一个现象意味着这现象无法被理解或不是真的。根据上述定义，下列不属于心灵投射谬误的是_____。
A: 小李忍受不了闻臭豆腐的味道，就说臭豆腐这么臭，没人会喜欢吃B: 小敏是重庆人，到上海工作后，他发现上海菜普遍是甜的，于是他逢人就说上海菜很难吃C: 尽管知道葡萄架上的葡萄很甜，但是小刘因为摘不到，就对别人说葡萄很酸D: 课间，小荣给大家讲了一个冷笑话，小明理解不了为什么大家听后都捧腹大笑，就说小荣讲的笑话一点水平都没有
参考答案: C 本题解释:【答案】C。解析：心灵投射谬误有两种形式，一种是强调自己的主观意识，即认为自己的观点就是事情的真相。另一种认为自己不了解的就是无法理解的或不是真的。C项小刘的行为是自欺欺人的表现，他对别人说葡萄很酸，但自己并没有认为葡萄是酸的，因为他知道葡萄很甜，不符合“心灵投射谬误”的定义，故本题选C。

74、n为100以内的自然数，那么能令2n-1被7整除的n有多少个?_____
A: 32B: 33C: 34D: 35
参考答案: B 本题解释:答案：B.[解析]当n是3的倍数的时候，2n-1是7的倍数。也就是求100以内3的倍数，从3到99，共有33个。故选B。

75、甲、乙沿同一公路相向而行，甲的速度是乙的1.5倍，已知甲上午8点经过邮局，乙上午10点经过邮局。问：甲乙在中途何时相遇? _____
A: 8点48分B: 8点30分C: 9点D: 9点10分
参考答案: A 本题解释:A。【解析】设乙的速度为x，甲就是1.5x，当甲8点到邮局时，乙离邮局还有2个小时的路程（2x），甲乙走完2x路程需要2x/（1.5x+x）=4/5小时=48分钟，加上8点，就是8点48分相遇。

76、现有一个无限容积的空杯子，先加入1克酒精，再加入2克水，再加入3克酒精，再加入4克水，&hellip;&hellip;，如此下去，问最终杯子中酒精溶液浓度为多少?_____ B: 25%C: 33.3%D: 50%
参考答案: D 本题解释:【解析】D。如果把加一次酒精和水看成一个流程，则经过n个流程后，杯子里面有1+3+5+&hellip;+(2n-1)=1/2n(1+2n-1)=n2克酒精，而酒精溶液有1+2+&hellip;+2n=1/2&times;2n(1+2n)=n(1+2n)克。故此时酒精溶液浓度为n2/n(1+2n)=n/(2n+1)，当n趋于无穷大时，溶液浓度趋于1/2=50%。思路点拨：极端法，当加入酒精或水的量极大时连续两次操作水与酒精的差距对整体的影响可以忽略不计，因此必然各占50%。

77、某数的百分之一等于0.003，那么该数的10倍是多少?_____。
A: 0.003B: 0.03C: 0.3D: 3
参考答案: D 本题解释:D【解析】某数的百分之一为0.003，则该数为0.3，那么它的10倍为3。故正确答案为D。

78、有一个长方体容器，长40厘米，宽30厘米，高10厘米，里面的水深6厘米(最大面为底面)。如果把这个容器盖紧，再竖起来(最小面为底面)，则里面的水深是多少厘米_____
A: 15厘米 B: 18厘米 C: 24厘米 D: 30厘米
参考答案: C 本题解释:【解析】C。盖紧后竖起前水的底面积为40×30平方厘米，深为6厘米，则体积为40×30×6立方厘米。盖紧后竖起水的体积不变，底面积变成了30×10平方厘米，此时水深应为。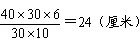

79、某车间三个班组共同承担-批加工任务，每个班组要加工100套产品。因为加工速度有差异，一班组完成任务时二班组还差5套产品没完成，三班组还差10套产品没完成。假设三个班组加工速度都不变，那么二班组完成任务时，三班组还剩_____套产品未完成。
A: 5 B: 80/19 C: 90/19 D: 100/19
参考答案: D 本题解释:D。工程问题。相同的时间内，一班组完成了100套，二班组加工了100-5=95（套），三班组加工了100-10=90（套），因此二班组、三班组的效率比为95∶90。当二班组完成任务时，即加工了100套，设此时三班组加工了x套，有95∶90=100∶x，得到x=1800/19。因此未完成的为100-1800/19=100/19（套）。

80、教室里有若干学生，走了10名女生后，男生是女生人数的2倍，又走了9名男生后，女生是男生人数的5倍。问：最初有多少名女生?_____
A: 15B: 12C: 10D: 9
参考答案: A 本题解释:A【解析】设最初有x名女生，则男生的数量为2(x-10)，由题意可列等式x-10=5[2(x-10)-9]，可得x=15。故选A。

81、123456788×123456790-123456789×123456789=_____。
A: 0B: 1C: 2D: -1
参考答案: D 本题解释: D [解析] 原式=（123456789-1）×（123456789+1）-1234567892=1234567892-1-1234567892=-1故选D。

82、银行整存整取的年利率是：2年期为2.25%，3年期为2.52%，5年期为2.79%，如果甲、乙二人同时各存入1万元，甲先存2年期，到期后连本带利改存为3年期;乙存5年期。5年后，2人同时取出，那么两人的收益差为多少元?_____
A: 64B: 102C: 155D: 234
参考答案: C 本题解释:C【解析】 甲5年后取出本利和为：10000×（1+2.25%×2）×（1+2.52%×3）=10000×1.045×1.0756=11240（元）乙5年后取出本利和为：10000×（1+2.79%×5）=1000×1.1395=11395由此可见，乙的收益多。11395-11240=155（元）。故选C。

83、孙某共用24000元买进甲、乙股票若干，在甲股票升值15%、乙股票下跌10%时全部抛出，共赚到1350元，则孙某最初购买甲、乙两支股票的投资比例是_____。
A: 5∶3 B: 8∶5 C: 8∶3 D: 3∶5
参考答案: A 本题解释:A。经济利润问题。设甲股票买了X元，乙股票买了Y元，列方程组：X+Y=2400015%X-10%Y=1350解得X=15000，Y=9000，故X∶Y=15∶9=5∶3, 选A。

84、王师傅在某个特殊岗位上工作，他每上8天班后，就连续休息2天。如果这个星期六和星期天他休息，那么，至少再过几个星期后他才能又在星期天休息?_____
A: 7个B: 10个C: 17个D: 70个
参考答案: A 本题解释:【解析】设至少过N个星期，可能第N个星期六与星期日连续休息，也可能第N个星期天与星期一连休2天，前者得出：7N-2=10K+8………………（1）后者得出7N-1=10K+8………………（2）其中K是自然数，由（1）得7N=10（K+1），因此，7N是10的倍数，N最小为10。由（2）得7N=10K+9，表明7N的个位数字是9，所以N=7，17，…。可见，至少再过7个星期后，才能又在星期天休息。故本题正确答案为A。

85、由1、2、3组成的没有重复数字的所有三位数之和为多少？_____
A: 1222 B: 1232 C: 1322 D: 1332
参考答案: D 本题解释:D。因为1、2、3之和可被3整除，故而1、2、3所组成的没有重复数字的三位数都能被3整除，而这些数字相加之和也必能被3整除，只有D项能被3整除，为正确答案。根据排列组合原理，可知该没有重复数字的三位数共有6个，1、2、3三个数在个、十、百位上各出现两次，即（1+2+3）×2=12，也就是说这一数字当为12+120+1200=1332。

86、某区要从10位候选人中投票选举人大代表，现规定每位选举人必须从这10位中任选两位投票，问至少要有多少位选举人参加投票，才能保证有不少于10位选举人投了相同两位候选人的票?_____
A: 382位B: 406位C: 451位D: 516位
参考答案: B 本题解释:【答案】B。解析：从10位候选人中选2人共有种票，则每种票有9张相同时需要×9=405个人投票，那么只需要再加一人可以保证有不少于10人投了相同两位候选人的票。

87、甲从某地匀速出发，一段时间后，乙从同一地点以同样的速度同向前进，在K时刻乙距离起点30米，当乙走到甲在K时刻的位置时，甲离起点108米，问，此时乙距起点多少米?_____
A: 39B: 69C: 78D: 138
参考答案: B 本题解释:正确答案：B解析：本题属于路程问题。K时刻之后，甲、乙走过的距离相等。若K时刻后，乙走过的距离为X，则2X+30=108解得X=39。此时乙和起点的距离为：30+39=69米。本题画线段图，可直接解出。故答案为B。

88、如果甲比乙多20%，乙比丙多20%，则甲比丙多百分之多少?_____
A: 44B: 40C: 36D: 20
参考答案: C 本题解释:答案：C【解析】这道题实际只要考虑五个五个一数最后剩一个，三个三个一数最后剩一个，即可。这两个最好思考。只有501与421一幕了然，除以5余1。而501能被3整除，只有42。

89、某商品按定价的80%(八折)出售，仍能获得20%的利润，问定价时期望的利润率是多少?_____
A: 50%B: 40%C: 30%D: 20%
参考答案: A 本题解释:【答案解析】设成本为1，根据定价的80%=1.2，所以定价为1.5，1.5-1=0.5，选A。考查对于利润的理解：单个商品利润=售价-成本，获得百分之几的利润是相对于成本来说的，如我们生产一支笔成本1元，我们将它以1.5元出售，则获得利润为0.5元，因为(0.5/1)*100%=50%，所以获得了50%的利润解法如下：设定价为y，成本为x，则按定价80%出售，仍获得20%利润用数学公式表示就是0.8y-x=0.2x，即售价-成本=利润因此，得y=3x/2，或按原价出售，则利润为，y-x=3x/2-x=x/2即利润率为50%。

90、有红、黄、蓝、白珠子各10粒，装在一只袋子里，为了保证摸出的珠子有两粒颜色相同，应至少摸出几粒？_____
A: 3B: 4C: 5D: 6
参考答案: C 本题解释:【答案】C。解析：抽屉原理问题，利用最不利原则解题。题目要求“两粒颜色相同”，“最不利”的情况就是每种颜色都只摸出来一粒，即从口袋中取出红、黄、蓝、白珠子各1粒，即取出4粒球后，再取出一粒珠子，就必有两粒颜色相同。因此，至少取出4+1=5粒才能保证摸出的珠子中有两粒的颜色相同。因此，本题答案选择C选项。

91、一只油轮从甲港顺流而下到乙港，马上又逆水返回甲港，共用8小时，顺水每小时比逆水每小时多行12千米，前4小时比后4小时多行30千米，则甲、乙两港相距_____千米。
A: 72B: 60C: 55D: 48
参考答案: C 本题解释:【解析】由于顺水速度大于逆水速度。且顺水、逆水的行程相等，则顺水时间小于逆水时间，后4/小时全是逆水，前4小时先是顺水后是逆水，顺水时间=30÷12=2.5小时，逆水时间=8-2.5=5.5/小时，故顺水速度：逆水速度=5.5：2.5=11：5，顺水速度=12÷（11.-5）×11=22千米/时，两港距离=22×2.5=55（千米）。故选C。

92、用2、4、5、7这4个不同数字可以组成24个互不相同的四位数，将它们从小到大排列，那么7254是第多少个数?_____
A: 19B: 20C: 18D: 17
参考答案: B 本题解释:【解析】由已知得每个数字开头的数各有24÷4=6个，从小到大排列，7开头的从第6×3+1=19个开始，易知第19个是7245，第20个是7254。

93、甲、乙两人进行乒乓球比赛，比赛采取三局两胜制，无论哪一方先胜两局则比赛结束。甲每局获胜的概率为2/3，乙每局获胜的概率为1/3。问甲最后取胜的概率是多少?_____
A: AB: BC: CD: D
参考答案: A

94、某公司采取百分制对员工进行绩效考核，在12月的考核中，男员工的平均分数为80分，女员工的平均分数为84.25分，而全公司的平均分数为82.5分，如果该公司员工人数多于80人而小于90人，那么该公司男员工和女员工的人数分别为多少？_____
A: 35、50B: 50、35C: 40、45D: 45、40
参考答案: A 本题解释:A。

95、有8种颜色的小球,数量分别为2、3、4、5、6、7、8、9，将它们放进一个袋子里面，问拿到同颜色的球最多需要几次?_____
A: 6B: 7C: 8D: 9
参考答案: D 本题解释:【答案解析】解析："抽屉原理"问题。先从最不利的情况入手，最不利的情况也就使次数最多的情况。即8种小球，每次取一个，且种类不相同(这就是最不利的情况)。然后任取一个，必有重复的，所以是最多取9个。

96、一段路程分为上坡、平路、下坡，三段路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米，路程全长是50千米，小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A

97、一条街上，一个骑车人和一个步行人相向而行，骑车人的速度是步行人的3倍，每个隔10分钟有一辆公交车超过一个行人。每个隔20分钟有一辆公交车超过一个骑车人，如果公交车从始发站每隔相同的时间发一辆车，那么间隔几分钟发一辆公交车？_____
A: 10B: 8C: 6D: 4
参考答案: B 本题解释:B。【解析】设车速V车，人速V人，自行车速3V人，则（V车－V人）×10＝20×（V车－3V人），V车＝5V人，即车走人4倍位移追上人故T＝4×V人×10/5V人＝8。

98、有两根长短粗细不同的蚊香，短蚊香可燃8小时，长蚊香可燃的时间是短蚊香的1/2，同时点燃两根蚊香，经过3小时，它们的长短正好相等，未点燃之前，短蚊香比长蚊香短_____。
A: 1/6B: 1/5C: 1/2D: 3/5
参考答案: D 本题解释:D【解析】两根蚊香同时点燃3小时后所剩长度相等，从这里我们可以找出长、短蚊香的长度关系：短蚊香点燃3小时后剩1-1× 3/8=5/8，长蚊香点燃3小时后剩1-（1×3）/（8×1/2）=1/4，即短蚊香的5/8等于长蚊香的1/4，由此可求出短蚊香是长蚊香的几分之几，即5/8短=1/4长，短/长=2/5，所以未点燃之前，短蚊香比长蚊香短1-2/5=3/5。

99、红星小学组织学生排成队步行去郊游,每分钟步行60米,队尾的王老师以每分钟步行150米的速度赶到队头,然后立即返回队尾,共用10分钟。求队伍的长度。_____
A: 630米B: 750米C: 900米D: 1500米
参考答案: A 本题解释:【答案】A。解析:设王老师从队尾走到队头用x分钟,可列方程(150-60)×x=(150+60)×(10-x),解得x=7分钟,则队伍的长度为(150-60)×7=630米,选择A。

100、用0，1，2，…，9这10个数字组成一个四位数，一个三位数，一个两位数与一个一位数，每个数字只许用一次，使这四个数的和等于2007，则其中三位数的最小值为_____。
A: 386B: 260C: 230D: 204
参考答案: D 本题解释:D。