1、甲从某地出发匀速前进,一段时间后,乙从同一地点以同样的速度同向前进,在K时刻乙距起点30米;他们继续前进,当乙走到甲在K时刻的位置时,甲离起点108米。问:此时乙离起点多少米?_____
A: 39米B: 69米C: 78米D: 138米
参考答案: B 本题解释:正确答案是B考点行程问题解析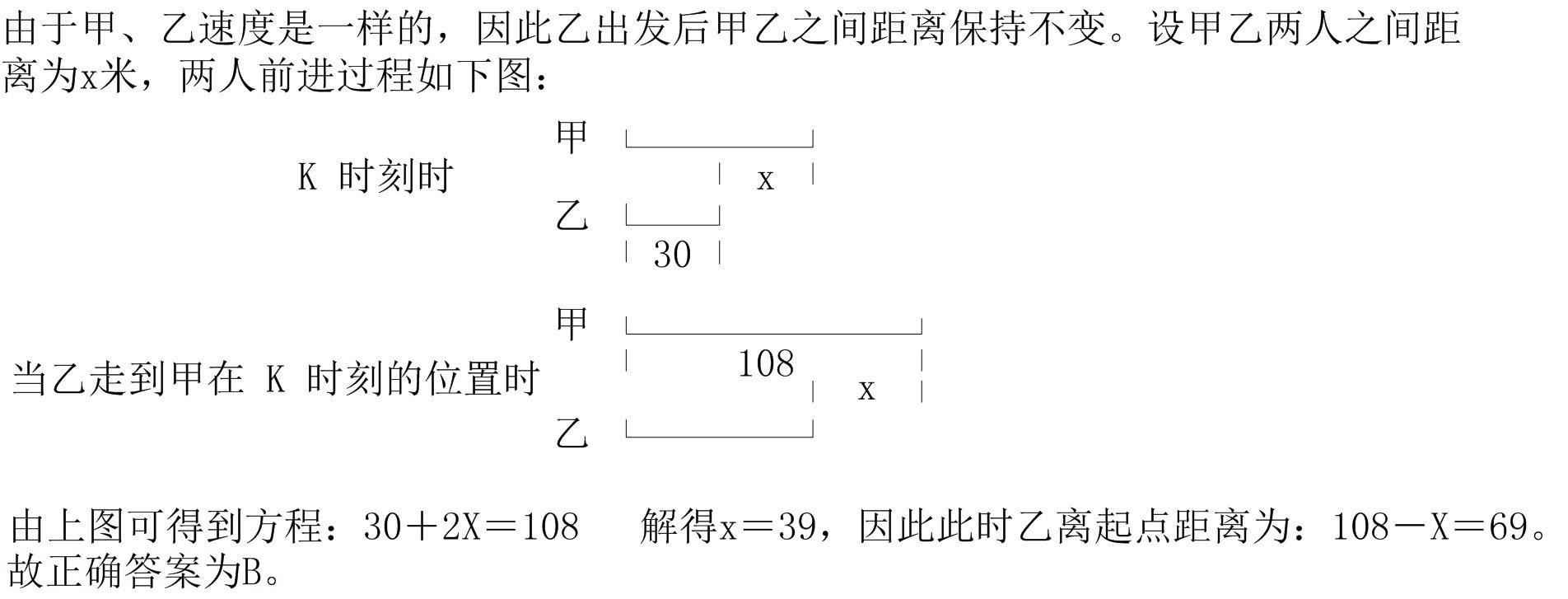 标签画图分析
标签画图分析
2、某试卷共25题,答对的,一题得4分;答错或不答的,一题扣1分,小王得了60分,则小王答对了多少题?_____
A: 14B: 15C: 16D: 17
参考答案: D 本题解释: D [解析] 设答对了x道题,则未答对的题为(25-x)题,可得4x-(25-x)×1=60,解得x=17。故本题选D。
3、 _____
_____
A: AB: BC: CD: D
参考答案: A 本题解释:正确答案是A考点趣味数学问题解析设空白图案为a,交叉图案为b,钟表图案为c,故可得如下:a+c×3=a×2+b×2,a+b×2=c×2+a×3,解得c=3a,b=4a;则可得a×2+b=6a=2c,故正确答案为A。
4、某一地区在拆迁时将一些枯死的树木刨出。拆迁办组织三个部门的人员准备将树木锯成短木,树木的粗细都相同,只是长度不一样。甲部门的人锯的树木是2米长,乙部门的人锯的树木是1.5米长。丙部门的人锯的树木是1米长,都要求按0.5米长的规格锯开。时间结束时,三个部门正好把堆放的树木锯完,张三那个部门共锯了27段,李四那个部门共锯了28段,王五那个部门共锯了34段。请问,张三属于哪个部门的?_____
A: 属于丙部门,甲部门最慢B: 属于乙部门,丙部门最慢C: 属于甲部门,丙部门最慢D: 属于乙部门,乙部门最慢
参考答案: B 本题解释:参考答案:B题目详解:张三部门27段=13.5米李四部门28段=14米王五部门34段=17米由于树木都是整根的张三部门一共锯了13.5米所以他们的树木只能是1.5米长的,所以张三是乙部门的。2相对应的王五部门17米长不可能是2米长的只能是1米长的木头,王五是丙部门的。3剩下的李四部门的木头都是2米长的,李四是甲部门的。13.5米=9根木头每根木头锯2次一共是锯了18次;14米=7跟木头每根木头锯3次一共锯了21次;17米=17根木头每根木头锯一次一共锯了17次。所以丙部门最慢。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除特征
5、某高校从E、F和G三家公司购买同一设备的比例分别是20%、40%和40%,E、F和G三家公司所生产设备的合格率分别是98%、98%和99%,现随机购买到一台次品设备的概率是_____。
A: 0.013B: 0.015C: 0.016D: 0.01
参考答案: C 本题解释:正确答案是C考点概率问题解析买到次品的概率为20%×2%+40%×20%+40%×1%=0.016,故正确答案为C。
6、工作人员做成了一个长60厘米,宽40厘米,高22厘米的箱子,因丈量错误,长和宽均比设计尺寸多了2厘米,而高比设计尺寸少了3厘米,那么该箱子的表面积与设计时的表面积相差多少平方厘米?_____
A: 4B: 20C: 8D: 40
参考答案: C 本题解释:正确答案是C考点几何问题解析实际表面积为(60×40+40×22+60×22)×2,设计表面积为(58×38+38×25+58×25)×2,计算尾数,实际表面积尾数为0,设计表面积尾数为(4+0+0)×2=8,二者之差尾数为2或8,显然只有C符合条件。故正确答案为C。
7、连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米,则正八面体的体积为_____立方厘米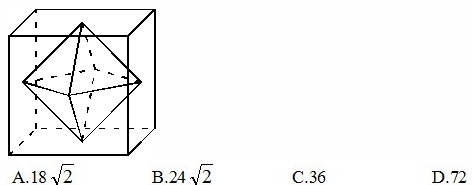
A: AB: BC: CD: D
参考答案: C 本题解释:正确答案是C考点几何问题解析 秒杀技该正八面体可看成上下两个正四棱锥组成,注意到每个四棱锥的底面面积为正方体底面面积的一半,每个四棱锥的高为立方体棱长的一半,因此可知每个四棱锥的体积为正方体体积的1/12,故该正八面体体积为正方体体积的1/6,于是其体积为1/6×6^3=36。
秒杀技该正八面体可看成上下两个正四棱锥组成,注意到每个四棱锥的底面面积为正方体底面面积的一半,每个四棱锥的高为立方体棱长的一半,因此可知每个四棱锥的体积为正方体体积的1/12,故该正八面体体积为正方体体积的1/6,于是其体积为1/6×6^3=36。
8、某班共有50名学生参加数学和外语两科考试,已知数学成绩及格的有40人,外语成绩及格的有25人,据此可知数学成绩及格而外语成绩不及格者_____。
A: 至少有10人B: 至少有15人C: 有20人D: 至多有30人
参考答案: B 本题解释:答案:B【解析】这是一个集合问题,首先可排除答案D,因为与已知条件“外语及格25人”即“外语不及格25人”不符;其次排除C,因为仅以外语及格率为50%推算数学及格者(40人)中外语不及格人数为40×50%=20(人),缺乏依据,实际上,数学及格者中外语不及格的人数至少为25-(50-40)=15人,答案为B。
9、“红星”啤酒开展“7个空瓶换l瓶啤酒”的优惠促销活动。现在已知张先生在活动促销期问共喝掉347瓶“红星”啤酒,问张先生最少用钱买了多少瓶啤酒?_____
A: 296B: 298C: 300D: 302
参考答案: B 本题解释:由题可知,6个空瓶可以换一个瓶子里面的啤酒,298÷6=49……4,只有49+298=347。
10、一个四位数”□□□□”分别能被15、12和10除尽,且被这三个数除尽时所得的三个商的和为1365,问四位数”□□□□”中四个数字的和是_____。
A: 17B: 16C: 15D: 14
参考答案: C 本题解释:正确答案是C考点计算问题解析列方程可解得,设4位数为X,有X/15+X/12+X/10=1365,解得X=5460,4数字和为15。故正确答案为C。秒杀技由题意可知,该四位数能被3整除,则其所有数字之和能被3整除,仅C符合。标签数字特性
11、张家和李家都使用90米的篱笆围成了长方形的菜园,已知李家的长方形菜园的长边比张家短5米,但是菜园面积却比张家大50平方米,则李家的长方形菜园面积为_____。
A: 550平方米B: 500平方米C: 450平方米D: 400平方米
参考答案: B 本题解释:【答案】B。解析:缺少的量为张家和李家菜园的具体长宽,可用方程法。设李家菜园长边为x米,则其短边长为45-x米;张家菜园长边为x+5米,其短边长为40-x,根据题意:x(45-x)-(x+5)×(40-x)=50,可解得x=25,李家菜园面积为x(45-x)=25×20=500。故本题答案为B选项。
12、1/3+1/15+1/35+1/63+1/99+1/143+1/195+1/255的值是_____。
A: 6/17B: 6/19C: 8/17D: 8/19
参考答案: C 本题解释:正确答案是C考点计算问题解析
13、7,77,777,7777……,如果把前77个数相加,那么它们的和的末三位数是多少?_____。
A: 359B: 349C: 329D: 379
参考答案: A 本题解释:【答案】A。解析:把每一个数的末三位相加即可,也即7+77+777×75=58359。
14、在我国民间常用十二生肖进行纪年,十二生肖的排列顺序是鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪。2011年是兔年,那么2050年是_____。
A: 虎年B: 龙年C: 马年D: 狗年
参考答案: C 本题解释:正确答案是C考点周期问题解析(2050-2011)÷12=3······3,所以是兔年之后的第三个生肖,即马年。故正确答案为C。
15、有20名工人修筑一段公路,计划15天完成。动工3天后抽出5人去其他工地,其余人继续修路。如果每人工作效率不变,那么修完这段公路实际用_____
A: 19天B: 18天C: 17天D: 16天
参考答案: A 本题解释:【答案】A。解析:5人12天完成的工作量分配给15人需要5×12÷15=4天完成,所以修完这段公路实际用15+4=19天。
16、做一套衣服,上衣用布2.4米,裤子用布是上衣的2/5,做这套制服大约用布多少米?_____
A: 3.4B: 3.7C: 4.0D: 4.4
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析这套制服大约用布2.4×(1+2/5)=3.36米,故正确答案为A。
17、比-5大-7的数是_____。
A: -3B: 2C: -12D: -7
参考答案: C 本题解释: C [解析] -5+(-7)=-12。故本题选C。
18、小明前三次数学测验的平均分数是88分,要想平均分数达到90分以上,他第四次测验至少要达到_____
A: 98分B: 96分C: 94分D: 92分
参考答案: B 本题解释: 【解析】B。 分,该数值可以根据以上式子判定尾数为6,选择B。
分,该数值可以根据以上式子判定尾数为6,选择B。
19、某工程由小张、小王两人合作刚好可在规定的时间内完成。如果小张的工作效率提高20%,那么两人只需用规定时间的9/10就可完成工程;如果小王的工作效率降低25%,那么两人就需延迟2.5小时完成工程。问规定的时间是多长?_____
A: 20小时B: 24小时C: 26小时D: 30小时
参考答案: A 本题解释:正确答案是A考点工程问题解析由小张工作效率提高后两人完成工程的时间只用原来的9/10,可知提高效率前后的效率之比为9:10,也即两个人合作的效率提高了1/9。假定小张原来的工作效率为5,则现在提高了20%,也即效率增加了1,而增加的1占两人原合作效率的1/9,所以两人合作效率为9,于是可知小王的效率为4。而小王的工作效率降低25%,也即减少1,则两个人的合作效率变为8,前后效率之比为9:8,从而可知完成时间之比为8:9(这说明若规定时间看做8份的话,则现在要用的时间是9份,比原来多出1份),而题目给出延迟2.5小时,于是可知规定时间为2.5×8=20小时。故正确答案为A。
20、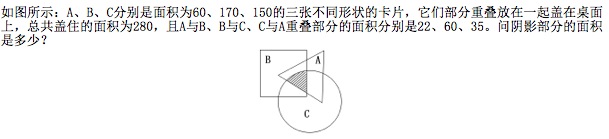 _____
_____
A: 15B: 16C: 17D: 18
参考答案: C 本题解释:正确答案是C考点容斥原理问题解析套用三集合容斥原理公式,60+170+150-22-60-35+X=280,根据尾数法知答案为C。三集合容斥原理公式:|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|B∩C|﹣|C∩A|+|A∩B∩C|。
21、不深不浅一口井,不长不短一根绳。单股下去多三尺,双股下去少三尺。问多深的井?多长的绳?_____
A: 井深六尺,绳长九尺B: 井深九尺,绳长一丈二C: 井深一丈七,绳长二丈D: 以上均不对
参考答案: B 本题解释:参考答案:B题目详解:设绳长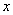 尺,井深
尺,井深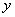 尺;可列方程:
尺;可列方程: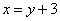 ,
,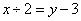 ,解得
,解得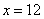 ,
,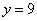 。所以,选B。考查点:数量关系>数学运算>盈亏问题
。所以,选B。考查点:数量关系>数学运算>盈亏问题
22、一学校的750名学生或上历史课,或上算术课,或两门课都上。如果有489名学生上历史课,606名学生上算术课,问有多少学生两门课都上?_____。
A: 117B: 144C: 261D: 345
参考答案: D 本题解释:参考答案 题目详解:解法一:设两门课都上的学生有x人。
题目详解:解法一:设两门课都上的学生有x人。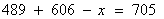
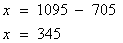 (原因:因为学数学的和学历史的人数和为1095人,但是全年级只有750人,这就说明有一部分同学是两科都学的,也就把两科都学的人算了两遍,所以只要减去年级总人数,剩下的就是两科都学的人数。)解法二:解设两门都上的人有
(原因:因为学数学的和学历史的人数和为1095人,但是全年级只有750人,这就说明有一部分同学是两科都学的,也就把两科都学的人算了两遍,所以只要减去年级总人数,剩下的就是两科都学的人数。)解法二:解设两门都上的人有 人,只学数学的人有
人,只学数学的人有 人,只学历史的人有
人,只学历史的人有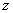 人。
人。 ①
①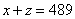 ②
②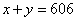 ③1-②得,
③1-②得,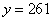 把
把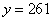 代入③中,得
代入③中,得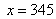 。所以,选D。解法三:直接用尾数法快解,秒杀题。
。所以,选D。解法三:直接用尾数法快解,秒杀题。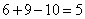 ,尾数为5的只有D。(该解析由用户“估计考不上”于2010-12-0213:04:48贡献,感谢感谢!)考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
,尾数为5的只有D。(该解析由用户“估计考不上”于2010-12-0213:04:48贡献,感谢感谢!)考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
23、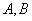 两地相距105千米,甲、乙两人骑自行车分别从两地同时相向而行,甲从
两地相距105千米,甲、乙两人骑自行车分别从两地同时相向而行,甲从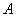 地出发,出发后经
地出发,出发后经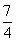 小时相遇,接着两人继续前进,在他们相遇3分钟后,一直以每小时40千米速度行驶的甲在途中与迎面而来的丙相遇,丙在与甲相遇后继续前进,在
小时相遇,接着两人继续前进,在他们相遇3分钟后,一直以每小时40千米速度行驶的甲在途中与迎面而来的丙相遇,丙在与甲相遇后继续前进,在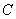 地赶上乙。如果开始时甲的速度比原速每小时慢20千米,而乙的速度比原速每小时快2千米。那么甲、乙就会在C地相遇,丙的骑车速度为_____千米/小时。
地赶上乙。如果开始时甲的速度比原速每小时慢20千米,而乙的速度比原速每小时快2千米。那么甲、乙就会在C地相遇,丙的骑车速度为_____千米/小时。
A: 20B: 24C: 23D: 23.2
参考答案: D 本题解释:参考答案 题目详解:两人的速度和是:
题目详解:两人的速度和是: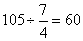 千米/小时,乙的速度是:60-40=20千米/小时。甲速度降低20千米/小时,乙速度提高2千米/小时后,两人的速度和:20+22=42千米/小时,相遇用时为
千米/小时,乙的速度是:60-40=20千米/小时。甲速度降低20千米/小时,乙速度提高2千米/小时后,两人的速度和:20+22=42千米/小时,相遇用时为 小时;甲行了
小时;甲行了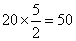 千米,因此
千米,因此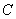 距离
距离 点50千米,第一次甲行了1小时48分钟后与丙相遇,此时距离
点50千米,第一次甲行了1小时48分钟后与丙相遇,此时距离 点72千米,第一次相遇乙走了36千米,距离
点72千米,第一次相遇乙走了36千米,距离 点69千米,丙与乙的追及距离是
点69千米,丙与乙的追及距离是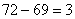 千米;最终丙在
千米;最终丙在 点追上乙,乙走了
点追上乙,乙走了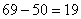 千米用时为
千米用时为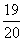 小时,则丙的速度是:
小时,则丙的速度是: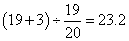 千米/小时。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
千米/小时。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
24、有8种颜色的小球,数量分别为2、3、4、5、6、7、8、9,将它们放进一个袋子里面,问拿到同颜色的球最多需要几次?_____
A: 6B: 7C: 8D: 9
参考答案: D 本题解释:【答案解析】解析:"抽屉原理"问题。先从最不利的情况入手,最不利的情况也就使次数最多的情况。即8种小球,每次取一个,且种类不相同(这就是最不利的情况)。然后任取一个,必有重复的,所以是最多取9个。
25、列车的速度为每小时50公里,汽船的速度每小时30公里,若列车开行2小时汽船开行3小时,则列车比汽船多行了_____公里。
A: 10B: 9C: 8D: 11
参考答案: A 本题解释:A本题相对来说简单化,只需求出列车与汽船路程之差就可以了;由题可得列车比汽船多行了50×2-30×3=10(公里),正确答案为A。
26、_____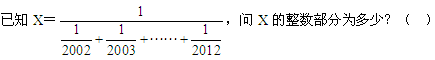
A: 182B: 186C: 194D: 196
参考答案: A 本题解释:正确答案是A考点不等式分析问题解析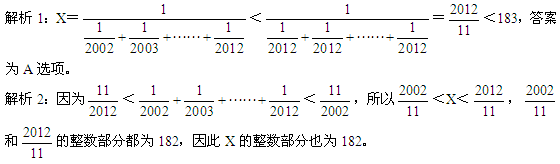 故正确答案为A。
故正确答案为A。
27、(2009•国考)甲、乙两人共有260本书,其中甲的书有13%是专业书,乙的书有12.5%是专业书,问甲有多少本非专业书?_____
A: 75B: 87C: 174D: 67
参考答案: B 本题解释:参考答案:B本题得分:题目详解:根据题意甲的专业书:甲的书有13%是专业书,即有甲的13/100是专业书;甲的书本数:由于书的本数为整数,则甲的书本数只能为100或200;乙的专业书:乙的书有12.5%是专业书,即有乙的1/8是专业书;乙的书本数:由于书的本数为整数,则乙的书本数必能被8整除;甲、乙两人共有260本书,甲的书本数为100或200,则乙的书的本数为160或60,其中只有160能被8整除,故乙的书本数为160,则甲有100本书,其非专业书本数为100×(1-13%)=87本。所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
28、甲、乙、丙三人买水果,甲买了3千克苹果和2千克梨,乙买了4千克苹果和3千克梨,丙买了3千克苹果和4千克梨。乙比甲多花7元,甲比丙少花5元。问甲、乙、丙共花了多少钱?_____。
A: 92.5元B: 112.5元C: 88.0元D: 67.5元
参考答案: D
29、一个三位数,各位上的数的和是15,百位上的数与个位上的数的差是5,如颠倒各位上的数的顺序,则所成的新数比原数的3倍少39。求这个三位数。_____
A: 196B: 348C: 267D: 429
参考答案: C 本题解释:【解析】C。代入法。首先排除A和D;根据所成的新数比原数的3倍少39,用每个选项的最后一个数乘以3再减去,所得的数只有C中有。
30、符号消费是指在消费过程中,消费者除消费产品本身以外,同时也消费这些产品所象征和代表的意义、心情、美感、档次、情调和气氛,即对这些符号所代表的“意义”或“内涵”的消费。根据上述定义,下列各项中体现了符号消费的是_____。
A: 大张和小伟结伴去背包旅行,小伟买了个专业登山包,大张随便背了个包就去了,结果被小伟嘲笑了一番B: 面点师小金每到一个地方,都会去当地知名的蛋糕店点上几份甜品,并且花上几个小时仔细品尝C: 某甜品店最近生意火爆,顾客都指明要该店新推出的一款特色饮品D: 老李退休后非常注重养生,买了一大堆的保健品
参考答案: A 本题解释:A。定义的关键词是“意义”和“内涵”。A项,小伟和大张的包都能够满足旅行的需要,但小伟嘲笑大张的包,说明他购买专业登山包,主要是消费它所代表的时尚、档次等“内涵”,并不是在于包本身,因此符合定义。B项,小金作为面点师,去仔细品尝知名蛋糕店的甜品,是为了改进、提高自己的手艺,而不单纯是为了消费,因而也就更谈不上是符号消费。C项,顾客购买新推出的特色产品,针对的是产品本身。D项,老李购买保健品是出于养生的需求,他消费的也是产品本身。
31、某房地产公司分别以80万人民币的相同价格出售两套房屋。一套房星以盈利20%的价格出售,另一套房屋以盈利30%的价格出售,那么该房地产公司从中获利约为_____。
A: 31.5万元B: 31.6万元C: 31.7万元D: 31.8万元
参考答案: D 本题解释:正确答案是D考点经济利润问题解析两套房屋一套盈利20%,一套盈利30%,因此每套房屋的成本分别为80÷(1+20%)万元和80÷(1+30%)万元,共获利80÷(1+20%)×20%+80÷(1+30%)×30%≈31.8万元,故正确答案为D。
32、市民广场中有两块草坪,其中一块草坪是正方形,面积为400平方米,另一块草坪是圆形,其直径比正方形边长长10%,圆形草坪的面积是多少平方米?_____
A: 410B: 400C: 390D: 380
参考答案: D 本题解释: 【解析】正方形的边长是20米,那么圆的半径是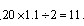 米,那么圆形草坪的面积是
米,那么圆形草坪的面积是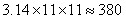 ,故选D。
,故选D。
33、(2009江苏,第74题)有一列士兵排成若干层的中空方阵,外层共有68人,中间一层共有44人,则该方阵士兵的总人数是_____。
A: 296人B: 308人C: 324人D: 348人
参考答案: B 本题解释:参考答案:B题目详解:依题意:最外层68人,中间一层44人,则最内层为 人(成等差数列);因此一共有:
人(成等差数列);因此一共有: (层);总人数为:
(层);总人数为: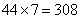 ;所以,选B。考查点:数量关系>数学运算>特殊情境问题>方阵问题>空心方阵问题
;所以,选B。考查点:数量关系>数学运算>特殊情境问题>方阵问题>空心方阵问题
34、甲、乙两数之和加上甲数是220,加上乙数是170,甲、乙两数之和是多少_____
A: 50B: 130C: 210D: 390
参考答案: B 本题解释: 【解析】B。由题意可知,2甲+乙=220,甲+2乙=170,两式相加,即3(甲+乙)=390,所以甲+乙=130。
35、科考队员在冰面上钻孔获取样本,测量不同空心之间的距离,获得的部分数据分别为1米、3米、6米、12米、24米、48米。问科考队员至少钻了多少个孔?_____
A: 4B: 5C: 6D: 7
参考答案: D 本题解释:正确答案是D考点几何问题解析所测距离组成一个数列1、3、6、12、24、48,易知该数列中任一项均大于其前面所有项之和,故这6条线段不可能组成封闭回路,即6条线段最少7个端点,至少钻7个孔。故正确答案为D。
36、有一条新修的道路,现在需要在该道路的两边植树,已知路长为5052米,如果每隔6米植一棵树,那么一共需要植多少棵树?_____
A: 1646B: 1648C: 1686D: 1628
参考答案: C 本题解释:正确答案是C考点计数模型问题解析这是一个双边线性植树模型,根据基本公式,棵树=2×(5052÷6+1)=2×(842+1)=1686(棵),故正确答案为C选项。注:双边线性植树,棵树=2×(路长÷间隔+1)。
37、大小两个数的和是50.886,较大数的小数点向左移动一位就等于较小的数,求较大的数是_____。
A: 46.25 B: 40.26 C: 46.15 D: 46.26
参考答案: D 本题解释:【解析】D。 四个选项的小数点后都是两位,两数之和为50.886,则两个数的尾数都为6,所以可以排除A、C两项。将B、D两项代入,只有D项符合。
38、甲、乙、丙、丁四人做纸花,已知甲、乙、丙三人平均每人做了37朵,乙、丙、丁三人平均每人做了39朵,已知丁做了41朵,问甲做了多少朵?_____
A: 35朵B: 36朵C: 37朵D: 38朵
参考答案: A 本题解释:正确答案是A考点平均数问题解析解析1:甲、乙、丙三人做的纸花的平均数比乙、丙、丁三人做的纸花的平均数小2,则甲比丁做的纸花少2×3=6朵,因此甲做了41-6=35朵,故正确答案为A。解析2:乙、丙、丁三人共做了39×3=117朵,乙、丙两人共做了117-41=76朵,甲、乙、丙三人共做了37×3=111朵,则甲做了111-76=35朵,故正确答案为A。
39、一圈金属线长30米,截取长度为A的金属线3根,长度为B的金属线5根,剩下的金属线如果再截取2根长度为B的金属线还差0.4米,如果再截取2根长度为A的金属线则还差2米.A等于几米?_____
A: 3.6B: 2.8C: 6.4D: 9.2
参考答案: A 本题解释:参考答案:A题目详解:列方程: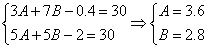 所以,选A。考查点:数量关系>数学运算>盈亏问题
所以,选A。考查点:数量关系>数学运算>盈亏问题
40、某人银行账户今年底余额减去1500元后,正好比去年底余额减少了25%,去年底余额比前年余额的120%少2000元,则此人银行账户今年底余额一定比前年底余额_____。
A: 多1000元B: 少1000元C: 多10%D: 少10%
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析设前年底余额为m元,则去年为(1.2m-2000)元,今年为[0.75×(1.2m-2000)+1500]元,化简得今年为0.9m元,即今年底余额比前年底减少10%,故正确答案为D。标签逆向考虑
41、某时刻时针和分针正好成90度的夹角,问至少经过多少时间,时针和分针又一次成90度夹角?_____
A: 30分钟B: 31.5分钟C: 32.2分钟D: 32.7分钟
参考答案: D 本题解释:正确答案是D考点钟表问题解析分针与时针的速度比为12:1,分针与时针成直角到再次成直角的过程中,分针比时针多走180度,即多转过30分钟的角度,因此分针实际走过的时间为30×(12/11)≈32.7分钟。故正确答案为D。标签画图分析
42、甲乙丙丁四个数的和为43,甲数的2倍加8,乙数的3倍,丙数的4倍,丁数的5倍减去4,都相等。这四个数各是多少?_____
A: 141289B: 161296C: 1110814D: 141298
参考答案: D 本题解释:正确答案是D考点计算问题解析解法1:设甲数为a,乙数为b,丙数为c,丁数为d,由题意有: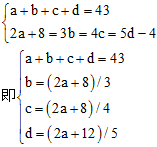 解得:a=14,b=12,c=9,d=8。故正确答案为D。解法2:由题意知四个数之和的尾数应为3,可排除B项;又因为甲的2倍加8等于丙的4倍,代入其余各项的值,可知A、C均错误。故正确答案为D。标签直接代入尾数法
解得:a=14,b=12,c=9,d=8。故正确答案为D。解法2:由题意知四个数之和的尾数应为3,可排除B项;又因为甲的2倍加8等于丙的4倍,代入其余各项的值,可知A、C均错误。故正确答案为D。标签直接代入尾数法
43、有一件工作,丙单独做需10小时完成;乙、丙合作需4小时完成。甲2小时完成的工作量,乙需要3小时才能完成。现在这件工作由丙独做,他从清晨5时开工,必须在中午12时完工。甲、乙二人应帮助丙工作多少时间才能使丙准时完成工作?_____
A: 4/5小时B: 1小时C: 4/3小时D: 2小时
参考答案: A 本题解释: 
44、某公司三名销售人员2011年的销售业绩如下:甲的销售额是乙和丙销售额的1.5倍,甲和乙的销售是丙的销售额的5倍,已知乙的销售额是56万元,问甲的销售额是_____。
A: 140万元B: 144万元C: 98万元D: 112万元
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析由题意,甲=1.5(乙+丙),甲+乙=5丙,将乙=56代入,可得甲=144,丙=40。故答案为B。秒杀技秒杀一:由甲的销售额是乙丙之和的1.5倍,而1.5中含有因子3,因此甲的销售额能被3整除,仅B符合。秒杀二:甲和乙的销售额之和是丙销售额的5倍,因此甲乙销售额之和能够被5整除,其尾数为0或5,在四个选项中仅B符合这一要求。
45、 _____
_____
A: AB: BC: CD: D
参考答案: A 本题解释:正确答案是A考点年龄问题解析y表示丙当年的年龄,10年前丙为y-10岁,10年前甲为(y-10)/2=y/2-5岁,5年前甲为y/2岁,5年前乙的年龄为(y/2)/3=y/6岁,则乙当前年龄为y/6+5岁。故正确答案为A。
46、有砖26块,兄弟二人争着去挑。弟弟抢在前面,刚摆好砖,哥哥赶到了。哥哥看弟弟挑的太多,就抢过一半。弟弟不肯,又从哥哥那儿抢走一半。哥哥不服,弟弟只好给哥哥5块,这时哥哥比弟弟多挑2块。问最初弟弟准备挑多少块?_____
A: 16 B: 15 C: 14 D: 13
参考答案: A 本题解释:A。【解析】先算出最后各挑几块:(和差问题)哥哥是(26+2)÷2=14,弟弟是26-14=12,然后来还原:1.哥哥还给弟弟5块:哥哥是14-5=9,弟弟是12+5=17;2.弟弟把抢走的一半还给哥哥:抢走了一半,那么剩下的就是另一半,所以哥哥就应该是9+9=18,弟弟是17-9=8;3.哥哥把抢走的一半还给弟弟:那么弟弟原来就是8+8=16块。
47、将一块三角形绿地沿一条直线分成两个区域,一块为三角形,一块为梯形,已知分出的三角形区域的面积为1.2亩,梯形区域的上、下底边分别为80米、240米,问分出的梯形区域的面积为多少亩?_____
A: 9.6B: 11.2C: 10.8D: 12.0
参考答案: A 本题解释:A。
48、袋子里装有红、蓝两色的小球各12个,先从袋子中拿出一个球,然后将它放回袋子中,混合后再从中拿出一个小球。那么两次抽中不同颜色的小球的几率有_____。
A: 20%B: 25%C: 50%D: 60%
参考答案: C 本题解释:【解析】因为两种颜色的小球数量相等,那么每次抽中其中一种颜色小球的概率均为50%。第一种情况:第一次抽中了红色小球,第二次抽中了蓝色小球,概率是50%×50%一25%;第二种情况:第一次抽中了蓝色小球,第二次抽中了红色小球,概率是50%×50%=25%。那么两次抽中不同颜色的小球的整体概率等于两种情况下的概率之和,即25%+25%=50%,答案为C。
49、某S为自然数,被10除余数是9,被9除余数是8,被8除余数是7,已知100<S<1000,请问这样的数有几个?_____
A: 5 B: 4 C: 3 D: 2
参考答案: D 本题解释:D。【解析】被N除余数是N-1,所以这个数字就是几个N的公倍数-1。10,9,8的公倍数为360n(n为自然数),因为100<S<1000,所以有两个数符合条件。
50、如图所示,在3×3方格内填入恰当的数后,可使每行、每列以及两条对角线上的三数的和都相等。问方格内的x的值是多少?_____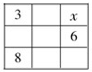
A: 2B: 9C: 14D: 27
参考答案: A 本题解释:正确答案是A考点趣味数学问题解析假定中间数字为a,则a+6=8+3,则a=5。而3+a=x+6,解得x=2,故正确答案为A。
51、某学校组织学生春游,往返目的地时租用可乘坐10名乘客的面包车,每辆面包车往返的租金为250元。此外,每名学生的景点门票和午餐费用为40元,如果求尽可能少租车,则以下哪个图形最能反映平均每名学生的春游费用支出与参加人数之间的关系:_____
A: AB: BC: CD: D
参考答案: B 本题解释:正确答案是B,解析方法一:分段表示平均费用和总人数之间的关系,设人数为 。当人数
。当人数 在
在 之间时,总的费用为
之间时,总的费用为 ,平均费用为
,平均费用为 ,这是一个双曲线;当人数
,这是一个双曲线;当人数 在
在 之间时,总费用变成
之间时,总费用变成 ,平均费用为
,平均费用为 ,左节点明显大于上一个区间的右节点的,之后的区间类似,故答案选择B选项。方法二:结合图形,代入人数等于1、10、11大致判断。故正确答案为B。
,左节点明显大于上一个区间的右节点的,之后的区间类似,故答案选择B选项。方法二:结合图形,代入人数等于1、10、11大致判断。故正确答案为B。
52、减数、被减数与差三者之和除以被减数,商是多少_____
A: 0B: 1C: 2D: 减数与差之和
参考答案: C 本题解释: 【解析】C。减数+被减数+差=2被减数,所以商为2。
53、甲单位义务植树一公里,乙单位紧靠甲单位又植树一公里,如果按10米植一棵树的话,两单位共植树多少棵?_____
A: 199B: 200C: 201D: 202
参考答案: C 本题解释:参考答案:C题目详解:此题要求两单位的植树总数,则分甲单位植树的棵数和乙单位植树的棵数。甲单位在一公里内植树,则两端均可植一棵树,带入两端均植树问题的公式:棵数=总长÷间距+1=1000÷10+1=101棵树;乙单位紧靠着甲单位植树,则有一端不需要植树,带入只有一端植树问题的公式:棵数=总长÷间距=1000÷10=100棵树。因此,甲、乙共植树:101+100=201棵。所以,选C。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树
54、将棱长为1的正方体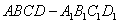 ,切去一角
,切去一角 后,剩下几何体的表面积是_____。
后,剩下几何体的表面积是_____。
A: 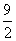 B: 5C:
B: 5C: 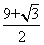 D:
D: 
参考答案: C 本题解释:参考答案:C题目详解:如右图所示,可知:原正方体表面积: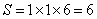 ;减少的表面积为:
;减少的表面积为: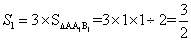 ;增加的表面积为:
;增加的表面积为: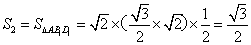 ;故剩下面积为:
;故剩下面积为: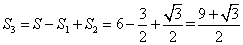 。所以,选C。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选C。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
55、某公司招聘员工,按规定每人至多可投考两个职位,结果共42人报名,甲、乙、丙三个职位报名人数分别是22人、16人、25人,其中同时报甲、乙职位的人数为8人,同时报甲、丙职位的人数为6人,那么同时报乙、丙职位的人数为_____。
A: 7人B: 8人C: 5人D: 6人
参考答案: A 本题解释:正确答案是A考点容斥原理问题解析三集合容斥原理公式,42=22+16+25-8-6-x+0,根据尾数法可知x=7。故答案为A。标签三集合容斥原理公式尾数法
56、有一种长方形小纸板,长为19毫米,宽为11毫米。现在用同样大小的这种小纸板拼合成一个正方形,问最少要几块这样的小纸板拼合成一个正方形,问最少要几块这样的小纸板?_____
A: 157块B: 172块C: 209块D: 以上都不对
参考答案: C 本题解释:参考答案:C题目详解:本题可转化为:求19与11的最小公倍数,即为:19×11=209;则组成正方形的边长为209,从而可得组成正方形的小纸板数为: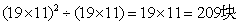 ;所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>两个数的最大公约数和最小公倍数
;所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>两个数的最大公约数和最小公倍数
57、把几百个苹果平均分成若干份,每份9个余8个,每份8个余7个,每份7个余6个。这堆苹果共有多少个?_____
A: 111B: 143C: 251D: 503
参考答案: D 本题解释:参考答案:D题目详解:此题为剩余定理中差同的情况,根据"差同减差,最小公倍数做周期"可知:即苹果数加上一个,就是7、8和9的公倍数;而7、8和9的最小公倍数是504,正好在几百的范围内:因此这堆苹果有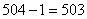 个;所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>差同
个;所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>差同
58、一条街上,一个骑车人和一个步行人相向而行,骑车人的速度是步行人的3倍,每个隔10分钟有一辆公交车超过一个行人。每个隔20分钟有一辆公交车超过一个骑车人,如果公交车从始发站每隔相同的时间发一辆车,那么间隔几分钟发一辆公交车?_____
A: 10B: 8C: 6D: 4
参考答案: B 本题解释:B。【解析】设车速V车,人速V人,自行车速3V人,则(V车-V人)×10=20×(V车-3V人),V车=5V人,即车走人4倍位移追上人故T=4×V人×10/5V人=8。
59、在一条公路两旁有四家工厂,工厂的职工人数如右图所示,现在要在这段路线上设立一个公共汽车站。问这个车站设在什么地方,可以使几家工厂的职工乘车方便?_____
A: 甲厂B: 乙厂C: 丙厂D: 丁厂
参考答案: C 本题解释:C【解析】四个工厂的职工人数总和的一半是:(1000+700+800+500)÷2=1500(人)。甲厂500人,丁厂1000人,它们都小于四厂总人数的一半。根据“小靠大”的原则,甲厂附近和丁厂附近都不是车站的最佳位置。甲厂与丁厂要分别向乙厂和丙厂靠,这样丙厂就相当于1000+700=1700(人),乙厂就相当于500+800=1300(人)。再由“小靠大”的原则,1700>1300,所以乙厂应向丙厂靠,即车站设在丙厂附近为最佳。故本题正确答案为C。
60、一个圆形牧场面积为3平方公里,牧民骑马以每小时18公里的速度围着牧场外沿巡视一圈,约需多少分钟?_____
A: 12B: 18C: 20D: 24
参考答案: C 本题解释:正确答案是C考点几何问题解析
61、从12时到13时,钟的时针与分针可成直角的机会有_____。
A: 1次B: 2次C: 3次D: 4次
参考答案: B 本题解释:【答案解析】一个小时内成直角只有两次,选B。
62、有10粒糖,如果每天至少吃一粒(多不限),吃完为止,求有多少种不同吃法?_____
A: 144B: 217C: 512D: 640
参考答案: C 本题解释:参考答案:C题目详解:应用插板法:将10粒糖并列一排放置,中间形成9个空位,在这9个空位中任意插入0~9个隔板,(即表示10粒糖在1到10天吃完);故共有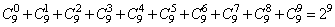 ;即有512种吃法。所以,选C。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
;即有512种吃法。所以,选C。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
63、某单位有60名运动员参加运动会开幕式,他们着装白色或黑色上衣,黑色或蓝色裤子。其中有12人穿白上衣蓝裤子,有34人穿黑裤子,29人穿黑上衣,那么穿黑上衣黑裤子的有多少人? _____
A: 12B: 14C: 15D: 19
参考答案: C 本题解释:C。【解析】有34人穿黑裤子,则有60-34=26个人穿蓝色裤子,26-12=14个人穿黑衣蓝裤,则有29-14=15个人穿黑衣黑裤
64、2006×20072007-2007×20062006的值为_____。
A: ﹣10C: 100D: 1000
参考答案: B 本题解释:正确答案是B考点多位数问题解析原式=2006×(20070000+2007)-2007×(20060000+2006)=2006×2007×10000+2006×2007-2007×2006×10000-2007×2006=0,故正确答案为B。
65、取甲种硫酸300克和乙种硫酸250克,再加水200克,可混合成浓度为50%的硫酸;而取甲种硫酸200克和乙种硫酸150克,再加上纯硫酸200克,可混合成浓度为80%的硫酸。那么,甲、乙两种硫酸的浓度各是多少?_____
A: 75%,60%B: 68%,63%C: 71%,73%D: 59%,65%
参考答案: A 本题解释:【答案】A。解析:
66、已知29832983…298302能被18整除,那么n的最小值是_____。
A: 4B: 5C: 6D: 7
参考答案: A 本题解释:【解析】18=2×9,这个多位数的个位上是2,满足被2整除,因此,只需考虑个位数字之和能否被9整除的问题。(2+9+8+3)×n+0+2=22n+2是9的倍数,22×4+2=90=9×10,那么n的最小值为4。
67、商场的自动扶梯以匀速由下往上行驶,两个孩子在行驶的扶梯上上下走动,女孩由下往上走,男孩由上往下走,结果女孩走了40级到达楼上,男孩走了80级到达楼下。如果男孩单位时间内走的扶梯级数是女孩的2倍。则当该扶梯静止时,可看到的扶梯梯级有_____。
A: 8时12分B: 8时15分C: 8时24分D: 8时30分
参考答案: C 本题解释:正确答案是B考点行程问题解析
68、甲、乙两人共储蓄1000元,甲取出240元,乙又存入80元,这时甲的储蓄正好是乙的3倍,原来甲比乙多储蓄多少元?_____
A: 620元B: 740元C: 700元D: 660元
参考答案: B 本题解释:正确答案:B解析:假设甲储蓄的钱为X,则乙为1000-X,那么X-240=3(1000-X+80),X=870,则乙为1000-870=130。甲比乙多870-130=740元。故答案为B。
69、有两个班的小学生要到少年宫参加活动,但只有一辆车接送。第一班的学生坐车从学校出发的同时,第二班学生开始步行。车到途中某处,让第一班学生下车步行,车立刻返回接第二班学生上车并直接开往少年宫,学生步行速度为每小时4公里,载学生时车速每小时40公里,空车每小时50公里,那么,要使两班学生同时到达少年宫,第一班学生步行了全程的几分之几?(学生上下车时间不计)_____。
A: 1/7B: 1/6C: 3/4D: 2/5
参考答案: A 本题解释:正确答案是A考点行程问题解析为了使两班同时到达,必须满足一个条件,即两班行走的距离相等,坐车的距离也相等。设二班步行的距离为x,一班坐车的距离为y,则一班行走的距离也为x,二班的坐车距离为y。由线段图可知:二班步行时间=(一班坐车时间+空车跑回接二班的时间),所以得x/4=y/40+(y-x)/50,解得x/y=1/6,所以x占全程的1/7,故正确答案为A。
70、7个同学排成两排照相,前排3人,后排4人,共有_____种站法。
A: 1680B: 2400C: 2520D: 5040
参考答案: D 本题解释:【解析】相当于把7个元素放在预先指定好的7个不同位置上,因此,是7个同学的全排列,共有P77=5040种站法。
71、某市为合理用电,鼓励各用户安装峰谷电表,市原电价每度0.53元,改新表后,每晚10点至次日早8点为低谷,每度收0.28元,其余时间为高峰期,每度0.56元,为改装新电表每个用户须收取100元改装费,假定某用户每月用200度电,两个不同时段用电量各为100度,那么改装电表12个月后,该用户可节约_____元。
A: 161B: 162C: 163D: 164
参考答案: D 本题解释:正确答案是D考点经济利润问题解析电表改装之前该用户每年的用电费用为200×0.53×12=1272元;改装电表之后,该用户这一年的用电费用加上改装费用共(0.28×100+0.56×100)×12+100=1108元,该用户改装电表前后可节约1272-1108=164元。故正确答案为D。
72、用直线切割一个有限平面,后一条直线与此前每条直线都要产生新的交点,第1条直线将平面分成2块,第2条直线将平面分成4块。第3条直线将平面分成7块,按此规律将平面分为22块需_____。
A: 7条直线B: 8条直线C: 9条直线D: 6条直线
参考答案: D 本题解释:正确答案是D考点几何问题解析根据题意可知,设n为直线,S为分成的平面数,n=1时,S=2;n=2时,S=4;n=3时,S=7;n=4时,S=11;n=5时,S=16;n=6时,S=22。所以6条线可将平面分成22部分。故答案为D。
73、从装满1000克浓度为50%的酒精瓶中倒出200克酒精,再倒入蒸馏水将瓶加满。这样反复三次后,瓶中的酒精浓度是多少?(X)
A: 22.5%B: 24.4%C: 25.6%D: 27.5%
参考答案: 本题解释:正确答案是C考点浓度问题解析解析1:先道出溶液再倒入清水,套用公式,浓度= ,所以答案为C。
,所以答案为C。 解析2:由题意:每次操作后,酒精浓度变为原来的(1000-200)÷1000=0.8,故反复三次后浓度变为50%×0.8×0.8×0.8=25.6%。标签公式应用
解析2:由题意:每次操作后,酒精浓度变为原来的(1000-200)÷1000=0.8,故反复三次后浓度变为50%×0.8×0.8×0.8=25.6%。标签公式应用
74、小明和小红积极参加红领巾储蓄活动,把零用钱存入银行。小明存入银行的钱比小红少20元。如果两人都从银行取出12元买学习用品,那么小红剩下的钱是小明的3倍。问两人原来共存入银行多少元?_____
A: 44B: 64C: 75D: 86
参考答案: B 本题解释: B【解析】设小明存入银行x元,则小红存入银行(x+20)元。由题意可得:(x-12)×3=(x+20)-12,故x=22。所以两人原来共存入银行22+(22+20)=64(元)。
75、小王步行的速度比跑步慢50%,跑步的速度比骑车慢50%。如果他骑车从A城去B城,再步行返回A城共需要2小时。问小王跑步从A城到B城需要多少分钟?_____
A: 45B: 48C: 56D: 60
参考答案: B 本题解释:正确答案是B考点行程问题解析 故正确答案为B。标签赋值思想公式应用
故正确答案为B。标签赋值思想公式应用
76、有3个企业共订阅300份《经济周刊》杂志,每个企业至少订99份,最多订101份,问一共有多少种不同的订法? _____
A: 6B: 7C: 8D: 9
参考答案: B 本题解释:B。【解析】份数的选择有99,100,101或100,100,100,则第一种选择有A33=6种订法,6+1=7
77、
78、某家店准备打折出售一批滞销的电脑,经核算,如果按正价打九折销售,每台还可盈利305元,如果打八折,就要亏损175元。那么这种电脑的进货价是_____元。
A: 4800B: 4625C: 4015D: 3940
参考答案: C 本题解释:这种电脑打九折和打八折的差价是305+175=480(元),那么正价为480÷(90%-80%)=4800(元),进货价为4800×90%-305=4015(元)。故本题答案为C。
79、一个容器内有若干克盐水。往容器内加入一些水,溶液的浓度变为3%,再加入同样多的水,溶液的浓度为2%,问第三次再加入同样多的水后,溶液的浓度是多少?_____
A: 1.8%B: 1.5%C: 1%D: 0.5%
参考答案: B 本题解释:正确答案是B考点浓度问题解析设盐的质量为3克,则浓度为3%的溶液的质量为3÷3%=100克,浓度为2%的溶液的质量为3÷2%=150克,加入的水为150-100=50克,再加50克水,溶液的浓度变为3÷(150+50)=1.5%,故正确答案为B。
80、公司某部门80%的员工有本科以上学历,70%有销售经验。60%在生产一线工作过,该部门既有本科以上学历,又有销售经历,还在生产一线工作过的员工至少占员工_____。
A: 20%B: 15%C: 10%D: 5%
参考答案: C 本题解释:正确答案是C考点容斥原理问题解析根据题意,有20%的员工没有本科以上学历,30%的员工没有销售经验,40%的员工没在生产一线工作过,则要使既有本科以上学历,又有销售经历,还在生产一线工作过的员工最少,需使不同时满足这三个条件的员工数最多,即为:20%+30%+40%=90%,则同时满足这三个条件的员工至少占总员工的10%,故正确答案为C。
81、某城市9月平均气温为28.5度,如当月最热日和最冷日的平均气温相差不超过10度,则该月平均气温在30度及以上的日子最多有多少天?_____
A: 24B: 25C: 26D: 27
参考答案: B 本题解释:正确答案是B考点多位数问题解析要使30度以上的天数尽可能多,在气温总和一定的情况下,则必然是其他天的温度尽可能低,而由最热日与最冷日的平均气温相差不超过10度,据此构造极端情况,最热天全部为30度,其余天为最冷天,温度为20度,设平均气温为30度的天数为x,则可得30x+20(30-x)=30×28.5,解得x=25.5,因此最多有25天。故正确答案为B。
82、某市一条大街长7200米,从起点到终点共设有9个车站,那么每个车站之间的平均距离是_____。
A: 780米B: 800米C: 850米D: 900米
参考答案: D 本题解释:正确答案是D考点计数模型问题解析该问题为计数模型中的植树问题。车站间的平均距离为7200÷(9-1)=900。故正确答案为D。
83、有一个啤酒桶,每天都会漏等量的酒。现在让8个人喝这个酒桶里的酒,4天可以喝完。如果让5个人来喝酒,则6天可以喝完。那么每天的漏酒量为原有酒的_____。
A:  B:
B: 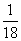 C:
C: 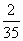 D:
D: 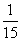
参考答案: A 本题解释:参考答案:A题目详解:依题意:设原有酒量为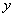 ;每天漏酒量为
;每天漏酒量为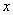 ,由于是减少量,“-”变为“+”;代入公式:
,由于是减少量,“-”变为“+”;代入公式: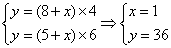 即:
即: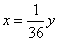 ;所以,选A。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
;所以,选A。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
84、18名游泳运动员,有8名参加仰泳,有10名参加蛙泳,有12名参加自由泳,有4名既参加仰泳又参加蛙泳,有6名既参加蛙泳又参加自由泳,有5名既参加仰泳又参加自由泳,有2名这3个项目都参加。这18名游泳运动员中,只参加1个项目的有多少名?_____
A: 5B: 6C: 7D: 4
参考答案: B 本题解释: 【解析】B。利用文氏图可以迅速准确地求得答案。注意本题目的陷阱,18名运动员并不是都参加了项目。 由图可知;只参加一个项目的有l+2=3=6名。
由图可知;只参加一个项目的有l+2=3=6名。
85、正四面体的棱长增长10%,则表面积增加_____
A: 21%B: 15%C: 44%D: 40%
参考答案: A 本题解释:参考答案:A题目详解:根据题意,可知:正四面体就是四个相等的正三角形。设原棱长a为1,则:原表面积为: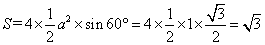 ;现表面积为:
;现表面积为: ;所以
;所以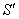 比S增加了:
比S增加了: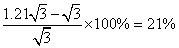 。所以,选A。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选A。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
86、某公安行动组有成员若干名,如果有一名女同志在外执勤,剩下组员中1/4是女性;如果有3名男同志在外执勤,剩下组员中有2/5是女性。如果行动组要派出男女各2名组员在外执勤,那么执勤人员的组成方式有_____种。
A: 168B: 216C: 286D: 356
参考答案: B 本题解释:正确答案是B考点排列组合问题解析
87、某人将一套房屋以购入价的3倍在房产中介处放盘。他告诉中介,一周内签约的买家其成交价能比放盘价再便宜5万元,并愿意支付成交价3%的中介费基础上,再多支付1万元给中介。若该房屋在一周内以100万元的价格成交,那么,此人在这套房屋上盈利_____万
A: 66B: 65C: 61D: 58
参考答案: C 本题解释:【答案】C。解析:成交价100,则据题意放盘价是100+5=105,可知购入价是105÷3=35,中介费是100X3%+1=3+1=4.可知盈利100-35-4=61。因此,本题答案选择C项。
88、某天,林伯的水果摊三种水果的价格分别为:苹果6元/斤,芒果5元/斤,香蕉3/斤。当天,苹果与芒果的销售量之比为4:3,芒果与香蕉的销售量之比为2:11,卖香蕉比卖苹果多收入102元,林伯这天共销售三种水果_____斤。
A: 75B: 94C: 141D: 165
参考答案: B 本题解释:正确答案是B考点经济利润问题解析将两个比例合并:苹果与芒果的销售量之比为8:6,芒果与香蕉的销售量之比为6:33。故苹果、芒果、香蕉的销售量之比为8:6:33。故设三者的销售量分别为8x、6x、33x,从而有3×33x-6×8x=102,解得x=2。故共销售水果(8+6+33)×2=94斤。故正确答案为B。
89、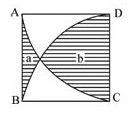
A: 13.75cmB: 14.25cmC: 14.75cmD: 15.25cm
参考答案: B 本题解释:正确答案是B考点几何问题解析
90、3×999+8×99+4×9+8+7的值是_____。
A: 3840B: 3855C: 3866D: 3877
参考答案: A 本题解释:正确答案是A考点计算问题解析由于各选项尾数均不相同,故可用尾数法确定正确答案。原式各项尾数之和为7+2+6+8+7,其计算值尾数为0,故原式计算值尾数亦为0。各选项中仅3840符合,于是正确答案为A。标签尾数法
91、某年级有四个班级,不算一班有210人,不算二班有199人,不算三班有196人,不算四班有205人,问:这个年级共有_____人?
A: 240B: 270C: 320D: 3 60
参考答案: B 本题解释:B【解析】设一、二、三、四班的人数分别为a,b,c,d人。不算一班的人数是210人,即b+c+d=210;不算二班的人数是199人,即a+c+d=199;不算三班的人数是196人,即a+b+d=196;不算四班的人数为205人,即a+b+c=205;四个式子相加:3(a+k+c+d)=810。a+b+c+d=270,即这个年级共有270人,故应选B。
92、一小型货车站最大容量为50辆车,现有30辆车,已知每小时驶出8辆,驶入10辆,则多少小时车站容量饱和?_____
A: 8B: 10C: 12D: 14
参考答案: B 本题解释:B[解析]每小时驶出8辆,驶入10辆的结果就是每小时车站增加两辆车,以此类推,10个小时车站增加20辆,容量饱和。
93、某公司中午订餐,周一有27人订餐,周二有39人订餐,周三有43人订餐,周四有41人订餐,周五有39人订餐。如果在这五天至少有一天订餐的人有39人,那么五天都订餐的最多有多少人?_____
A: 27B: 26C: 25D: 24
参考答案: A 本题解释:参考答案:A题目详解:依题意:将39人分为仅订餐一次和五天都订餐的;那么五天都订餐的最多有: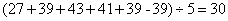 人;而周一只有27人订餐;因此最多只有27人五天都订餐。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
人;而周一只有27人订餐;因此最多只有27人五天都订餐。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
94、某人在公共汽车上发现一个小偷向相反方向步行,10秒钟后他下车去追小偷,如果他的速度比小偷快一倍,比汽车慢4/5,则此人追上小偷需要_____。
A: 20秒B: 50秒C: 95秒D: 110秒
参考答案: D 本题解释:正确答案是D考点行程问题解析根据题中三者速度的比例关系,设此人、小偷和汽车的速度分别为2、1、10,10秒钟后此人下车时,与小偷的距离为10×(10+1)=110,与小偷的速度差为1,因此所需时间为110秒,故正确答案为D。
95、小孙的口袋里有四颗糖,一颗巧克力味的,一颗果味的,两颗牛奶味的。小孙任意从口袋里取出两颗糖,他看了看后说,其中一颗是牛奶味的。问小孙取出的另一颗糖也是牛奶味的可能性(概率)是多少?_____
A: 1/3B: 1/4C: 1/5D: 1/6
参考答案: C 本题解释:正确答案是C考点概率问题解析两颗都是牛奶味的糖只有一种情况,而其中至少一颗是牛奶味的糖共有5种情况:(牛奶味1、苹果味),(牛奶味1、巧克力味),(牛奶味2、苹果味),(牛奶味2、巧克力味),(牛奶味1、牛奶味2),特别注意这里没有顺序要求,是组合。因此概率为1/5,故正确答案为C。标签分类分步
96、某国家对居民收入实行下列税率方案:每人每月不超过3000美元的部分按照1%税率征收,超过3000美元不超过6000美元的部分按照x%税率征收,超过6000美元的部分按y%税率征收(X、Y为整数)。假设该国某居民月收入为6500美元,支付了l20美元所得税,则Y为多少?_____
A: 6B: 3C: 5D: 4
参考答案: A 本题解释:A。由题意可得方程:3000×1%+3000×X%+500×Y%=120,化简得6X+Y=18,因为X、Y均为整数,代入各选项,只有A项中Y=6符合题意。
97、两列火车同向而行,甲车每小时行54千米,乙车每小时行72千米。甲车上一乘客发现:从乙车车头经过他的车窗时开始到乙车车尾经过他的车窗共用了70秒,乙车的车长是_____米。
A: 700B: 400C: 300D: 350
参考答案: D 本题解释:正确答案是D考点行程问题解析甲车的速度是54千米/小时=15米/秒,乙车的速度为72千米/小时=20米/秒。该运动过程实际是乙车车尾与该乘客的追及过程,追及距离为乙车的车长。因此乙车的车长为(20-15)×70=350米,故正确答案为D。公式:追及问题。追及距离=(大速度-小速度)×追及时间。标签公式应用
98、6个空瓶可以换一瓶汽水,某班同学喝了157瓶汽水,其中有一些是用喝剩下来的空瓶换的,那么他们至少要买多少瓶汽水?_____
A: 131B: 130C: 128D: 127
参考答案: A 本题解释:正确答案是A考点计数模型问题解析典型的空瓶换水问题,根据等价公式,6个空瓶可换一瓶水→6空瓶=1瓶水+1空瓶→5空瓶=1瓶水。设买了x瓶汽水,有x+x/5=157,解得x=130.8,取整得x=131,即至少要买131瓶水,故正确答案为A。等价公式:若M个空瓶换一瓶水,相当于M-1个空瓶可以喝到1瓶水。
99、四人进行篮球传接球练习,要求每人接球后再传给别人。开始由甲发球,并作为第一次传球,若第五次传球后,球又回到甲手中,则共有传球方式_____。
A: 60种B: 65种C: 70种D: 75种
参考答案: A 本题解释:[解析]正确答案为A。细分一下传球路径,第一次接球的人只能是非甲,第二第三次接球的人可能是甲或非甲,第四次接球的人只能是非甲,第五次接球的人一定是甲,每次传球后接到球的人可分析如下:第一次第二次第三次第四次第五次第一种情况:非甲甲非甲非甲甲第二种情况:非甲非甲甲非甲甲第三种情况:非甲非甲非甲非甲甲按排列组合,第一种情况的传球方式有3×1×3×2×1=18,第二种有3×2×1×3×1=18,第三种情况有3×2×2×2×l=24,相加共有60种,故选A。
100、由1、2、3组成没有重复数字的所有三位数之和是多少?_____
A: 1222B: 1232C: 1322D: 1332
参考答案: D 本题解释:正确答案是D考点计算问题解析解析1:没有重复的数字有6个:123、132、213、231、321、312,和为123+132+213+231+312+321=1332。故正确答案为D。解析2:没有重复的数字有6个,在每一个数位,1、2、3分别出现2次,所以数字之和为(1+2+3)×2×100+(1+2+3)×2×10+(1+2+3)×2×1=1332,故正确答案为D。