1、施工队要在一东西长600米的礼堂顶部沿东西方向安装一排吊灯，根据施工要求，必须在距西墙375米处安装一盏，并且各吊灯在东西墙之间均匀排列(墙角不能装灯)。该施工队至少需要安装多少盏吊灯？_____
A: 6 B: 7 C: 8 D: 9
参考答案: B 本题解释:【答案】B。解析：375与600的最大公约数为75,600÷75=8，两端不安装吊灯，则中间需要安8-1=7盏灯。

2、如果两个四位数的差等于8921，那么就说这两个四位数组成一个数对，问这样的数对共有多少个?_____
A: 80B: 79C: 83D: 81
参考答案: B 本题解释:【解析】从两个极端来考虑这个问题：最大为9999-1078=8921，最小为9921-1000=8921，所以共有9999-9921+1=79个，或1078-1000+1=79个。故应选择B。

3、某大型项目考察团队的所有员工年龄都在26～35岁之间，问：改考察团队至少有多少人才能保证在同一年出生的有5人？_____
A: 41B: 49C: 50D: 51
参考答案: A 本题解释:【答案】A。解析：最不利情况就是每年出生的人都有4个人，做题方法：最不利的情况数+1=4×10+1=41

4、小王和小李6小时共打印了900页文件，小王比小李快50%。请问小王每小时打印多少页文件?_____
A: 60B: 70C: 80D: 90
参考答案: D 本题解释:答案：D【解析】设小王每小时打印X页，因为小王比小李快50%，则小李每小时打印为X（1-50%）页，则根据题意可列：6X（1-50%）+6X=900，则X=90。

5、某服装厂要生产一批某种型号的学生服，已知每3米长的某种面料可做上衣2件。或做裤子3条，计划用300米长的这种布料生产学生服，应用多少米布料产生上衣，才能恰好配套?_____
A: 120B: 150C: 180D: 210
参考答案: C 本题解释:答案：C【解析】3米长可做上衣2件，或裤子3条，则300米布料可做上衣200件，或裤子300条，即如需成套，则上衣和裤子的数量必须同样多，那么上衣所用布料当为3/5，即180米，裤子为120米，共可做120套服装。所以答案为选项C。

6、某餐厅开展“每消费50元送饮料一瓶”的活动，某办公室的职员一起去该餐厅吃饭，每人花费18元，餐厅赠送了7瓶饮料。问去吃饭的人数可能是多少?_____
A: 17B: 19C: 21D: 23
参考答案: C 本题解释:C。送7瓶饮料说明总消费金额大于350小于400，代人选项发现只有21人时是21×18=378元符合条件。

7、一项工程如果交给甲乙两队共同施工，8天能完成；如果交给甲丙两队共同施工，10天能完成；如果交给甲丁两队共同施工，15天能完成；如果交给乙丙丁三队共同施工，6天就可以完成。如果甲队独立施工，需要多少天完成？_____
A: 16 B: 20C: 24D: 28
参考答案: C 本题解释:【解析】C。本题为工程问题，设工作总量为120，则甲乙工作效率和为15、甲丙工作效率和为12、甲丁工作效率和为8、乙丙丁效率和为20，可得甲的效率为（15+12+8-20）÷3=5，则甲单独完成需要120÷5=24天。所以选择C选项。

8、一只猎豹锁定了距离自己200米远的一只羚羊，以108千米/小时的速度发起进攻，2秒钟后，羚羊意识到危险，以72千米/小时的速度快速逃命。问猎豹捕捉到羚羊时，羚羊跑了多少路程？_____
A: 520米 B: 360米 C: 280米 D: 240米
参考答案: C 本题解释:【答案】C。解析：108千米/小时=30米/秒，72千米/小时=20米/秒，开始猎豹距离羚羊200米，羚羊意识到危险的时候，猎豹距离羚羊200米-30米/秒×2秒=140米。根据追击问题计算公式：速度差×追击时间=路程差，即（30-20）t=140，t=14秒，即猎豹捕捉到羚羊时，羚羊跑了14秒，路程为20×14=280米。

9、有一个长方体容器，长40厘米，宽30厘米，高10厘米，里面的水深6厘米(最大面为底面)。如果把这个容器盖紧，再竖起来(最小面为底面)，则里面的水深是多少厘米_____
A: 15厘米 B: 18厘米 C: 24厘米 D: 30厘米
参考答案: C 本题解释:【解析】C。盖紧后竖起前水的底面积为40×30平方厘米，深为6厘米，则体积为40×30×6立方厘米。盖紧后竖起水的体积不变，底面积变成了30×10平方厘米，此时水深应为。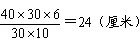

10、甲乙丙的速度之比为3：4：5，经过相同的一段路，三人所用时间之比：_____
A: 3：4：5　 B: 5：4：3 C: 20：15：12 D: 12：8：5
参考答案: C 本题解释:C【解析】根据公式“时间=路程÷速度”可知，经过相同的路程，甲、乙、丙的时间比为1/3:1/4:1/5=20:15:12。

11、科学家对平海岛屿进行调查，他们先捕获30只麻雀进行标记，后放飞，再捕捉50只，其中有标记的有10只，则这一岛屿上的麻雀大约有多少只?_____
A: 150只B: 300只C: 500只D: 1 500只
参考答案: A

12、200除500，商2余100，如果被除数和除数都扩大3倍，则余数是_____。
A: 100B: 200C: 300D: 100000
参考答案: C 本题解释:【解析】商不变，余数跟着扩大3倍，所以是300，选C。

13、152个球，放入若干个同样的箱子中，一个箱子最少放10个，最多放20个，且各个箱子的球数均不相同，问有多少种放法?(不计箱子的排列，即两种放法，经过箱子的重新排列后，是一样的，就算一种放法)_____
A: 1B: 7C: 12D: 24
参考答案: A 本题解释:A【解析】 设箱子个数为m，因为每只箱子的球数均不相同，最少放10个，最多放20个，所以m≤20-10+1=11。如果m=11，那么球的总数≥10×11+（0+1+2+…+10）=110+55>152，所以m≤10。如果m≤9，那么球的总数≤10×9+（10+9+8+…+2）=90+54=144<152，所以m=10在m=10时，10×10+（10+9+…+1）=155=152+3，所以一个箱子放10个球，其余箱子分别放11，12，14，15，16，17，18，19，20个球，总数恰好为152，而且符合要求的放法也只有这一种。故本题正确答案为A。

14、一个三位数除以43，商是a，余数是b，则a+b的最大值是：_____
A: 957B: 64C: 56D: 33
参考答案: B

15、纸上写着2、4、6三个整数，改变其中任意一个，将它改写成为其他两数之和减1，这样继续下去，最后可以得到的是_____。
A: 595、228、368B: 44、95、50C: 103、109、211D: 159、321、163
参考答案: A 本题解释:A。

16、某市财政局下设若干处室，在局机关中不是宣传处的有206人，不是会计处的有177人，已知宣传处与会计处共有41人，问该市财政局共有多少人？_____
A: 218 B: 247 C: 198 D: 212
参考答案: D 本题解释: 【解析】由题意有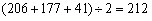：人。所以选D。

17、有下列长度的三条线段，不能组成三角形的是哪一组?_____
A: 4cm、2cm、5cmB: 12cm、14cm、8cmC: 2cm、3cm、4cmD: 6cm、2cm、3cm
参考答案: D 本题解释:D 【解析】三角形两边之和大于第三边;两边之差小于第三边。

18、阳光下，电线杆的影子投射在墙面及地面上，其中墙面部分的高度为1米，地面部分的长度为7米。甲某身高1.8米，同一时刻在地面形成的影子长0.9米。则该电线杆的高度为_____。
A: 12米B: 14米C: 15米D: 16米
参考答案: C 本题解释:【答案】C。解析：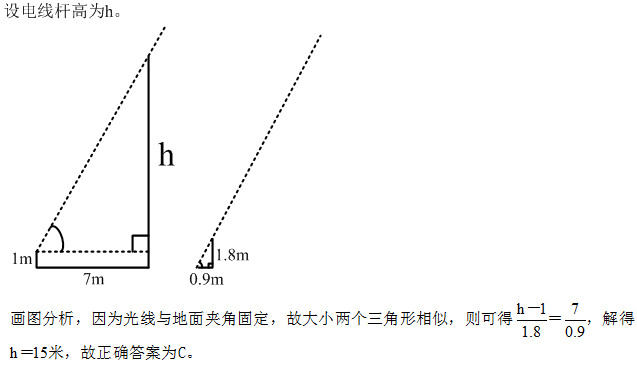

19、A、B两桶中共装有108公斤水。从A桶中取出1/4的水倒入B桶，再从B桶中取出1/4的水倒入A桶，此时两桶中水的重量刚好相等。问B桶中原来有多少公斤水？_____
A: 42B: 48C: 50D: 60
参考答案: D 本题解释:【解析】D。代入排除思想。由题意，最后两桶水中各有54公斤水。代入D项60。则A桶原有水量为48公斤，48×1/4=12,12+60=72,72×1/4=18，72-18=54，满足题意。

20、假设7个相异正整数的平均数是14，中位数是18，则次7个正整数中最大数是多少？_____
A: 58B: 44C: 35D: 26
参考答案: C 本题解释:【答案】C。解析：构造数列问题。此题告诉我们平均数是14，则总和为14*7=98，中位数为18，总共7个数，意味着小于18的有3个数，大于18的有3个数，为了保证最大的数大，所以我们要让大于18的数尽可能的小，则其他的两个数我们可以定义为19，20；所以得到的式子为18+19+20+n<98，所以n<41，则小于41的最大选项为35，所以选择C选项。

21、马场有甲、乙、丙、丁四个入口可以提供人进入游玩，如果现在开了甲、乙两个入口，经过了4．5小时游客全部能够进入，如果开乙、丙两个入口，游客3小时能全部进入，如果开丙、丁两个入口，游客3．5小时全部进入。若只打开甲、丁两个入口，则需要几个小时，游客才能全部进入？_____
A: 63/11B: 63/32C: 196/33D: 172/33
参考答案: A 本题解释:【答案】A。解析：设总人数为1，则开甲、乙两个口，1小时能进入2/9人；开乙、丙两个口，1小时能进入1/3人；开丙、丁两个口，一小时能进入2/7人；三种情况同时存在时，一小时能进入的人数为甲口+乙口+乙口+丙口+丙口+丁口=2（乙口+丙口）+甲口+丁口=2/9+1/3+2/7＝53/63（人）。又因乙口+丙口=1/3（人），所以甲、丁两口同时开放，1小时进入的人数为11/63人。所以只打开甲、丁两个口，游客全部进入，需要的时间是63/11小时。

22、有苹果，桔子各一筐，苹果有240个，桔子有313个，把这两筐水果平均分给一些小朋友，已知苹果分到最后余2个，桔子分到最后还余7个，求最多有多少个小朋友参加分水果？_____
A: 14 B: 17 C: 28 D: 34
参考答案: D 本题解释:【答案】D。解析：240-2=238，313-7=306，此题即要求238和306的最大公约数，238=2×7×17、306=2×3×3×17，可知最大公约数是34。

23、某单位有员工540人，如果男员工增加30人就是女员工人数的2倍，那么原来男员工比女员工多几人？_____
A: 13B: 31C: 160D: 27
参考答案: C 本题解释:【答案】C。解析：男员工增加30人后，总员工为570人，男员工是女员工的2倍，得女员工为570÷3＝190，则原有男员工540－190＝350，男员工比女员工多350－190＝160人。故正确答案为C。老师点睛：男员工增加30人后，总员工为570人，男员工是女员工的2倍，由于540、30均为偶数，则原有男、女员工的数目也为偶数，男员工比女员工多的人数也是偶数。只有选项C符合条件，故正确答案为C。

24、有两个山村之间的公路都是上坡和下坡，没有平坦路。客车上坡的速度保持20千米/小时，下坡的速度保持30千米/小时。现知客车在两个山村之间往返一次，需要行驶4小时。请问这两个山村之间的距离有多少千米?_____
A: 45B: 48C: 50D: 24
参考答案: B 本题解释: 【解析】B。根据平均速度公式可知，全程的平均速度是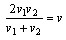：，全程的平均速度是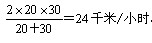：。（已知往返速度，求全程的平均速度，是有简便的算法的，要熟练把握。）两山村之间的路程是：（24×4）2=48千米。

25、下列可以分解为三个质数相乘的最小的三位数是_____。
A: 100B: 102C: 104D: 105
参考答案: B 本题解释:【答案】B。解析：直接代入各选项求解。题目要求找出符合条件的最小的三位数，则从数值较小的选项开始验证。A项，100＝2×2×5×5，不符合题意。B项，102＝2×3×17，符合题意。C、D项的三位数即使可分解为三个质数相乘，数值上也大于B项的102，因此不作考虑。故正确答案为B。

26、今有桃95个，分给甲、乙两个工作组的工人吃，甲组分到的桃有2/9是坏的，其他是好的，乙组分到的桃有3/16是坏的，其他是好的。甲、乙两组分到的好桃共有_____个。
A: 63B: 75C: 79D: 86
参考答案: B 本题解释:【解析】由题意，甲组分到的桃的个数是9的倍数，乙组分到的桃的个数是16的倍数。设甲组分到的桃有9χ个，乙组分到16y个，则9χ+16y=95。可以得到χ=7，y=2，则甲、乙两组分到的好桃共有9×7×（1-2/9）+16×2×1-3/16）=75（个）。故选B。

27、一列快车和一列慢车相对而行，其中快车的车长200米，慢车的车长250米，坐在慢车上的旅客看到快车驶过其所在窗口的时间是6秒钟，坐在快车上的旅客看到慢车驶过其所在窗口的时间是多少秒钟?_____
A: 6秒钟B: 6.5秒钟C: 7秒钟D: 7.5秒钟
参考答案: D 本题解释:【答案解析】解析：追击问题的一种。坐在慢车看快车=>可以假定慢车不动，此时，快车相对速度为V(快)+V(慢)，走的路程为快车车长200;同理坐在快车看慢车，走的距离为250，由于两者的相对速度相同=>250/x=200/6=>x=7.5(令x为需用时间)。

28、某S为自然数，被10除余数是9，被9除余数是8，被8除余数是7，已知100＜S＜1000，请问这样的数有几个？_____
A: 5 B: 4 　 C: 3 　 D: 2
参考答案: D 本题解释:D。【解析】被N除余数是N-1，所以这个数字就是几个N的公倍数-1。10，9，8的公倍数为360n（n为自然数），因为100＜S＜1000，所以有两个数符合条件。

29、现有一个无限容积的空杯子，先加入1克酒精，再加入2克水，再加入3克酒精，再加入4克水，&hellip;&hellip;，如此下去，问最终杯子中酒精溶液浓度为多少?_____ B: 25%C: 33.3%D: 50%
参考答案: D 本题解释:【解析】D。如果把加一次酒精和水看成一个流程，则经过n个流程后，杯子里面有1+3+5+&hellip;+(2n-1)=1/2n(1+2n-1)=n2克酒精，而酒精溶液有1+2+&hellip;+2n=1/2&times;2n(1+2n)=n(1+2n)克。故此时酒精溶液浓度为n2/n(1+2n)=n/(2n+1)，当n趋于无穷大时，溶液浓度趋于1/2=50%。思路点拨：极端法，当加入酒精或水的量极大时连续两次操作水与酒精的差距对整体的影响可以忽略不计，因此必然各占50%。

30、要折叠一批纸飞机，若甲单独折叠要半个小时完成，乙单独折叠需要45分钟完成，若两人一起折叠，需要多少分钟完成?_____
A: 10B: 15C: 16D: 18
参考答案: D 本题解释:答案：D【解析】此题实质上是一道工程问题。设纸飞机总量为1，则甲甲每分钟完成1/30，乙每分钟完成1/45，甲乙共花时间为1/（1/30+1/45）=18。故正确答案应为选项D。

31、某商店将定价为6.25元的笔记本降价20%卖出，结果还获成本25%的利润。笔记本的成本为_____。
A: 5元B: 4元C: 3元D: 2元
参考答案: B 本题解释:B【解析】设成本为x元，计算得x=4。

32、银行存款年利率为2.5%，应纳利息税20%，原存1万元1年期，实际利息不再是250元，为保持这一利息收入，应将同期存款增加到_____元。
A: 15000B: 20000C: 12500D: 30000
参考答案: C 本题解释:C。【解析】令存款为x，为保持利息不变，250=x×2.5%×（1-20%）=>x=12500。

33、教室里有若干学生，走了10名女生后，男生是女生人数的2倍，又走了9名男生后，女生是男生人数的5倍。问：最初有多少名女生?_____
A: 15B: 12C: 10D: 9
参考答案: A 本题解释:A【解析】设最初有x名女生，则男生的数量为2(x-10)，由题意可列等式x-10=5[2(x-10)-9]，可得x=15。故选A。

34、如果某商店 以每打1.8元的价格购进6打小工艺品(每打12件).之后又以每件0.2元卖出.这些小商品全部卖完后商店可得多少利润？_____
A: 32元 B: 3.6元 C: 2.4元 D: 2.84元
参考答案: B 本题解释:B【解析】0.2×12×6-1.8×6=3.6，一打=12个。

35、1898年4月1日，星期五，分别把三个钟调整到相同的时间：12点。第二天中午发现A钟时间完全准确，B钟正好快了1分钟，C钟正好慢了1分钟。现在假设三个钟都没有被调，它们保持着各自的速度继续走而且没有停。那么到_____，三只时钟的时针分针会再次都指向12点。
A: 1900年3月20日正午12点B: 1900年3月21日正午12点C: 1900年3月22日正午12点D: 1900年3月23日正午12点
参考答案: C 本题解释:【答案】C。解析：B钟1天时间快了1分钟，C钟1天时间慢了1分钟，若他们时针分针都再次指向12点，那么，B钟总共快了12小时，同时C钟慢了12小时。那么需要的时间为60×12＝720天，由此，此题变成1898年4月1日的720天后是几月几日的问题。由于1899年跟1900年都为平年，所以两年即730天后为1900年4月1日，往前数10天为3月22日，故正确答案为C。此题要注意闰年的计算方法：公元年数可被4整除（但不可被100整除）为闰年，但是正百的年数必须是可以被400整除的才是闰年，所以1900年是平年。

36、甲、乙两人从400米的环形跑道的一点A背向同时出发，8分钟后两人第三次相遇。已知甲每秒钟比乙每秒钟多行0.1米，那么，两人第三次相遇的地点与A点沿跑道上的最短距离是_____
A: 166米B: 176米C: 224米D: 234米
参考答案: B 本题解释:B.【解析】400-（480×0.1）=352/2=176米。

37、有一块草地，上面的青草每天都生长得一样快。这块草地上的青草供20头牛吃，可以吃12天，或者供25头牛吃，可以吃8天。某人有牛70头，如果要保证青草不被吃完，需要在几块这样的草地上放牧？_____
A: 7B: 8C: 9D: 10
参考答案: A 本题解释:【答案】A。解析：假设这块草地原有草量为x，每天长草量为y，每头牛每天吃草的量为1，则根据公式可得：解得x＝10，这块草地每天的长草量够10头牛吃。要保证青草不被吃完，需要在70÷10＝7（块）这样的草地上放牧。

38、小李用150元钱购买了16元一个的书包、10元一个的计算器和7元一支的钢笔寄给灾区儿童，如果他买的每一样物品数量都不相同，书包数量最多而钢笔数量最少，那么他买的计算器数量比钢笔多多少个?_____
A: 1B: 2C: 3D: 4
参考答案: B 本题解释:B【解析】计算器每个10元，书包每个16元，钢笔每支7元，说明书包的总钱数十钢笔的总钱数=10的倍数。根据题意，钢笔数量最少，当钢笔支数取l时，7元×1=7（元），书包总钱数个位应是3，但16乘以任何数都不可能是3，故舍去。当纲笔支数取2时，7元×2=14（元），书包总钱数的个位数应是6，16乘以l、6个位均可以是6，故根据题意书包数量最多取6。则书包总钱数为16×6=96（元），钢笔总钱数为7×2=14（元），计算器总钱数为150-96-14=40（元），计算器个数为40÷10=4（个），计算器数量比钢笔多4-2=2（个）。

39、画一个边长为2cm的正方形，再以这个正方形的对角线为边画第二个正方形，再以第二个正方形的对角线为边画第三个正方形，则第三个正方形面积为_____平方厘米。
A: 32B: 16C: 8D: 4
参考答案: C 本题解释:C由题可知第2个正方形对角线长为2cm;则第三个正方形的面积为（2）2=8（平方厘米）;正确答案为C。

40、甲、乙两人从400米的环形跑道的一点A背向同时出发，8分钟后两人第三次相遇。已知甲每秒钟比乙每秒钟多行0.1米，那么，两人第三次相遇的地点与A点沿跑道上的最短距离是_____。
A: 166米 B: 176米 C: 224米 D: 234米
参考答案: B

41、一个三位数，各位上的数的和是15，百位上的数与个位上的数的差是5，如颠倒百位与个位上的数的位置，则所成的新数比原数的3倍少39。求这个三位数_____
A: 196B: 348C: 267D: 429
参考答案: C 本题解释: 【解析】C。代入验证，A项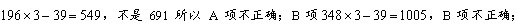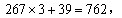符合题意。故选C。

42、某人同时购买2年期、5年期和10年期三种国债，投资额的比为5：3：2。后又以与前次相同的投资总额全部购买5年期国债，则此人两次对5年期国债的投资额占两次总投资的比例的_____。
A: 3/5B: 7/10C: 3/4D: 13/20
参考答案: D

43、一条街上，一个骑车人和一个步行人相向而行，骑车人的速度是步行人的3倍，每个隔10分钟有一辆公交车超过一个行人。每个隔20分钟有一辆公交车超过一个骑车人，如果公交车从始发站每隔相同的时间发一辆车，那么间隔几分钟发一辆公交车？_____
A: 10B: 8C: 6D: 4
参考答案: B 本题解释:B。【解析】设车速V车，人速V人，自行车速3V人，则（V车－V人）×10＝20×（V车－3V人），V车＝5V人，即车走人4倍位移追上人故T＝4×V人×10/5V人＝8。

44、某原料供应商对购买其原料的顾客实行如下优惠措施：①一次购买金额不超过1万元，不予优惠;②一次购买金额超过1万元，但不超过3万元，给九折优惠;③一次购买金额超过3万元，其中3万元九折优惠，超过3万元部分八折优惠。某厂因库容原因，第一次在该供应商处购买原料付款7800元，第二次购买付款26100元，如果他一次购买同样数量的原料，可以少付：_____
A: 1460元B: 1540元C: 3780元D: 4360元
参考答案: A 本题解释:【解析】A。第一次购买原料付款7800元，原料的总价值应为7800元，第二次购买时付款26100元，原料的总价值应为26100&divide;0.9=29000元。如果要将两次购买变成一次购买，则总价值应为7800+29000=36800元，而应该付款额为30000&times;0.9+6800&times;0.8=32440元，一次性购买比分两次购买可以节约7800+26100-32440=1460元。

45、规定两人轮流做一个工程，要求第一个人先做1个小时，第二个人接着做1个小时，然后再由第一个人做1个小时，然后又由第二个人做1个小时，如此反复，做完为止。如果甲、乙轮流做一个工程需要9.8小时，而乙、甲轮流做同样的工程只需要9.6小时，那乙单独做这个工程需要多少小时? _____
A: 6.4B: 7.3C: 8.2D: 9.7
参考答案: B 本题解释:【答案】B。解析：把整个工程看做一个过程，甲乙轮流顺序不一样导致时间不一样，而前面8小时中，两次循环完成的工程是一样的，因此考虑8小时之后的两人的工作效率差。即甲工作2小时相当于乙工作1小时。第一次甲一共做了5小时，换做乙只用2.5小时，即总时间可以节省2.5小时，所以乙单独做只用9.8-2.5=7.3小时。

46、有一个电子钟,每走8分钟亮一次灯,每到整点响一次铃。中午12点整,电子钟响铃又亮灯。下一次既响铃又亮灯是几点钟?_____
A: 1B: 2C: 3D: 4
参考答案: B 本题解释:【答案】B。解析:8分钟和一个小时(60分钟)的最小公倍数是120分钟,所以再过120分钟又一次既响铃又亮灯。

47、一桶农药，加入一定量的水稀释后，浓度为15%;再加入同样多的水稀释，农药的浓度变为12%，若第三次再加入同样多的水，农药的浓度将变为多少?_____
A: 8%B: 10%C: 11%D: 13%
参考答案: B 本题解释:B。【解析】设&delta;加水稀释前农药量为x,?次所加水量为a，所求浓度为y%，则(x+a)15%=(x+2a)12%=(x+3a)y%，解得y%=10%。

48、一袋大白兔奶糖，5块一组分剩余2块，3块一组分剩1块，问这袋糖至少有多少块?_____
A: 26B: 34C: 37D: 43
参考答案: C 本题解释:C【解析】所要求的数必须满足除以5余2，除以3余1，通过代入法，满足条件的只有37，故答案为C。

49、某企业有甲、乙、丙三个部门，已知三个部门员工的人数比为4:5:6，平均年龄是34岁，甲部门员工的平均年龄是30岁，丙部门员工的平均年龄是20岁。问乙部门员工的平均年龄是多少岁?_____
A: 45B: 48C: 51D: 54
参考答案: D 本题解释:D.【解析】这是一道加权平均数问题。设乙部门员工的平均年龄为x岁，则有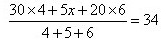<p>具体计算时，x=54。因此，本题的正确答案为D选项。

50、某公司要到外地去推销产品，产品成本为每件3000元。从公司到外地距离是400千米，运费为每件产品每运1千米收1.5元。如果在运输及销售过程中产品的损耗是10%，那么公司要想实现25%的利润率，零售价应是每件多少元? _____
A: 4800B: 5000C: 5600D: 6000
参考答案: B 本题解释:【答案】B。解析：以1件商品为例，成本为3000元，运费为1.5×400=600元，则成本为3000+600=3600元，要想实现25%的利润率，应收入3600×（1+25%）=4500元;由于损耗，实际的销售产品数量为1×（1-10%）=90%，所以实际零售价为每件4500÷90%=5000元。

51、市民广场中有两块草坪，其中一块草坪是正方形，面积为400平方米，另一块草坪是圆形，其直径比正方形边长长10%，圆形草坪的面积是多少平方米？_____
A: 410 B: 400 C: 390 D: 380
参考答案: D 本题解释: 【解析】正方形的边长是20米，那么圆的半径是米，那么圆形草坪的面积是，故选D。

52、100人列队报数，报单数的离队，留下的再依次报数，报单数的再离队，这样重复多次，直到最后只留下一个人，请问此人在第一次报数时是第几号?_____
A: 32B: 50C: 64D: 100
参考答案: C 本题解释:C。第一次报数后，留下队员的号数是：2，4，6，8…96，98，100，均为的倍数;第二次报数后，留下队员的号数是：4，8，12…96，100，均为的倍数;第五次报数之后，留下队员的号数是的倍数;第六次报数之后，留下队员的号数四的倍数可见最后余下的一人在第一次报数时是第64号。

53、在一次有四个局参加的工作会议中，土地局与财政局参加的人数比为5∶4，国税局与地税局参加的人数比为25∶9，土地局与地税局参加人数的比为10∶3，如果国税局有50人参加，土地局有多少人参加？_____
A: 25B: 48C: 60 D: 63
参考答案: C 本题解释: 【解析】根据以上比例关系，可得出土地局︰地税局︰国税局=30︰9︰25，所以土地局有60人参加。所以选C。

54、一个长方形，它的周长是32米，长是宽的3倍。这个长方形的面积是多少平方米?_____
A: 64B: 56C: 52D: 48
参考答案: D 本题解释:D设宽为x则长为3x，则2(x+3x)=32，则x=4，故面积为48平方米。

55、黎明对张伟说：当我的岁数是你现在的岁数时，你是4岁；张伟对黎明说：当我的岁数是你现在的岁数时。你是67岁。问黎明、张伟现在多少岁？_____
A: 45岁、26岁B: 46岁、25岁C: 47岁、24岁D: 48岁、23岁
参考答案: B 本题解释:根据选项可知黎明比张伟大。设二者年龄差为x，那么张伟今年是4＋x岁，黎明为4＋2x岁。当张伟是黎明现在的岁数时，黎明是4＋3x岁。因此，4＋3x＝67，x＝21。张伟今年4＋21＝25岁，黎明25＋21＝46岁。

56、除以5余1，b除以5余4，如果3a >b，那么3a-b除以5余几? _____
A: 1B: 2C: 3D: 4
参考答案: D 本题解释:D【解析】3a 除以5 应余1×3=3，已知b 除以5 余4，则3a-b 除以5 余3-4+5=4。故选D。

57、某校学生列队以8千米/小时的速度前进，在队尾，校长让一名学生跑步到队伍的最前面找带队的老师传达一个命令，然后立即返回队尾，这位学生的速度为12千米/小时，从队伍出发赶到排头又回到队尾共用了7.2分钟，那么学生的队伍长_____米。
A: 360B: 400C: 450D: 500
参考答案: B 本题解释:B【解析】8千米/小时=（400/3）米/分，12千米/小时=200米/分，设队伍长χ米，则χ÷（200-400/3）+χ÷（200+400/3）=7.2，解得χ=400。

58、妈妈给了红红一些钱去买贺年卡，有甲、乙、丙三种贺年卡，甲种卡每张0.50元，丙种卡每张1.20元。用这些钱买甲种卡要比买乙种卡多买8张，买乙种卡要比买丙种卡多买6张。妈妈给了红红多少钱?_____
A: 8元B: 10元C: 12元D: 15元
参考答案: C 本题解释:【解析】：盈亏总额为0.5×8+1.2×6=11.2（元），单价相差1.2-0.5=0.7（元），所以共可买乙种卡11.2÷0.7=16（张）。妈妈给了红红0.5×（16+8）=12（元）。故本题正确答案为C。

59、10个连续偶数的和是以1开始的10个连续奇数和的2.5倍，其中最大的偶数是多少?
A: 34B: 38C: 40D: 42
参考答案: A 本题解释:【答案】A。解析：猜证结合，以1开始的10个连续奇数的和是250，代入答案中得A。

60、某A、B、C三地的地图如下图所示，其中A在C正北，B在C正东，连线处为道路。如要从A地到达B地，且途中只能向南、东和东南方向行进，有多少种不同的走法（）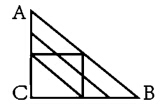
A: 9B: 11C: 13D: 15
参考答案: D 本题解释:【答案】D。解析：从A点出发从上向下总共4个路口，按照题目要求，第一个路口到B地有3种走法；第二个路口在第一个路口路线基础上加了2种走法，共5种走法；第三个路口在第二个路口路线的基础上又加了一条路线，共6种走法；最后一个路口只有一个走法。所有总计15种走法。

61、小王的手机通讯录上有一手机号码，只记下前面8个数字为15903428。但他肯定，后面3个数字全是偶数，最后一个数字是6，且后3个数字中相邻数字不相同，请问该手机号码有多少种可能?_____
A: 15B: 16C: 20D: 185
参考答案: B 本题解释:【答案】B。解析：一位偶数有0、2、4、6、8，共5个。考虑倒数第二位，因为相邻数字不相同且为偶数，则有4种选择。倒数第三位与倒数第二位不相同，也有4种选择，共有4×4=16种情况。

62、一本100多页的书，被人撕掉了4张.剩下的页码总和为8037。则该书最多有多少页_____
A: 134B: 136C: 138D: 140
参考答案: A 本题解释:【答案】A。解析：撕掉四张纸的页码数之和是偶数，由剩下页码数是奇数可知总的页码数是奇数，排除B、D。若为C，则撕掉的页码数之和是138×（138+1）÷2—8037=1554>138×8，矛盾。A项符合题意。

63、超市经理为某商品准备了两种促销方案，第一种是原价打7折；第二种是买二件赠一件同样商品。经计算，两种方案每件商品利润相差0.1元，若按照第一种促销方案，则100元可买该商品件数最大值是_____
A: 33B: 47C: 49D: 50
参考答案: B 本题解释:【答案】B。解析：设该商品原价为x，则第一种方案下，三件促销价格为2.1x，第二种方案下，三件促销价格2x，两种方案差价为0.1x。根据题意，两种方案每件商品的利润差为0.1元，则三件商品差价0.3元，即0.1x=0.3，解得x=3元，那么按照第一种促销方案，商品售价2.1元，100元最多可以购买该商品47件，选择B项。

64、有14个纸盒，其中有装1只球的，也有装2只和3只球的。这些球共有25只，装1只球的盒数等于装2只球和3只球的盒数之和。装3只球的盒子有多少个?_____
A: 7B: 5C: 4D: 3
参考答案: C 本题解释: C【解析】设装有3只球的盒子有x个，装有2只球的盒子有y个，则装有1只球的盒子有（x+y）个。由题意可得：x+y+（x+y）=14（x+y）+3x+2y=25故x=4,y=3。

65、一列火车通过一条长1140米的桥梁(车头上桥至车尾离桥)用50秒，火车穿越长1980米的隧道用80秒，则这列火车车身是_____米。
A: 260 B: 270 C: 360 D: 380
参考答案: A 本题解释:A。设列车车身长B米，则列出方程为（1140+B）/50=（1980+B）/80，解出方程为B=260米。所以正确答案为A项。

66、一个袋子里放着各种颜色的小球，其中红球占1/4，后来又往袋子里放了10个红球，这时红球占总数的2/3，问原来袋子里有多少个球?_____
A: 8B: 12C: 16D: 20
参考答案: A 本题解释: A 解析：设原来有小球a个，则有：（a/4+10）÷（a+10）=2/3，解得a=8，选A。

67、某班有50位同学参加期末考试，结果英文不及格的有15人，数学不及格的有19人，英文和数学都及格的有21人。那么英文和数学都不及格的有_____人。
A: 4B: 5C: 13D: 17
参考答案: B 本题解释:本题正确答案为B。解析：设英文和数学都不及格的有x人，由容斥原理可得15+19-x=50-21，得x=5,故选B。

68、A、B两地以一条公路相连。甲车从A地，乙车从B地以不同的速度沿公路匀速率相向开出。两车相遇后分别掉头，并以对方的速率行进。甲车返回A地后又一次掉头以同样的速率沿公路向B地开动。最后甲、乙两车同时到达B地。如果最开始时甲车的速率为X米/秒，则最开始时乙车的速率为（）。
A: 4X米/秒B: 2X米/秒C: 0.5X米/秒D: 无法判断
参考答案: B 本题解释:答案：B。显然最初乙的速度较快，由题意知，以甲车的速率走完了一遍全程，以乙车的速率走了两遍全程，所费时间相等，故乙车速度为甲车两倍。

69、某地区水电站规定，如果每月用电不超过24度，则每度收9分钱；如果超过24度，则多出度数按每度2角收费，若某月甲比乙多交了9.6角，则甲交了几角几分？_____
A: 27角6分B: 26角4分C: 25角5分D: 26角6分
参考答案: A 本题解释:【解析】A。如果每月用电24度，则应该交24×9＝216分钱，即21.6角。答案中没有这个答案，就是说甲已经超过了这个规定数字。设他用了24＋M度电，则交了24×9+M×20＝216＋20×M，甲比乙多交了96分，则216＋20×M－96可以被9整除，即（20×M+120）÷9。M＝3时，（20×M＋120）÷9＝2，即甲用了27度电，用了276分。

70、一个两位数除以一个一位数，商仍是两位数，余数是8。问：被除数、除数、商以及余数之和是多少? _____
A: 98B: 107C: 114D: 125
参考答案: D 本题解释:【答案】D。解析：猜证结合的98÷10=9余8，10+98+9+8=125。

71、某数的百分之一等于0.003，那么该数的10倍是多少?_____。
A: 0.003B: 0.03C: 0.3D: 3
参考答案: D 本题解释:D【解析】某数的百分之一为0.003，则该数为0.3，那么它的10倍为3。故正确答案为D。

72、将一个正方形分成9个小正方形，填上1到9这9个自然数，使得任意一个横行，一个纵列以及每一对角线上的3个数之和等于15，请问位于中间的小正方形应填哪个数?_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释: 【解析】B。欲保证3个数之和都等于15，只有中间的数字为平均数5才可。

73、某单位职工24人中，有女性11人，已婚的有16人。已婚的16人中有女性6人。问这个单位的未婚男性有多少人?_____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释: B 解析：由题意：未婚共有：24-16=8人，其中未婚女性有：11-6=5人，故未婚男性有：8-5=3人，选B。

74、1-2+3-4+5-6+7-8+…+1989-1990+1991=_____
A: 895 B: 896 C: 995 D: 996
参考答案: D 本题解释: D。原式可等于1+1990/2=996。故正确答案为D。

75、有一串数：1，3，8，22，60，164，448，……其中第一个数是1，第二个数是3，从第三个数起，每个数恰好是前两个数之和的2倍。那么在这串数中，第2000个数除以9的余数是_____
A: 1B: 2C: 3D: 4
参考答案: B 本题解释:B。【解析】本题属于组合数列。奇数项：-1，4，14，29，();偶数项：1，8，20，37，两两做差：5，10，157，12，17两数列均为二级等差数列，于是得到所求项为20+29=49。所以选择B选项。

76、某工厂11月份工作忙，星期六、日不休息，而且从第一天开始，每天下班后都从总厂陆续派相同人数的工人到分厂工作，直到月底下班后，总厂还剩工人238人。如果月底统计总厂工人的工作量是8070个工作日(1人工作1天为1个工作日)，且无1个缺勤，那么，这个月由总厂派到分厂工作的工人共多少人？_____
A: 46人B: 30人C: 60人D: 62人
参考答案: C 本题解释:11月份有30天。设每天下班后派往分厂的人数为2，则根据题意可知，最后一天总厂的工作量为238+z，可列方程238+x+238+2x+…+238+30x=8070，解得x=2，即每天派2人到分厂工作，11月份30天共派了60人到分厂。故答案为C。

77、甲容器有浓度为3%的盐水190克，乙容器中有浓度为9%的盐水若干克，从乙取出210克盐水倒入甲，甲容器中的盐水的浓度是多少? _____
A: 5.45%B: 6.15%C: 7.35%D: 5.95%
参考答案: B 本题解释: B。根据两溶液混合公式可得，3%×190+9%×210=（190+210）×C，解得C=6.15%。故正确答案为B。

78、一次象棋比赛共有10名选手参加，他们分别来自甲、乙、丙三个队，每个人都与其余九名选手各赛一盘，每盘棋的胜利者得1分，负者得0分，平局各得0.5分。结果甲队选手平均得4.5分，乙队选手平均得3.6分，丙队选手平均得9分，那么甲、乙、丙三队参加比赛的选手的人数依次是_____。
A: 6人、3人、1人B: 4人、5人、1人C: 3人、5人、2人D: 5人、1人、4人
参考答案: B 本题解释:B【解析】根据10名选手参加比赛，取胜者得1分，而丙队选手平均得分9分，这样丙队参赛选手只能是1人，且与其余9名选手比赛中应全部获胜。又根据每盘赛棋中胜者得1分，负者0分，平局各得0.5分，可知各队得分总数应是整数或小数部分的十位上是5，现乙队选手平均得3.6分，十位上是6，同样，甲、乙两队共有9人参赛，这样乙队参赛选手肯定是5人。因此甲队参赛选手人数是4人，乙队参赛选手人数是5人，丙队参赛选手人数是1人。

79、6个空瓶可以换一瓶汽水，某班同学喝了157瓶汽水，其中有一些是用喝剩下来的空瓶换的，那么他们至少要买多少瓶汽水？_____
A: 131 B: 130 C: 128 D: 127
参考答案: A 本题解释: 【解析】A。131÷5×6=157.2（取整）=157。

80、在一次展览会上，展品上有366部手机不是A公司的，有276部手机不是B公司的，但两公司的展品共有378部。问B公司有多少部手机参展？_____
A: 134B: 144C: 234D: 244
参考答案: C 本题解释:C。其它公司的有（366+276-378）/2=132部，所以B公司有366-132=234，选C。

81、反事实思维通常是在头脑中对已经发生了的事件进行否定，然后表现为原本可能发生但现实并未发生的心理活动。根据发生的方向可将反事实思维分为上行反事实思维和下行反事实思维。上行反事实思维，是对于过去已经发生了的事件，想象如果满足某种条件，就有可能出现比真实结果好的结果；下行反事实思维，是对过去已经发生了的事件，想象如果满足某种条件，就有可能出现比真实结果坏的结果。根据上述定义，下列各项中属于下行反事实思维的是_____。
A: 要是当时好好复习，这次考试就可以通过了B: 如果我发挥的稍微差一点，就与奖牌失之交臂了C: 如果祖父还活着，他一定不愿意看到今天这个局面D: 如果没有带这么多东西的话，我们现在就可以跑的快点了
参考答案: B 本题解释:【答案】B。解析：本题是定义判断，是一道双定义题，讲反事实思维，后又延生出上行反事实思维和下行反事实思维，而问题问的是哪个选项是属于下行反事实思维，反事实思维的意思是对过去发生的事情，要是满足某种条件就会发生比真实结果坏的事，A、C、D答案都是没有出现一个坏的结果，只有B答案出现了一个比预期坏的结果。所以B为正确答案。

82、某网站针对年底上映的两部贺岁电影进行调查，在接受调查的160人中，看过《未来警察》的有91人，看过《杜拉拉升职记》的有59人，22人两部电影都看过，那么，两部电影都没看过的有多少人?_____
A: 32人B: 12人C: 42人D: 10人
参考答案: A 本题解释: A 解析：设两部电影都没看过的有x人，依题意可得：91+59-22+x=160，解得x=32。即有32人两部电影都没看过，答案为A。

83、林文前年买了8000元的国家建设债券，定期3年。到期他取回本金和利息一共10284.8元。这种建设债券的年利率是多少？_____
A: 9.52% B: 9.6% C: 8.4% D: 9.25%
参考答案: A 本题解释:A【解析】求利息的公式：利息=本金×利率×时间，可得出：利率=利息÷时间÷本金。而他3年所得的利息是：10284.8-8000=2284.8（元）；这样即可求出这债券的年利率是多少。（10284.8-8000）÷3÷8000=2284.8÷3÷8000=761.6÷8000=0.0952=9.52%

84、1～100各数所有不能被9整除的自然数的和是_____。
A: 217B: 594C: 5050D: 4456
参考答案: D 本题解释:D解析：在1至100中，被9整除的数的和是9+18+27+…+99=9×(1+2+3+…+11)=9×66=5941至100各数之和是1+2+3+…+100=100(1+100)2=5050所以在1至100的各数中，所有不能被9整除的数的和是5050-594=4456。因此，本题正确答案为D。

85、将一个正方形分成9个小正方形，填上1到9这9个自然数，使得任意一个横行，一个纵列以及每一对角线上的3个数之和等于15，请问位于中间的小正方形应填哪个数?_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:答案：B【解析】欲保证3个数之和都等于15，只有中间的数字为平均数5才可。

86、某小学五年级同学分成69个小组，每组3人，去参加植树劳动。在这些小组中，只有1名男同学的共有15个小组，至少有2名女同学的共有36个小组，有3名男同学的小组与有3名女同学的小组同样多。问这所小学五年级共有男同学多少名?_____
A: 102B: 136C: 144D: 158
参考答案: A 本题解释:【解析】A。有1名男生2名女生的小组有15个，则有3名女生的小组有36-15=21个，所以有3名男生的小组也有21个，只有1名女生的小组有69-15-21-21=12个，故男生一共有15+12×2+21×3=102名。

87、某人用4 410元买了一台电脑，其价格是原来定价相继折扣了10％和2％后的价格，则电脑原来定价是_____。
A: 4 950元 B: 4 990元C: 5 000元 D: 5 010元
参考答案: C

88、甲、乙两时钟都不正确，甲钟每走24小时，恰好快1分钟;乙钟每走24小时，恰好慢1分钟。假定今天下午三点钟的时候，将甲、乙两钟都调好，指在准确的时间上，任其不停地走下去，问下一次这两只钟都同样指在三点时，要隔多少天?_____
A: 30B: 240C: 480D: 720
参考答案: D 本题解释:【答案解析】可以先求出甲钟比标准时钟多转一圈所需天数，标准时钟比乙钟多走一圈所需天数，然后再求二者的最小公倍数。甲钟与标准时钟下一次同时指向三点时，甲钟比标准时钟多转一圈，也就是多走12小时，即60×12分钟，需要60×12÷(61-60)=720÷1=720(天)同样，标准时钟与乙钟下一次同时指向三点时，标准时钟比乙钟多转一圈，需要60×12÷(60-59)=720÷1=720(天)所以，经过720天后，甲、乙两钟同时指在三点。故正确答案为D。

89、有水果糖、奶糖、巧克力三袋重量不同的糖果，水果糖与奶糖的重量比是6：5，若水果糖的2/3被吃掉，且被吃掉的水果糖与被吃掉的巧克力的重量之比是5：4，那么这两种糖剩下的部分重量相等。问原先水果糖、奶糖、巧克力的重量之比是多少？_____
A: 35：30：31B: 25：20：21C: 30：25：26D: 42：35：40
参考答案: C 本题解释:C。

90、某单位有青年员工85人，其中68人会骑自行车，62人会游泳，既不会骑车又不会游泳的有12人，则既会骑车又会游泳的有_____人。
A: 57B: 73C: 130D: 69
参考答案: A 本题解释:【解析】68+62+12-85=57人。

91、一种商品如果以八折出售，可以获得相当于进价20%的毛利，那么如果以原价出售，可以获得相当于进价百分之几的毛利?_____
A: 20%;B: 30%;C: 40%;D: 50%;
参考答案: D 本题解释:【答案解析】：选D，设原价X，进价Y，那X×80%-Y=Y×20%,解出X=1.5Y所求为[(X-Y)/Y]×100%=[(1.5Y-Y)/Y]×100%=50%

92、用一个尽量小的自然数乘以1999，使其乘积的尾数出现六个连续的9，求这个乘积。_____
A: 5999999B: 4999999C: 3999999D: 2999999
参考答案: C 本题解释:【答案】C。解析：解析1：将各项代入检验，只有3999999能被1999整除，故正确答案为C。解析2：1999＝2000－1，2001＝2000＋1，因此1999×2001＝(2000－1)×(2000＋1)＝2000×2000－1＝3999999。故正确答案为C。

93、计算19961997×19971996-19961996×19971997的值是_____。
A: 0B: 1C: 1 0000D: 100
参考答案: C 本题解释:C【解析】原式=(19961996+1)×19971996-19961996×(19971996+1)=19971996-19961996=10000

94、有20名工人修筑一段公路，计划15天完成。动工3天后抽出5人去其他工地，其余人继续修路。如果每人工作效率不变，那么修完这段公路实际用_____
A: 19天B: 18天C: 17天D: 16天
参考答案: A 本题解释:【答案】A。解析：5人12天完成的工作量分配给15人需要5×12÷15=4天完成，所以修完这段公路实际用15+4=19天。

95、有a、b、c三个数，已知a×b=24，a×c=36，b×c=54，求a+b+c=_____
A: 23B: 21C: 19D: 17
参考答案: C 本题解释: C 解析：此题最好用猜证结合法。试得a、b、c分别为：4、6、9，故选C。若要正面求解：则由前两个式子可得b=2c/3，代入第三个式子可得c=9，进而求得a=4，b=6。,a2=24×36÷54=16，所以a=4，则b=6，c=9，故a+b+c=19。

96、一果农想将一块平整的正方形土地分割为四块小土地，并将果树均匀整齐地种在土地的所有边界上，且在每块土地的四个角上都种上一棵果树，该果农未经细算就购买了60颗果树，如果仍按上述想法种植，那他至少多买了_____棵果树。 B: 3C: 6D: 15
参考答案: B 本题解释:【答案解析】本题可利用整除特征性求解，分割成4个小正方形后共有9个顶点，12条边，设每条边(不算顶点)种x棵树，则可种12x+9棵，使总棵树小于60的最大x为4，此时可种57棵树，剩余3棵，所以正确答案为B项。

97、甲、乙两人进行乒乓球比赛，比赛采取三局两胜制，无论哪一方先胜两局则比赛结束。甲每局获胜的概率为2/3，乙每局获胜的概率为1/3。问甲最后取胜的概率是多少?_____
A: AB: BC: CD: D
参考答案: A

98、某中学给住校生分配宿舍，如果每个房间住3人，则多出20人，如果每个房间住5人，则有2间没人住，其他房间住满。则总共有多少人是住校生？_____
A: 60B: 65C: 70D: 75
参考答案: B 本题解释:【答案】B。解析：显然在每间房3人的基础上增加2人，不仅包括了多出的人，还包括了空出的2间共10人，因此房间数为30÷2＝15（间），因此总人数为15×3+20＝65（人）。

99、大小两个数的和是50.886，较大数的小数点向左移动一位就等于较小的数，求较大的数是_____。
A: 46.25B: 40.26C: 46.15D: 46.26
参考答案: D 本题解释:【答案】D。解析：观察选项发现，大数小数点后有两位，因为大小两个数的和是50.886，说明小数小数点后应该有三位，并且尾数为6，排除A、C选项。B选项，40.26小数点左移一位变为4.026，40.26+4.026=44.286≠50.886，排除B选项。D选项，46.26小数点左移一位变为4.626，46.26+4.626=50.886，因此，本题答案为D选项。

100、某社团共有46人，其中36人爱好戏剧，30人爱好体育，38人爱好写作，40人爱好收藏，问这个社团至少有_____人以上四项活动都喜欢。
A: 5B: 6C: 7D: 8
参考答案: B 本题解释:【答案解析】根据题意可知，不爱好戏剧的有46-36=10人，不爱好体育的有46-30=16人，不爱好写作的有46-38=8人，不爱好收藏的有46-40=6人。要使四项活动都喜欢的人最少，则应使不爱好这四项活动的人最多，即使不爱好这四项活动的人均不重复，所以至少有46-(10+16+8+6)=6人四项活动都喜欢。所以正确答案为B项。