1、1至1000中所有不能被5、6、8整除的自然数有多少个?_____
A: 491B: 107C: 400D: 600
参考答案: D 本题解释: D【解析】 只要求出1～1000内5的倍数、6的倍数或8的倍数或5×6，5×8，24，120的倍数，再根据容斥原理就可求得5的倍数有5、10……1000共200个6的倍数有6、12……996共166个8的倍数有8、16……共125个24的倍数有24、48……984共41个30的倍数有30、60……990共33个40的倍数有40、80……1000共25个120的倍数有120、240……960共8个根据容斥原理可知，5或6或8的倍数有（200+166+125）-（33+25+41）+8=400（个）不能被5或6或8中任一个整除的有1000-400=600（个）故本题选D。

2、有10个优秀名额，分别分给3个科室，且科室一至少分1个名额，科室二至少分2个名额，科室三至少分3个名额，问有多少种分配方案?_____
A: 10B: 15C: 20D: 30
参考答案: B 本题解释:B.【解析】这是一道排列组合问题。先拿出3个名额，分别给科室二和科室三1个和2个名额，剩下的7个名额分给三个科室，每个科室至少一个名额，可用插板法求解，在6个空格中插入2个插板则分配方法有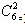<p>15种分法，因此，本题的正确答案为B选项。

3、某市夏季高峰期对居民用电采用如下办法收取电费：用户月用电量在50度以内的部分，按0.4元/度收费;超过50度的部分，按0.8元/度收费。该市一户居民去年夏季高峰期有一个月的电费为32元，那么这个月该用户用电度数是_____。
A: 50度B: 55度C: 60度D: 65度
参考答案: D

4、出租车在7公里以内收费10.6元(不足7公里按7公里收费)，以后每走1公里收费1.8元，某乘客有一次乘出租车花了34元，他乘坐了多少公里?_____
A: 16B: 17C: 20D: 23
参考答案: C 本题解释:C解析：设他乘坐了x公里，根据题意列方程，得：10.6+(x-7)×1.8=34，解得：x=20，选C。

5、现有式样、大小完全相同的四张硬纸片，上面分别写了1、2、3、4四个不同的数字，如果不看数字，连续抽取两次，抽后仍旧放还，则两次都抽到2的概率是_____。
A: 1/2B: 1/4C: 1/8D: 1/16
参考答案: D 本题解释:【解析】两次都抽到2的概率是1/4*1/4=1/16，选D。

6、A、B、C三件衬衫的总价格为520元，分别按9.5折，9折，8.75折出售，总价格为474元，A、B两件衬衫的价格比为5﹕4，A、B、C三件衬衫的价格分别是多少元?（）
A: 250，200，70B: 200，160，160C: 150，120，250D: 100，80，340
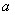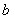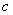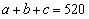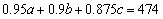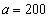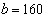参考答案: B 本题解释:设A，B，C三件衬衫的价格分别为，，，则可以列方程组：，，，解得，，，所以选B。

7、某数除以11余8，除以13余10，除以17余12，那么这个数的最小可能值是_____
A: 140B: 569C: 712D: 998
参考答案: D 本题解释:D。选项中只有998加上3能整除11和13，加上5能整除17。

8、在同一环形跑道上小陈比小王跑得慢，两人都按同一方向跑步锻炼时，每隔12分钟相遇一次；若两人速度不变，其中一人按相反方向跑步，则隔4分钟相遇一次。问两人跑完一圈花费的时间小陈比小王多几分钟？_____
A: 5B: 6C: 7D: 8
参考答案: B 本题解释:不妨设小王和小陈速度分别为x，y，跑道长度为s，则：两人都按同一方向跑步锻炼时，每隔12分钟相遇一次，说明s/（x—y）=12;若两人速度不变，其中一人按相反方向跑步，则每隔4分钟相遇一次，说明s/（x+y）=4;解得s=6x=12y，所以两人跑完一圈花费的时间小陈比小王多6分钟。

9、有一些水管，它们每分钟注水量都相等。现在打开其中若干根水管，经过预定时间的1/3，再把打开的水管增加1倍，就能按预定时间注满水池。如果开始打开10根水管，中途不增加水管，也能按预定时间注满水池。则最开始打开’了_____根水管。
A: 5B: 6C: 7D: 8
参考答案: B 本题解释:【解析】增开水管后，有原来2倍的水管，注水时间是预定时间的1-1/3=2/3，2/3是1/3的2倍，因此增开水管后的这段时间的注水量，是前一段时间注水量的4倍。设水池容量是1，预定时间的1/3（前一段时间）的注水量是1—4/（1+4）=1/5，10根水管同时打开能按预定时间注满水池，每根水管的注水量是1/10，预定时间的1/3每根水管的注水量是1/10×1/3=1/30，1/5÷1/30=6根。

10、甲乙两个乡村阅览室，甲阅览室科技类书籍数量的1/5相当于乙阅览室该类书籍的1/4，甲阅览室文化类书籍数量的2/3相当于乙阅览室该类书籍的1/6，甲阅览室科技类和文化类书籍的总量比乙阅览室两类书籍的总量多1000本，甲阅览室科技类书籍和文化类书籍的比例为20:1，问甲阅览室有多少本科技类书籍?_____
A: 15000B: 16000C: 18000D: 20000
参考答案: D 本题解释:答案：D.[解析]假设甲阅览室科技类书籍有20x本，文化类书籍有x本，则乙阅读室科技类书籍有16x本，文化类书籍有4x本，由题意有：（20x+x）-（16x+4x）=1000，解出x=1000，则甲阅览室有科技类书籍20000本。

11、黑色、黄色、白色的筷子各10根摆放在一起，黑暗中想从这些筷子中取出颜色不同的两双筷子，至少要拿出多少根?_____
A: 12B: 13C: 14D: 11
参考答案: B 本题解释:B 解析：最不利的情况是，取出了10根颜色相同的筷子，又从剩下的两种颜色的筷子中各取了1根，现在再任取1根，就能保证至少有两双不同颜色的筷子。即10+1+1+1=13（根）。故本题答案为B。

12、心灵投射谬误也称为投射作用，它是一种非形式谬误，有两种形式，一种形式是某人认为他看世界的观点反映了世界的真相。也就是，某人将他的个人感觉投射到真实世界；另一种形式是某人认为自己不了解一个现象意味着这现象无法被理解或不是真的。根据上述定义，下列不属于心灵投射谬误的是_____。
A: 小李忍受不了闻臭豆腐的味道，就说臭豆腐这么臭，没人会喜欢吃B: 小敏是重庆人，到上海工作后，他发现上海菜普遍是甜的，于是他逢人就说上海菜很难吃C: 尽管知道葡萄架上的葡萄很甜，但是小刘因为摘不到，就对别人说葡萄很酸D: 课间，小荣给大家讲了一个冷笑话，小明理解不了为什么大家听后都捧腹大笑，就说小荣讲的笑话一点水平都没有
参考答案: C 本题解释:【答案】C。解析：心灵投射谬误有两种形式，一种是强调自己的主观意识，即认为自己的观点就是事情的真相。另一种认为自己不了解的就是无法理解的或不是真的。C项小刘的行为是自欺欺人的表现，他对别人说葡萄很酸，但自己并没有认为葡萄是酸的，因为他知道葡萄很甜，不符合“心灵投射谬误”的定义，故本题选C。

13、11338×25593的值为：_____
A: 290133434B: 290173434C: 290163434D: 290153434
参考答案: B 本题解释:答案：B 解析：由于25593为3的倍数，故最后的结果一定能够被3整除，分析选项，只有B符合。

14、12个啤酒空瓶可以免费换1瓶啤酒，现有101个啤酒空瓶，最多可以免费喝到的啤酒为_____。
A: 8瓶B: 9瓶C: 10瓶D: 11瓶
参考答案: B 本题解释:B。12空瓶＝1空瓶＋瓶中酒，因此11空瓶＝瓶中酒。101个空瓶最多喝到[101÷111＝9瓶啤酒（[]为取整号）。

15、从装满1000克浓度为50%的酒精瓶中倒出200克酒精，再倒入蒸馏水将瓶加满。这样反复三次后，瓶中的酒精浓度是多少_____
A: 22.5%B: 24.4%C: 25.6%D: 27.5%
参考答案: C 本题解释:【解析】C。每次操作后，酒精浓度变为原来的，因此反复三次后浓度变为。

16、6个空瓶可以换一瓶汽水，某班同学喝了157瓶汽水，其中有一些是用喝剩下来的空瓶换的，那么他们至少要买多少瓶汽水？_____
A: 131 B: 130 C: 128 D: 127
参考答案: A 本题解释: 【解析】A。131÷5×6=157.2（取整）=157。

17、一批布料，全部用来做上衣可做60件，全部用来做裤子可做40条，现在做上衣、裤子、裙子各5件，恰好用去全部布料的1/4，剩下布料全部做裙子，则还可以做多少条?_____
A: 80B: 90C: 100D: 110
参考答案: B 本题解释:B【解析】设布料总量为120单位，则每件上衣需2单位布料，每条裤子需3单位布料，又上衣、裤子、裙子各做5件，用去︰120×1/4=30单位，所以每条裙子需1单位布料，则可再生产裙子︰(l20-30)÷1=90(条)，故答案为B选项。

18、18名游泳运动员，有8名参加仰泳，有10名参加蛙泳，有12名参加自由泳，有4名既参加仰泳又参加蛙泳，有6名既参加蛙泳又参加自由泳，有5名既参加仰泳又参加自由泳，有2名这3个项目都参加。这18名游泳运动员中，只参加1个项目的有多少名?_____
A: 5B: 6C: 7D: 4
参考答案: B 本题解释: 【解析】B。利用文氏图可以迅速准确地求得答案。注意本题目的陷阱，18名运动员并不是都参加了项目。由图可知;只参加一个项目的有l+2=3=6名。

19、甲乙二人分别从相距若干公里的A、B两地同时出发相向而行，相遇后各自继续前进，甲又经1小时到达B地，乙又经4小时到达A地，甲走完全程用了几小时? _____
A: 2B: 3C: 4D: 6
参考答案: B 本题解释:B【解析】这个题目只要抓住固定不变的部分，不管时间怎么变速度比是不变的。假设相遇时用了a小时那么甲走了a小时的路程 乙需要4小时根据速度比=时间的反比则V甲：V乙=4 ：a那么乙走了a小时的路程 甲走了1小时还是根据速度比=时间的反比则 V甲：V乙=a ：1即得到 4：a=
A:1a=2所以答案是甲需要1+2=3小时走完全程。

20、某原料供应商对购买其原料的顾客实行如下优惠措施：①一次购买金额不超过1万元，不予优惠;②一次购买金额超过1万元，但不超过3万元，给九折优惠;③一次购买金额超过3万元，其中3万元九折优惠，超过3万元部分八折优惠。某厂因库容原因，第一次在该供应商处购买原料付款7800元，第二次购买付款26100元，如果他一次购买同样数量的原料，可以少付：_____
A: 1460元B: 1540元C: 3780元D: 4360元
参考答案: A 本题解释:【解析】A。第一次购买原料付款7800元，原料的总价值应为7800元，第二次购买时付款26100元，原料的总价值应为26100&divide;0.9=29000元。如果要将两次购买变成一次购买，则总价值应为7800+29000=36800元，而应该付款额为30000&times;0.9+6800&times;0.8=32440元，一次性购买比分两次购买可以节约7800+26100-32440=1460元。

21、(1.2)2+(1.3)2+(1.4)2+(1.5)2的值是_____。
A: 6.30 B: 6.49 C: 7.56 D: 7.34
参考答案: D 本题解释:D。本题可采用尾数法，（1.2）2尾数为4，（1.3）2尾数为9，（1.4）2尾数为6，（1.5）2尾数为5，4+9+6+5尾数为4，所以正确答案为D项。

22、某校学生列队以8千米/小时的速度前进，在队尾，校长让一名学生跑步到队伍的最前面找带队的老师传达一个命令，然后立即返回队尾，这位学生的速度为12千米/小时，从队伍出发赶到排头又回到队尾共用了7.2分钟，那么学生的队伍长_____米。
A: 360B: 400C: 450D: 500
参考答案: B 本题解释:B【解析】8千米/小时=（400/3）米/分，12千米/小时=200米/分，设队伍长χ米，则χ÷（200-400/3）+χ÷（200+400/3）=7.2，解得χ=400。

23、某单位举办庆国庆茶话会，买来4箱同样重的苹果，从每箱取出24千克后，结果各箱所剩的苹果重量的和，恰好等于原来一箱的重量。那么原来每箱苹果重多少千克?_____
A: 16B: 24C: 32　D: 36
参考答案: C 本题解释:【答案】C。解析：取出4×24=96千克苹果，相当于4-1=3箱的重量，则原来每箱苹果重96÷3=32千克。

24、蜘蛛有8条腿，蜻蜓有6条腿和2对翅膀，蝉有6条腿和1对翅膀，现在这三种小虫共18只，有118条腿和18对翅膀，蜘蛛，蜻蜓，蝉各几只_____
A: 5、5、8B: 5、5、7C: 6、7、5D: 7、5、6
参考答案: A 本题解释:【答案】A。解析：这是道复杂的“鸡兔同笼”问题，首先，蜻蜓和蝉都是6条腿，数腿的时候可以放在一起考虑，因此蜘蛛有（118—6×18）÷（8—6）=5只，因此蜻蜓和蝉共有18—5=13只，从而蜻蜓有（18—1×13）÷（2—1）=5只，蝉有13—5=8只。

25、小张、小王二人同时从甲地出发，驾车匀速在甲乙两地之间往返行驶。小张的车速比小王快，两人出发后第一次和第二次相遇都在同一地点，问小张的车速是小王的几倍?_____
A: 1.5B: 2C: 2.5D: 3
参考答案: B 本题解释:【答案】B。2 解析：第一次相遇小张、小王二人的路程和为甲乙两地距离的2倍，从第一次相遇到第二次相遇，两人路程和仍为甲乙两地距离的2倍，即两次相遇所用时间相同。第一次相遇小王走的路程为x，相遇后小张需要走x到甲地，然后从甲地折返x回到同一地点相遇。所以相同时间内小张走的距离是小王的2倍，即车速是小王的2倍。

26、10个人欲分45个苹果，已知第一个人分了5个，最后一人分了3个，则中间的8人一定存在连续的两人至少分了多少个苹果？_____
A: 8B: 9C: 10D: 11
参考答案: C 本题解释:【答案】C。解析：中间的8人共分得苹果45－5－3＝37（个），将中间的8人分为4组，即（第2、3个人）（第4、5个人）（第6、7个人）（第8、9个人）。由37＝9×4+1可知，必有1组，即连续的两人分到了10个苹果。故答案为C。

27、某企业有甲、乙、丙三个仓库，且都在一条直线上，之间分别相距1千米、3千米，三个仓库里面分别存放货物5吨、4吨、2吨。如果把所有的货物集中到一个仓库，每吨货物每千米运费是90元，请问把货物放在哪个仓库最省钱?_____
A: 甲B: 乙C: 丙D: 甲或乙
参考答案: B 本题解释:B解析：此题遵循“小往大处靠”原则，先把2吨的货物移动到4吨那，这样就相当于有了6吨货物，然后在把5吨的货物也移动到6吨，综上所述，运到乙仓库最省钱。

28、Ａ、Ｂ两码头间河流长为 220 千米，甲、乙两船分别从 A、B 码头同时起航。如果相向而行5小时相遇，如果同向而行 55小时甲船追上乙船。则乙船在静水中每小时行驶多少千米？_____
A: 19B: 20C: 28D: 30
参考答案: B 本题解释:【答案】B。解析：甲乙相向而行时，不管哪个是上游，总是一个顺水、一个逆水。

29、某养殖场养了224头牧畜。其中羊比牛多38只,牛比猪多6只。如果将牛总数的75%用来换羊,一头牛换5只羊,那么,羊总共有多少只?_____
A: 342B: 174C: 240D: 268
参考答案: A 本题解释:【答案】A。解析:根据题意,设该养殖场原有羊x只、牛y只、猪z只,由题意得:x-y=38;y-z=6;x+y+z=224,解得x=102,y=64,那么用牛换羊后,羊总共有102+64×75%×5=342只。故选A。

30、某单位有宿舍11间，可以住67人，已知每间小宿舍住5人，中宿舍住7人，大宿舍住8人，则小宿舍间数是_____。
A: 6B: 7C: 8D: 9
参考答案: A 本题解释:【答案】A。解析：设小宿舍有x间，中宿舍有y间，大宿舍有11-x-y间。依题意5x+7y+8（11-x-y）=67，得到3x+y=21。〔化为标准形式〕因为x、y均是大于0的整数，所以x＜7。直接选A。〔确定解的范围〕

31、123456788×123456790-123456789×123456789=_____。
A: 0B: 1C: 2D: -1
参考答案: D 本题解释: D [解析] 原式=（123456789-1）×（123456789+1）-1234567892=1234567892-1-1234567892=-1故选D。

32、有关部门要连续审核30个科研课题方案，如果要求每天安排审核的课题个数互不相等且不为零，则审核完这些课题最多需要_____。
A: 7天B: 8天C: 9天D: 10天
参考答案: A 本题解释:【答案解析】1+2+3+4+5+6+7=28，再加一个2等于30，但因为是要互不相等，所以8天的情况和更多的情况都不符合，只能是7天，也就是1+2+3+4+5+6+9的情况，选A。

33、三件运动衣上的号码分别是1、2、3，甲、乙、丙三人各穿一件。现有25个小球。首先发给甲1个球，乙2个球，丙3个球。规定3人从余下的球中各取一次，其中穿1号衣的人取他手中球数的1倍，穿2号衣的人取他手中球数的3倍，穿3号衣的人取他手中球数的4倍，取走之后还剩下两个球。那么，甲穿的运动衣的号码是_____。
A: 1 B: 2 C: 3 D: 1或者2
参考答案: B 本题解释:B。【解析】首先发出了1+2+3=6个球，第二次又取出了25-6-2=17个球，穿2号和3号球衣的人第二次取走的球都是3的倍数，穿1号球衣第二次取走的球不多于3，所以只能是2个，即是乙。甲丙二人第二次共取走17-2=15个。若甲穿3号球衣，丙穿2号球衣，两人第二次只能取走3×3+1×4=13个，若甲穿2号球衣，丙穿3号球衣，两人第二次取走1×3+3×4=15个。甲穿的是2号球衣。

34、彼得定律是指每个组织都是由各种不同的职位、等级或阶层排列所组成的，每个人都隶属于其中的某个等级。在各种组织中，很多雇员都会因为业绩出色，而接受更高级别的挑战，被一直晋升，直到被晋升到一个他无法称职的位置，他的提升过程便终止了。根据上述定义，下列描述符合彼得定律的是_____。
A: 东南地区业务员杜拉多次蝉联公司销售冠军，很快就晋升为东南地区业务主管。上任后，杜拉雷厉风行制定新规则，引起了一些人的不满，杜拉费尽心思才安抚下来B: 张教授有许多重要的科研成果，而且深受学生喜爱，但是他被提拔为副校长之后，就再也没有出过一项重大科研成果了C: 足球教练马拉曾带领国家队多次在世界杯上取得好成绩，因此被任命为主管足球的官员。但是他上任后，媒体常批评他无所作为D: 李鸿原来是A省重点中学的特级教师，前不久被调任A市教委主任，而A省教育厅厅长正好是他的老同学，于是有些人私底下说李鸿是靠走关系才当上主任的
参考答案: C 本题解释:定义的关键信息是“晋升到一个他无法称职的位置”。A项，杜拉制定新规则，可能损害了一些人的利益，从而引起他们的不满，但这并不能作为杜拉不称职的表现，何况最后杜拉也把他们安抚了下来。B项，张教授被提拔为副校长，他的身份从教授、学者转向了管理者，科研已经不再是他的本职工作，因此“再也没有出过一项重大科研成果”并非不称职的表现。D项，“有些人私底下说”可能是出于嫉妒心理，并没有证据证明李鸿不能胜任教委主任一职。C项，马拉作为教练确实很优秀，但是当他晋升为体育官员之后，却经常被批评为无所作为，说明他只适合教练这个位置，并不适合成为官员，因而他是被晋升到了“一个他无法称职的位置”上，符合定义，选C。

35、一条环形赛道前半段为上坡，后半段为下坡，上坡和下坡的长度相等。两辆车同时从赛道起点出发同向行驶，其中A车上下坡时速相等，而8车上坡时速比A车慢20%，下坡时速比A车快20%。则在A车跑到第几圈时，两车再次齐头并进？_____
A: 22B: 23C: 24D: 25
参考答案: D 本题解释:假定A车速度为v，则B车上坡速度为0.8v，下坡速度为1.2v。由等距离平均速度公式可知B车完成一圈的平均速度为0.96v。则A车与B车跑一圈的平均速度之比为25：24，因此A车完成25圈时，两车同时回到起点。故选D。

36、在春运高峰时，某客运中心售票大厅站满等待买票的旅客，为保证售票大厅的旅客安全，大厅入口处旅客排队以等速度进入大厅按次序等待买票，买好票的旅客及时离开大厅。按照这种安排，如果开10个售票窗口，5小时可使大厅内所有旅客买到票;如果开12个售票窗口，3小时可使大厅内所有旅客买到票，假设每个窗口售票速度相同。由于售票大厅入口处旅客速度增加到原速度的1.5倍，为了在2小时内使大厅中所有旅客买到票，按这样的安排至少应开售票窗口数为_____个。
A: 15B: 16C: 18D: 19
参考答案: C 本题解释:C。设每个窗口的服务速度为x人/小时，大厅入口处旅客速度为y人/小时，大厅内乘客有s人。开10个售票窗口，5小时可使大厅内所有旅客买到票，说明s+5y=5×10x;开12个售票窗口，3小时可使大厅内所有旅客买到票，说明s+3y=3×12x;y=72，s=15x。大厅入口处旅客速度增加到原速度的1.5倍，即1.5y，要想在2小时内使大厅中所有旅客买到票，按这样的安排至少应开售票窗口数为t个，s+2×1.5y=2×tx，解得t=18。

37、甲乙两人参加射击比赛，规定每中一发记5分，脱靶一发倒扣3分，两人各打了10分子弹后，分数之和为52，甲比乙多得了16分，问甲中了多少发?_____
A: 9B: 8C: 7D: 6
参考答案: B 本题解释:【答案】B。解析：甲、乙分数之和为52，差为16，则甲为（52+16）÷2=34分，根据鸡兔同笼公式可得，甲中了（34+3×10）÷（5+3）=8发。

38、某超市用2500元购进一批鸡蛋，销售过程中损耗鸡蛋10千克。已知超市每千克鸡蛋的售价比进价高1元，全部售完后共赚440元，则共购进这批鸡蛋_____千克。
A: 460B: 500C: 590D: 610
参考答案: B 本题解释:【答案】B。解析：假定每千克鸡蛋的进价为x，而全部售完共赚440元，因此实际售出鸡蛋千克数为440＋10x千克，加上损耗的10千克，共计450＋10x千克。由题意：（450＋10x）x＝2500，解得x＝5。因此共购进鸡蛋为2500÷5＝500千克。故正确答案为B。老师点睛:总价为2500元，比能够被鸡蛋的千克数整除，仅B选项符合。

39、某车间从3月2日开始每天调入人，已知每人每天生产～件产品，该车间从月1日至3月21日共生产840个产品.该车间应有多少名工人? _____
A: 20B: 30C: 35D: 40
参考答案: B 本题解释:【答案】B。解析：从3月2日开始调入的每一个人生产的产品的个数正好组成以1为公差的等差数列20，19，18，……1，得调入的人生产的总产品数是：（20+1）×20÷2=210（个），所以原有工人生产的产品数=840-210=630（个），每人每天生产一个，所以工人数=630/21=30（个）。

40、小张数一篇文章的字数，二个二个一数最后剩一个，三个三个一数最后剩一个，四个四个一数最后剩一个，五个五个一数最后剩一个，六个六个一数最后剩一个，七个七个一数最后剩一个，则这篇文章共有多少字?_____
A: 501B: 457C: 421D: 365
参考答案: A 本题解释:答案：A【解析】甲=丙×（1+20%）×（1+20%）=144%丙，则甲比丙多44%。

41、一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的：_____
A: AB: BC: CD: D
参考答案: B 本题解释:答案：B.[解析]本题为几何类题目。因为正三角形和一个正六边形周长相等，又正三角形与正六边形的边的个数比为1︰2，所以其边长比为2︰1，正六边形可以分成6个小正三角形，边长为1的小正三角形面积：边长为2的小正三角形面积=1︰4。所以正六边形面积：正三角形的面积=1×6/4=1.5。所以选B。

42、下列关于日常生活的说法，不正确的是_____。
A: 将装有苏打的盒子敞口放在冰箱里可以除异味B: 医用消毒酒精的浓度为75%C: “坐井观天，所见甚小”是由于光沿直线传播D: 若电脑着火，即使关掉主机、拔下插头，也不可向电脑泼水
参考答案: A 本题解释:可以除异味的是小苏打碳酸氢钠;苏打是碳酸钠，A选项说法错误。医用酒精浓度有75%和95%，95%的酒精常用擦拭紫外线灯;75%的酒精常用消毒，故B项正确。“坐井观天，所见甚小”，因为光是沿直线传播的，光线以井为界线传播进来，井外的光线被挡住不能传播进来，故光线进入眼睛就有限，看见的事物就很小，故C项正确。若电脑着火，泼水后电脑的温度突然降下来，会使炽热的显像管爆裂。此外，电脑内仍有剩余电流，泼水可能引起触电，故D项正确。本题答案为A。

43、有6张卡片，分别写着数字1，2，5，6，8，9。现在从中取出3张卡片，并排放在一起，组成一个三位数。问可以组成多少个不同的偶数?_____
A: 144个B: 120个C: 60个D: 12个
参考答案: C 本题解释:

44、Ａ，Ｂ两村庄分别在一条公路L的两侧，A到L的距离|AC|为1公里，B到L的距离|BD|为2公里，C,D两处相距6公里，欲在公路某处建一个垃圾站，使得A,B两个村庄到此处处理垃圾都比较方便，应建在离C处多少公里_____
A: 2.75B: 3.25C: 2D: 3
参考答案: C 本题解释:答案： C 解析：连接AB，交公路L于点E，E点就是A、B两个村庄到此处处理垃圾都比较方便的地方，三角形ACE相似于三角形BDE，则AC⊥CE=BD⊥DE,而CE+DE=6,AC=1,BD=2,解得CE=2,故应建在离C处2公里。

45、四个学生做加法练习，任写一个六位数，然后把个位数字(不等于0)移到这个数的最左边产生一个新的六位数，最后把这个新六位数与原数相加，分别得到以下四个六位数。则哪个结果有可能正确? _____
A: 172536B: 568741C: 620708D: 845267
参考答案: C 本题解释:

46、一本100多页的书，被人撕掉了4张.剩下的页码总和为8037。则该书最多有多少页_____
A: 134B: 136C: 138D: 140
参考答案: A 本题解释:【答案】A。解析：撕掉四张纸的页码数之和是偶数，由剩下页码数是奇数可知总的页码数是奇数，排除B、D。若为C，则撕掉的页码数之和是138×（138+1）÷2—8037=1554>138×8，矛盾。A项符合题意。

47、某公交线路有15站，假设一辆公交车从起点站出发，从起点站后，每一站都会有到前方每一站下车的乘客各一名上车，那么在第九站和第十站之间，车上有_____人？
A: 48B: 54C: 56D: 60
参考答案: B 本题解释:【答案】B。解析：解析1：总站点数为M，求第N站和第N＋1之间车上的人数，有下述公式，车上的人数＝N×（M－N），可知所求人数为9×（15-9）＝9×6＝54，故选B。解析2：第一站点有14个人上车，没有人下车，第二个站点有13个人上，1个人下车，所以到第九站时候，前面上车人数为14，13，12，11，10，9，8，7，6，根据等差数列求和公式，一共有（14＋6）×9÷2=90人，下车的人数为1，2，3，4，5，6，7，8，一共有（1＋8）×8÷2＝36，则到第九站点后，车上人数等于一到第九站上车的人减去一到第九站下车的人数，即90-36=54，故选B选项。此题不用考虑过于复杂，起始站为第一站。

48、甲地到乙地，步行比骑车速度慢75%,骑车比公交慢50%，如果一个人坐公交从甲地到乙地共用1个半小时，问：骑车从甲地到乙地多长时间? _____
A: 10分钟B: 20 分钟C: 30分钟D: 40分钟
参考答案: B 本题解释:B。设骑车的速度为x公里/小时，则步行速度为0.25x公里/小时，公车的速度为2x公里/小时。设甲乙两地距离为L公里，则L/0.25x+L/2x=1.5，得到L/x=1/3小时=20分钟，则骑车从甲地到乙地需20分钟。

49、早上7点两组农民开始在麦田里收割麦子，其中甲组20人，乙组15人。8点半，甲组分出10人捆麦子;10点，甲组将本组所有已割的麦子捆好后，全部帮乙组捆麦子;如果乙组农民一直在割麦子，什么时候乙组所有已割的麦子能够捆好?(假设每个农民的工作效率相同)_____
A: 10:45B: 11:00C: 11:15D: 11:30
参考答案: B 本题解释:工程问题。采用赋值法，赋值每个农民割麦子的效率为1，由题意，甲组割麦子的总量为20×1.5+10×1.5=45，故每个农民捆麦子的效率为45÷1.5÷10=3;设从10点之后经过x小时，乙组的麦子全部捆好。故乙组割麦子的总量为15×（3+x），捆麦子总量为20×3×x，二者应该相等，解得x=1（小时）;故11:00时麦子可以全部捆好（最后一步可以采用代入排除）。

50、3点19分时，时钟上的时针与分针所构成的税角为几度？_____
A: 14度B: 14.5度C: 15度D: 15.5度
参考答案: B 本题解释:【解析】B。14. 5度。一圈是360度。分针跑60分钟是一圈，360/60=每分钟6度 时针跑12小时是一圈，360/（12*60）=0.5度每分钟 3点19分时候分针跑了6*19=114。时针0.5*199=99.5。

51、有5位田径运动员争夺3项比赛的冠军，若每项只设1名冠军，则获得冠军的情况可能有_____。
A: 124种B: 125种C: 130种D: 243种
参考答案: B 本题解释: B [解析] 每项比赛的冠军都有5种可能性，所以获得冠军的情况有C15×C15×C15=125（种）。故本题选B。

52、用两根同样长度的铁丝分别圈成圆形和正方形，圆形面积大约是正方形面积的几倍？_____
A: 3π B: 4/π C: 5π D: 6π
参考答案: B 本题解释: 【解析】B。设铁丝长度为X，则围成圆形的半径为X/2π，故面积为X2/4π，而其围成的正方形边长为x/4，则其面积为X2/16，所以圆形面积为正方形面积的4/π倍。

53、某次抽奖活动在三个箱子中均放有红、黄、一绿、蓝、紫、橙、白、黑8种颜色的球各一个，奖励规则如下：从三个箱子中分别摸出一个球，摸出的3个球均为红球的得一等奖，摸出的3个球中至少有一个绿球的得二等奖，摸出的3个球均为彩色球(黑、白除外)的得三等奖。问不中奖的概率是多少？_____
A: 在 0～25%之间B: 在25~50%之间C: 在50～75%之间D: 在75~100%之间
参考答案: C 本题解释:C。

54、在9×9的方格表中，每行每列都有小方格被染成黑色，且一共只有29个小方格为黑色。如果a表示至少包含5个黑色小方格的行的数目，b表示至少包含5个黑色小方格的列的数目，则a+b的 最大值是_____。
A: 25B: 10C: 6D: 14
参考答案: B 本题解释:B【解析】假设a+b≥11，且a≥b，则2a≥11，因为不存在染半格的情况，所以a≥6。那么这a行中至少有黑色小方格6×5=30（个），与题干中只有29个黑色小方格的条件相矛盾，因此假设不成立，a+b≤10，当a+b=10时，黑色小方格的分布如下图。故本题答案为B。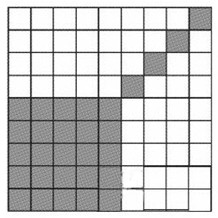

55、2011×201+201100—201.1×2910的值为_____。
A: 20110B: 21010C: 21100D: 21110
参考答案: A 本题解释:原式=2011×（201+100—291）=2011×10=20110。故选A。

56、在距离10千米的两城之间架设电线杆，若每隔50米立一个电线杆，则需要有_____个电线杆。
A: 15B: 201C: 100D: 250
参考答案: B 本题解释:B 【解析】所需数量为长度数除以间隔数加1。

57、某人同时购买2年期、5年期和10年期三种国债，投资额的比为5：3：2。后又以与前次相同的投资总额全部购买5年期国债，则此人两次对5年期国债的投资额占两次总投资的比例的_____。
A: 3/5B: 7/10C: 3/4D: 13/20
参考答案: D

58、123456788×123456790-123456789×123456789=_____。
A: 0B: 1C: 2D: -1
参考答案: D 本题解释: D [解析] 原式=（123456789-1）×（123456789+1）-1234567892=1234567892-1-1234567892=-1故选D。

59、某单位举行“庆祝建党90周年”知识抢答赛，总共50道抢答题。比赛规定：答对1题得3分，答错1题扣1分，不抢答得0分。小军在比赛中抢答了20道题，要使最后得分不少于50分，则小军至少要答对_____道题。
A: 16B: 17C: 18D: 19
参考答案: C 本题解释:假设答对2题，取最坏情形，剩下都答错，则答错20—x题，总分不少于50则有3x-（20-z）≥50，求得x≥17.5，取最小值为18。

60、已知一杯茶水有若干克，第一次加入一定量的水后，茶水的浓度为6%，第二次又加入同样多的水后，茶水的浓度为4%，求第三次加入同样多的水后茶水的浓度为多少?_____
A: 1%B: 2%C: 3%D: 3.5%
参考答案: C 本题解释:C【解析】设第一次加完水后，含茶6份，含水94份，这样茶水浓度就为6%，第二次加完水后，茶水总量为6÷4%=150份，所以第二次加水为150-100=50份，第三次加入的水也为50份，茶水浓度为6÷（150+50）=0.03=3%。所以，第三次加入同样多的水后茶水的浓度变为3%。故本题正确答案为C。

61、有面值为8分、1角和2角的三种纪念邮票若干张，总价值为1元2角2分，则邮票至少有_____。
A: 7张B: 8张C: 9张D: 10张
参考答案: C 本题解释:C【解析】要使邮票最少，则要尽量多的使用大面额邮票，所以要达到总价值，2角的邮票要使用4张，1角的邮票要使用1张，8分的邮票要4张，这样使总价值正好为1元2角2分，所以要用9张。

62、画一个边长为2cm的正方形，再以这个正方形的对角线为边画第二个正方形，再以第二个正方形的对角线为边画第三个正方形，则第三个正方形面积为_____平方厘米。
A: 32B: 16C: 8D: 4
参考答案: C 本题解释:C由题可知第2个正方形对角线长为2cm;则第三个正方形的面积为（2）2=8（平方厘米）;正确答案为C。

63、一个快钟每小时比标准时间快3分钟，一个慢钟每小时比标准时间慢2分钟。如果将两个钟同时调到标准时间，结果在24小时内，快钟显示11点整时，慢钟显示9点半。则此时的标准时间是_____。
A: 10点35分B: 10点10分C: 10点15分D: 10点06分
参考答案: D 本题解释:【答案】D。解析：应用比例，两个钟转动速度之差的比，即等于两钟钟面运行时长的差额之比。快钟与标准时间的之差、慢钟与标准时间的之差两者比为3：2，最终时间快钟、慢钟相差1.5小时，因此快钟与标准时间之差为1.5×3/5＝0.9小时，则标准时间为11（时）－60×0.9（分）=10（时）06（分）。故正确答案为D。

64、某医院有一氧气罐匀速漏气，该氧气罐充满后同时供40人吸氧，60分钟后氧气耗尽，再次充满该氧气罐同时供60个人吸氧，则45分钟后氧气耗尽。问如果该氧气罐充满后无人吸氧，氧气耗尽需要多长时间？_____
A: 1.5小时B: 2小时C: 2.5小时D: 3小时
参考答案: D 本题解释:【答案】D。解析：这是一个变形的牛吃草问题。设原有氧气为M，漏气速度为V，则可得（40＋V）×60＝（60＋V）×45＝M，解得V＝20，M＝3600，如果没人吸氧，则可得耗尽的时间为3600÷20＝180分钟，即3小时。故正确答案为D。

65、一群人坐车旅游，每辆车坐22人，剩5人没有座位，每辆坐26人，空出5个座位， 问每辆车坐25人，空出多少座位? _____
A: 20B: 15C: 10D: 5
参考答案: C 本题解释: C。一盈一亏型，车的数量为（15+5）÷ （26-22）=5,则共有5×22+5=115人。则坐25人时，115 ÷ 25=4……15，即需要5辆车，空出25-15=10个座位。

66、A、B、C、D四支球队开展篮球比赛，每两个队之间都要比赛1场，已知A队已比赛了3场，B队已比赛了2场，C队已比赛了1场，D队已比赛了几场？（）
A: 3B: 2C: 1
参考答案: B 本题解释:每个球队要比赛3场，则A队和B队、C队、D队各比赛1场，C队和A队比赛1场，B队和A队、D队各比赛1场，故D队比赛了2场。所以选B。

67、在一次考试中，赵、钱、孙三人的平均分是81分，钱、孙、李三人的平均分是74分，已知赵的分数是93分，那么李的分数是_____
A: 86分B: 75分C: 72分D: 68分
参考答案: C 本题解释:【解析】C。赵、钱、孙三人的总分是81×3=243(分)，钱、孙、李三人的总分是74×3=222(分)，那么243-222=21(分)就是赵的分数减去李的分数之差，已知赵的分数是93分，则李的分数为93-21=72(分)。

68、甲、乙两人骑车同时从家出发相向而行，甲每分钟行600米，乙每分钟行750米，在距两家中点600米的地方相遇。问两家相距多少米_____
A: 2150B: 1350C: 1200D: 10800
参考答案: D 本题解释:【解析】D。甲的速度比乙的速度慢，说明甲所行路程距离中点还有600米，而乙行走的路程超过中点600米，即相同的时间内乙比甲多走了600+600=1200(米)。由“追及时间=追及路程÷速度差”可以求出相遇时间：(分钟)，因此两家的距离是(米)。

69、出租车在开始10千米以内收费10.5元，以后每走1千米，收费1.7元。请问走25千米需收多少钱?_____
A: 20.6元　B: 35元　C: 36.5元D: 36元
参考答案: D 本题解释:D

70、对某单位的100名员工进行调查，结果发现他们喜欢看球赛和电影、戏剧。其中58人喜欢看球赛，38人喜欢看戏剧，52人喜欢看电影，既喜欢看球赛又喜欢看戏剧的有18人，既喜欢看电影又喜欢看戏剧的有16人，三种都喜欢看的有12人，则只喜欢看电影的有_____。
A: 22人B: 28人C: 30人D: 36人
参考答案: A 本题解释:【答案解析】本题可以使用阴影覆盖法，即100-(40+18+20)=22(人)，故远A项。

71、有一根长240米的绳子，从某一端开始每隔4米作一个记号，每隔6米也作一个记号。然后将标有记号的地方剪断，则绳子共剪成_____段。
A: 40B: 60C: 80D: 81
参考答案: C 本题解释:【答案】C。解析：容斥原理，每隔4米作一个记号，则作记号数为240÷4－1＝59；每隔6米作一个记号，则作记号数为240÷6－1＝39；其中每隔12米的记号重复被作两次，类似的记号数为240÷12－1＝19。因此做记号总数为59＋39－19＝79，即绳子被剪成80段。故正确答案为C。两集合容斥原理公式：|A∪B|＝|A|＋|B|－|A∩B|

72、有一工作，甲做2天后乙接着做，做了10天后完成了工作。已知乙单独完成需要30天，那么甲单独完成此工作需要_____天。
A: 3天B: 1天C: 10天D: 2天
参考答案: A 本题解释:【答案解析】由题可知，甲做2天，相当于乙做20天，则乙做30天的工作，甲3天即可完成。

73、甲、乙、丙三名运动员囊括了全部比赛项目的前三名，他们的总分分别是8、7和17分，甲得了一个第一名，已知各个比赛项目分数相同，且第一名的得分不低于二、三名得分的和，那么比赛共有多少个项目?_____
A: 3B: 4C: 5D: 6
参考答案: B 本题解释:【答案解析】全部比赛前三名的总分为8+7+17=32分，每个项目前三名的分数和至少是3+2+1=6分，所以每个项目前三名的分数和应该是32的大于6的约数，只能是8、16、32;如果是16或32，因为甲得了一个第一，所以甲的得分应大于8，不合题意，所以每个项目前三名的分数和是8分，共有项目32÷8=4个。

74、某商场出售甲乙两种不同价格的笔记本电脑，其中甲电脑连续两次提价10%，乙电脑连续两次降价10%，最后两种电脑均以9801元售出各一台，与价格不升不降比较，则商场盈亏情况是_____。
A: 不亏不赚B: 少赚598元C: 多赚980.1元D: 多赚490.05元
参考答案: B 本题解释:【答案】B。解析：由题干可知价格调整之前，乙电脑价格高于甲电脑，则乙电脑两次降价10%降的部分要大于甲电脑两次提价10%的部分，因此调整后两台电脑的总价格小于调价前的价格，从而商场少赚了，故正确答案为B。

75、一只油轮从甲港顺流而下到乙港，马上又逆水返回甲港，共用8小时，顺水每小时比逆水每小时多行12千米，前4小时比后4小时多行30千米，则甲、乙两港相距_____千米。
A: 72B: 60C: 55D: 48
参考答案: C 本题解释:【解析】由于顺水速度大于逆水速度。且顺水、逆水的行程相等，则顺水时间小于逆水时间，后4/小时全是逆水，前4小时先是顺水后是逆水，顺水时间=30÷12=2.5小时，逆水时间=8-2.5=5.5/小时，故顺水速度：逆水速度=5.5：2.5=11：5，顺水速度=12÷（11.-5）×11=22千米/时，两港距离=22×2.5=55（千米）。故选C。

76、小明和小方各走一段路，小明走的路程比小方多1/5，小方用的时间比小明多1/8。小明和小方的速度之比是多少?_____
A: 37∶14B: 27∶20C: 24∶9D: 21∶4
参考答案: B 本题解释: B【解析】依题意，小明与小芳路程的比是（1+1/5）：1=6：5小明与小芳时间的比是1：（1+1/8）=8：9小明与小芳速度的比是：6/8：5/9=27：20。

77、在一个口袋中有lO个黑球、6个白球、4个红球.至少从中取出多少个球才能保证其中有白球? _____
A: 14B: 15C: 17D: 18
参考答案: B

78、超市规定每3个空汽水瓶可以换一瓶汽水，小李有11个空汽水瓶，最多可以换几瓶汽水?_____
A: 5瓶.B: 4瓶C: 3瓶D: 2瓶
参考答案: A 本题解释:A【精析】11个空汽水瓶可以换3瓶汽水余2个空瓶，3瓶汽水喝完之后一共余5个空汽水瓶，向超市借1瓶汽水，喝空之后退回6个空瓶，即再换2瓶汽水。因此3+2=5。

79、一个边长为8的立方体，由若干个边长为l的立方体组成，现在要将大立方体表面涂漆，请问一共有多少个小立方体被涂上了颜色?_____
A: 296B: 324C: 328D: 384
参考答案: A

80、某区要从10位候选人中投票选举人大代表，现规定每位选举人必须从这10位中任选两位投票，问至少要有多少位选举人参加投票，才能保证有不少于10位选举人投了相同两位候选人的票?_____
A: 382位B: 406位C: 451位D: 516位
参考答案: B 本题解释:【答案】B。解析：从10位候选人中选2人共有种票，则每种票有9张相同时需要×9=405个人投票，那么只需要再加一人可以保证有不少于10人投了相同两位候选人的票。

81、A、B、C、D、E，5个小组开展扑克牌比赛，每两个小组之间都要比赛一场，到现在为止，A组已经比赛了4场，B组已经比赛了3场，C组已经比赛了2场，D组已经比赛了1场，问E组已经比赛了几场（）
A: oB: 1C: 2D: 3
参考答案: C 本题解释:C【解析】A组已经比赛了4场，说明A组与B、C、D、E这4个组都进行过比赛;D组已经比赛了1场，则根据上一个条件，D组只与A组进行过比赛;B组已经比赛了3场，则根据上一个条件，B组只与A、C、E组进行过比赛;C组已经比赛了2场，则根据上面的条件，C组只能与A、B组进行过比赛;所以E组与A、B组进行过比赛。

82、如果一个三角形的底边长增加10%，底边上的高缩短10%，那么这个新三角形的面积是原来三角形面积的_____。
A: 90%B: 80%C: 70%D: 99%
参考答案: D 本题解释:D解析：设原三角形底边为a，高为h，面积为S，则得：S=1/2ah。那么新三角形S新=1/2a(1+10%)?h(1-10%)=1/2?ah×99%=99%S，故答案为D。

83、甲、乙、丙三队在A、B两块地植树，A地要植树900棵，B地要植树1250棵，已知甲、乙、丙每天分别能植树24，30，32棵，甲在A地植树，丙在B地植树，乙先在A地植树，然后转到B地植树。两块地同时开始同时结束，乙应在开始后第几天从A地转到B地?_____
A: 5B: 7C: 9D: 11
参考答案: D 本题解释:D【解析】 植树共需（900+1250）÷（24+30+32）=25（天）。乙应在A地干（900-24×25）÷30=10（天），第11天转到B地。故本题正确答案为D。

84、一条公路旁有A、B、C、D、E5个货站。每两个货站之间的距离相等，现要将这5个货站集中到一个货站，已知A、B、C、D、E的货物分别为70吨、30吨、60吨、50吨、40吨，问应集中到哪一个货站可使运费最省? _____
A: AB: BC: CD: E
参考答案: C 本题解释:C。五个货站物资总数的一半为（70+30+60+50+40）÷2=125吨，因为A、E两站都小于125吨，所以都往中间靠一站，此时，B站：30+70=100吨，D站：50+40=90吨，B、D两站仍小于125吨，再往中间靠一站，集中到C站。因此集中到C站可使运费最省。

85、一个盒子里面装有10张奖券，只有三张奖券上有中奖标志，现在5人每人摸出一张奖券，至少有一人的中奖概率是多少? _____
A: 4/5 B: 7/10 C: 8/9 D: 11/12
参考答案: D 本题解释:D【解析】至少有一人中奖，那算反面就是没有人中1-（7/10）×（6/9） ×（5/8） ×（4/7） ×（3/6）=11/12。

86、从装满1000克浓度为50%的酒精瓶中倒出200克酒精，再倒入蒸馏水将瓶加满。这样反复三次后，瓶中的酒精浓度是多少?_____
A: 22.5%B: 24.4%C: 25.6%D: 27.5%
参考答案: C 本题解释: C 解析：每次操作后，酒精浓度变为原来的（1000-200）÷1000=0.8，故反复三次后浓度变为50%×0.8×0.8×0.8=25.6%。

87、两排蜂房，一只蜜蜂从左下角的1号蜂房到8号蜂房，假设只向右方(正右或右上或右下)爬行，则不同的走法有_____。
A: 16种B: 18种C: 21种D: 24种
参考答案: C 本题解释:

88、小张从家到单位有两条一样长的路.一条是平路、另一条是一半上坡路，一半下坡路，小张上班走这两条路所用的时间一样多。已知下坡的速度是平路的1.5倍，那么上坡的速度是平路的_____倍。
A: 3/5B: 2/5C: 1/4D: 3/4
参考答案: D 本题解释:【答案】D。解析：因为距离和时间都相同，则可以设路程是1，时间也是1，那么平路的速度为1÷1=1，又因为上坡和下坡路各一半也相同，那么上坡和下坡的路程都是O.5。下坡的速度为1.5，则下坡时问为0.5/1.5=1/3，因此上坡时间为1—1/3=2/3，上坡速度为1/2÷2/3=3/4。

89、已知29832983…298302能被18整除，那么n的最小值是_____。
A: 4B: 5C: 6D: 7
参考答案: A 本题解释:【解析】18=2×9，这个多位数的个位上是2，满足被2整除，因此，只需考虑个位数字之和能否被9整除的问题。（2+9+8+3）×n+0+2=22n+2是9的倍数，22×4+2=90=9×10，那么n的最小值为4。

90、已知2008被一些自然数去除，得到的余数都是10，那么，这些自然数共有_____。
A: 10B: 11C: 12D: 9
参考答案: B 本题解释:【答案解析】解析：余10=>说明2008-10=1998都能被这些数整除。同时，1998=2×3×3×3×37，所以，取1个数有37，2，3。---3个。，只取2个数乘积有3×37，2×37，3×3，2×3。---4个。，只取3个数乘积有3×3×37，2×3×37，3×3×3，2×3×3。---4个。只取4个数乘积有3×3×3×37，2×3×3×37，2×3×3×3。---3个。只取5个数乘积有2×3×3×3×37---1个。总共3+4+4+3+1=15，但根据余数小于除数的原理，余数为10，因此所有能除2008且余10的数，都应大于10=>2，3,3×3，2×3被排除。综上，总共有3+4+4+3+1-4=11个。

91、出租车队去机场接某会议的参会者，如果每车坐3名参会者，则需另外安排一辆大巴送走余下的50人;如每车坐4名参会者，则最后正好多出3辆空车。问该车队有多少辆出租车?_____
A: 50B: 55C: 60D: 62
参考答案: D 本题解释:方程问题。设有x辆出租车，由题意列方程：3x+50=4（x-3），解得x=62。

92、在1至100这100个数中，有既不能被5整除也不能被9整除的数，它们的和是_____。
A: 1644B: 1779C: 3406D: 3541
参考答案: D 本题解释:【答案解析】先求出被5或9整除的数的和。1至100中被5整除的数有5，10，15，…，100，和为5+10+15+…+100=(100+5)×20÷2=10501至100中被9整除的数有9，18，…，99，和为9+18+27+…+99=(9+99)×11÷2=594又因为1～100中，45，90这两个数同时被5与9整除，于是所求的和是(1+2+…+100)-(5+10+…+100)-(9+18+…+99)+(45+90)=3541。因此，本题正确答案为D。

93、某条道路的一侧种植了51棵梧桐树，其中道路两端各有一棵，且相邻两棵树之间的距离相等。如果需要在这一侧再多种10棵树，且通过移动一部分树(不含首尾两棵)使所有相邻两棵树之间的距离仍然相等，则这51棵树中至少有多少棵不需要移动位置？_____
A: 9B: 10C: 11D: 12
参考答案: C 本题解释:【答案】C。解析：设路长为50×60米，则第一次的间距为60米，第二次的间距为50米，不需要移动位置的树距起点的距离必须为60和50的公倍数，即距离应是300的倍数。总长为3000米，则中间有9棵树不需要移动，再加上首尾两棵，一共有11棵树不需要移动。因此，本题选择C选项。

94、某S为自然数，被10除余数是9，被9除余数是8，被8除余数是7，已知100＜S＜1000，请问这样的数有几个？_____
A: 5 B: 4 　C: 3 　D: 2
参考答案: D 本题解释:D。【解析】被N除余数是N-1，所以这个数字就是几个N的公倍数-1。10，9，8的公倍数为360n（n为自然数），因为100＜S＜1000，所以有两个数符合条件。

95、甲以每小时6千米的速度步行从A地前往B地，在甲出发90分钟时，乙发现甲落下了重要物品，立即骑自行车以每小进12千米的速度追甲，终于在上午11点追上了甲。问甲出发时间是上午几点？ _____
A: 7 B: 8 C: 9 D: 10
参考答案: B 本题解释:B。追及路程为6×1.5＝9千米，甲乙速差为12－6＝6千米/小时，则乙追上甲需要9÷6＝1.5小时。因此甲出发时间是早上8点。故选B项。

96、小新做一道加法题，由于粗心将一个加数万位上的3看成8，百位上的1看成7，个位上的9看成6，算得的结果是95050。则这道加法题的正确答案本应是_____。
A: 44447B: 45453C: 44453D: 45405
参考答案: C 本题解释:C【解析】本题只要找出错看的加数和本来的加数之间的差值，用错误结果加上少加的数，减去多加的数，即可得出正确结果。即正确答案=95050-（80000-30000）-（700-100）+（9-6）=95050-50000-600+3=44453由此可知本题正确答案为C。

97、某机关共有干部、职工350人，其中55岁以上共有70人。现拟进行机构改革，总体规模压缩为180人，并规定55岁以上的人裁减比例为70％。请问55岁以下的人裁减比例约是多少?_____。
A: 51％ B: 43％ C: 40％ D: 34%
参考答案: B

98、有三个居委会的居民共订600份《华西都市报》，每个居委会至少订199份，最多订201份，则不同的订报方式有_____种。
A: 3B: 5C: 6D: 7
参考答案: D 本题解释:【答案】D。解析：三个居委会分别订200、200、200和199、200、201两种情况，前一种方法数为1，后一种方法数为3×2×1＝6，1＋6＝7，故正确答案为D。

99、某论坛邀请了六位嘉宾，安排其中三人进行单独演讲，另三人参加圆桌对话节目。如每位嘉宾都可以参加演讲或圆桌对话，演讲顺序分先后且圆桌对话必须安排在任意两场演讲之间，问一共有多少种不同的安排方式？_____
A: 120 B: 240 C: 480 D: 1440
参考答案: B 本题解释:【解析】B。排列组合。240；先从六个人中选三个参加演讲，这三个全排列，再插孔法放入两个对话节目。

100、一件工作甲先做6小时，乙接着做12小时可以完成。甲先做8小时，乙接着做6小时也可以完成。如果甲先做3小时后，再由乙接着做，还需要多少小时完成? _____
A: 16B: 18C: 21D: 24
参考答案: C 本题解释:C【解析】设甲、乙两人每小时的工作量x、y，可列方程6x+12y=18x+6y=1 解得x=110y=130，甲先做了110×3，工作还剩1-310=710，故乙还需要710÷130=21 小时。故选C。