1、甲、乙、丙、丁和小强五位同学一起比赛象棋，每2人都要比赛1盘，到现在为止，甲已经赛了4盘，乙已经赛了3盘，丙赛了2盘，丁赛了1盘。问小强赛了几盘?_____ B: 4C: 2D: 5
参考答案: C 本题解释:参考答案:C题目详解: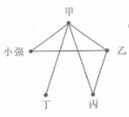五位同学的比赛关系如上图所示：甲已经赛了4盘可知：甲和所有人都比赛过;根据丁赛了1盘可知：丁只和甲比赛了一场;根据乙已经赛了3盘可知：乙与甲、丙、小强各比赛了一场;根据丙赛了2盘可知：丙和甲、乙各比赛了一场;故小强和甲、乙各比赛了一场。所以，选C。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛

2、(2008江西，第43题) 5个小组开展扑克牌比赛，每两个小组间都要比赛一场，到现在为止， 组已经比赛了4场， 组已经比赛了3场， 组已经比赛了2场， 组已经比赛了1场，问 组比赛了几场?_____ B: 1C: 2D: 3
参考答案: C 本题解释:参考答案:C题目详解:如图所示：比赛过的两支球队间用实线连接;未赛过的两支球队用虚线连接;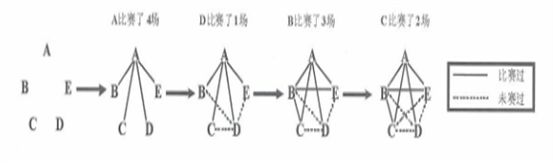根据上图：“组已经比赛了4场”可知：A和B，C，D，E都各自赛过一场;“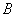组已经比赛了3场”和“D赛了一场”可知：B和A，C，E各自赛过一场;“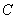组已经比赛了2场”可知：C和A，B赛过，从上可知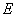：队参加了2场比赛。所以，选C。考查点:数量关系>来源:91考试网 91Exam.org;数学运算>排列组合问题>比赛问题>循环赛

3、西南赛区四支球队为了争夺小组第一名而进行小组循环赛，已知小马队已比赛了3场，小熊队已比赛了2场，小龙队已比赛了1场，问小牛队比赛了几场_____
A: 3B: 2C: 1
参考答案: B 本题解释:参考答案:B题目详解:小马队已比赛了3场：说明小马队和小熊队、小龙队、小牛队各打了1场;小龙队已比赛了1场：说明小龙队只和小马队比赛了1场;小熊队已比赛了2场：因为和小马队比赛了1场，所以还有1场比赛。因为小龙队只和小马队比赛过，所以小熊队只能和小牛队进行比赛。因此小牛队比赛了2场，分别是和小马队、小熊队进行的比赛。所以，选B。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛

4、8个甲级队应邀参加比赛，先平均分成两组，分别进行单循环赛，每组决出前两名，再由每组的第一名.另一组的第二名进行淘汰赛，获胜者角逐冠、亚军，败者角逐第3、4名，整个赛程的比赛场数是_____。
A: 16B: 15C: 14D: 13
参考答案: A 本题解释:参考答案:A题目详解:第一步进行单循环赛：8个队分成两组，每组四个队，进行单循环赛，共有场;第二步进行淘汰赛：共有4个队进入淘汰，需要比4场;一共是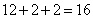：场;所以，选A。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛

5、有101位乒乓球运动员在进行冠军争夺赛。通过比赛，将从中产生一名冠军。这次比赛实行捉对淘汰制。在一轮比赛全部结束后，失败者失去继续比赛的资格，而胜利者再次抽签，参加下一轮的比赛。问一共要进行多少场比赛，才能最终产生冠军?_____
A: 32B: 63C: 100D: 101
参考答案: C 本题解释:参考答案:C题目详解:依题意：其实可以看成是一场比赛淘汰一个人;要得出冠军就要淘汰掉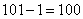个人;淘汰100个人即要进行100场比赛;所以，选C。考查点:数量关系>数学运算>排列组合问题>比赛问题>淘汰赛

6、小赵，小钱，小孙一起打羽毛球，每局两人比赛，另一人休息，三人约定每一局的输方下一局休息，结束时算了一下，小赵休息了2局，小钱共打了8局，小孙共打了5局，则参加第9局比赛的是：_____
A: 小钱和小孙B: 小赵和小钱C: 小赵和小孙D: 以上皆有可能
参考答案: B 本题解释:参考答案:B题目详解:小赵休息的2局即是小钱和小孙打了2局：则小钱和小赵打了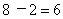局;小孙和小赵打了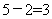局：则一共打了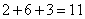局;所以小孙11局中休息了6打了5局;由于不可能连续休息2局，所以小孙一定是休息1局打1局……;所以第9局小孙休息;小赵和小钱打;所以，选B。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛

7、(2009天津、湖北、陕西联考，第95题)有4支队伍进行4项体育比赛，每项比赛的第一、第二、第三、第四名分别得到5，3，2，1分，每队的4项比赛的得分之和算作总分，如果已知各队的总分不相同，并且A队获得了三项比赛的第一名，问总分最少的队伍最多得多少分?_____
A: 7B: 8C: 9D: 10
参考答案: B 本题解释:参考答案:B题目详解:本题需要运用“构造法”和“极端法”。由于题目求“总分最少的队伍最多得多少分”，我们需要让各队的得分尽可能的平均。每项比赛产生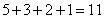分，4项比赛一共产生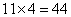分，最终平均每人得到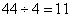分。A已经获得了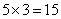分，超过平均分，需要A最后=场比赛得尽量少的分，即1分，那么剩下3个人将得到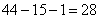分。要让剩下三个人比分尽可能的平均，可以构造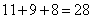，在这个条件下，部分最少的队伍可以得到最多的分数，即8分。下面我们构造这种比赛的情形：考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛

8、某区中学生足球联赛共赛8轮(每队均需赛8场)。规则是：胜一场得3分;平一场得1分;负一场得0分。在这次联赛中，A队踢平场数是所负场的2倍，共得17分。问该队胜了几场?_____
A: 2B: 3C: 4D: 5
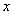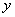参考答案: D 本题解释:参考答案题目详解:设胜了场，负了场: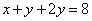;;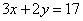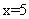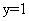，;胜了5场;所以，选D。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛

9、有8个队参加比赛，采用所示的淘汰制方式。问在比赛前抽签时，可以得到多少种实质不同的比赛安排表?_____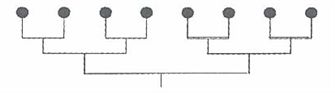
A: 4030B: 315C: 5040D: 164
参考答案: B 本题解释:参考答案:B题目详解:我们标上字母如图:全排列为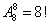。因为A/B，B/A实质赛程一样;同理：C/D，E/F，G/H，I/J，K/L，M/N均是，所以除以7个2。于是，共有种实质不同的赛程安排。所以，选B。考查点:数量关系>数学运算>排列组合问题>比赛问题>淘汰赛

10、16支球队分两组，每组打单循环赛，共需打_____场比赛。
A: 16B: 56C: 64D: 120
参考答案: B 本题解释:参考答案:B题目详解:依题意：16支球队分两组，每组8支队;每个队都要跟其余7个球队赛一场：因此，每组需要打8×7÷2=28场比赛，两组一共是28×2=56场比赛。所以，选B。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛