1、将棱长为1的正方体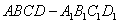 ,切去一角
,切去一角 后,剩下几何体的表面积是_____。
后,剩下几何体的表面积是_____。
A: 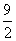 B: 5C:
B: 5C: 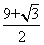 D:
D: 
参考答案: C 本题解释:参考答案:C题目详解:如右图所示,可知:原正方体表面积: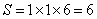 ;减少的表面积为:
;减少的表面积为: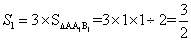 ;增加的表面积为:
;增加的表面积为: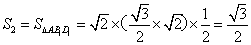 ;故剩下面积为:
;故剩下面积为: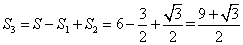 。所以,选C。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选C。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
2、(2005上海)棱长为a的正方体 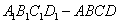 中,求
中,求 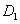 到面
到面 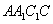 的距离_____。
的距离_____。 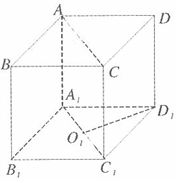
A: 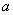 B:
B: 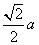 C:
C: 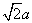 D:
D: 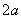
参考答案: B 本题解释:参考答案:B题目详解:根据题意,连接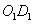 (
( 是
是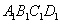 的中心),∵在正方体
的中心),∵在正方体 ,
,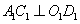 ,
,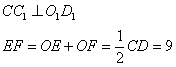 ,且
,且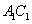 与
与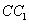 相交与点
相交与点 .∴
.∴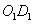
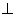 面
面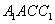 ,∴
,∴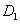 到面
到面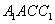 的距离就是求
的距离就是求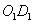 ,则:
,则: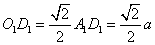 ,所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
,所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
3、(2009江苏)如下图,将一个表面积为36平方米的正方体等分成两个长方体,再将这两个长方体拼成一个大长方体,则大长方体的表面积是_____。 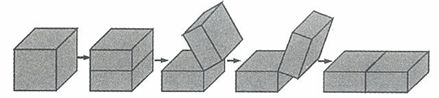
A: 24平方米B: 30平方米C: 36平方米D: 42平方米
参考答案: D 本题解释:参考答案 题目详解:解法一:已知原来正方体每个面的面积都是6平方米,这个过程中,先产生了一个截面,新增了两个平面的面积,即增加了12平方米;原来在右边的那个面在接触过程中被遮住了,不再是表面,即减少了一个平面的面积,即减少了6平方米。综上,大长方体的表面积为
题目详解:解法一:已知原来正方体每个面的面积都是6平方米,这个过程中,先产生了一个截面,新增了两个平面的面积,即增加了12平方米;原来在右边的那个面在接触过程中被遮住了,不再是表面,即减少了一个平面的面积,即减少了6平方米。综上,大长方体的表面积为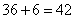 平方米。所以,选D。解法二:同样体积的图形当中,越接近于球,表面积越小,所以正方体变成长方体之后,表面积肯定会增加,由此可以直接判断D为正确答案。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
平方米。所以,选D。解法二:同样体积的图形当中,越接近于球,表面积越小,所以正方体变成长方体之后,表面积肯定会增加,由此可以直接判断D为正确答案。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
4、在一个长16米、宽12米、高8米的库房中最多可以装下多少只长4市尺、宽3市尺、高2市尺的箱子?_____
A: 1564B: 1728C: 1686D: 1835
参考答案: B 本题解释:参考答案:B题目详解:根据公式1米=3市尺先进行单位换算,库房的体积为: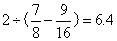 能放箱子的个数为:
能放箱子的个数为: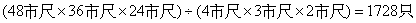 。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
5、一个长方形铁锭,底面周长为32厘米,长与宽的比是 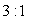 ,高比宽短
,高比宽短 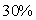 。用它刚好可以铸成高为6厘米的圆锥体,那么圆锥体的底面积为_____平方厘米。
。用它刚好可以铸成高为6厘米的圆锥体,那么圆锥体的底面积为_____平方厘米。
A: 67.2B: 201.6C: 537.6D: 1612.8
参考答案: A 本题解释:参考答案:A题目详解:先求出长方体的长、宽、高,长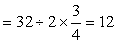 (厘米);宽
(厘米);宽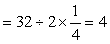 (厘米);高
(厘米);高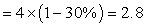 (厘米)。圆锥体的体积
(厘米)。圆锥体的体积 ,设圆锥体底面积为
,设圆锥体底面积为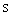 ,可得出:
,可得出: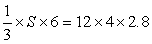 ,解得,
,解得,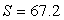 (平方厘米)。所以,选A。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
(平方厘米)。所以,选A。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
6、(2002浙江)如图所示,直线SA垂直于正方形ABCD,AC与BD相交于O,AB=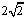 cm,SC=5cm,则点S到直线BC的距离是_____。
cm,SC=5cm,则点S到直线BC的距离是_____。 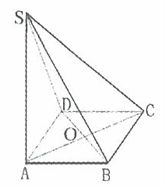
A: 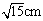 B:
B: 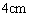 C:
C: 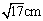 D:
D: 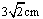
参考答案: C 本题解释:参考答案:C题目详解:根据三垂线定理,在上图中,SA垂直于正方形ABCD,AB⊥BC,则CB⊥BC所以,题目所求的点S到直线BC的距离是SB,再根据勾股定理,可知: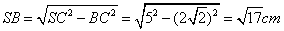 。所以,选C。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
。所以,选C。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
7、用一个平面将一个边长为1的正四面体切分为两个完全相同的部分,则切面的最大面积为:_____
A: 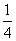 B:
B: 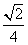 C:
C: 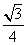 D:
D: 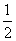
参考答案: B 本题解释:参考答案:B题目详解:正四面体是正三棱锥,过一条侧棱及其所对侧面的高作切面即可将正四面体切分为两个完全相同的部分,且切面的面积最大,如图中的 。四个面都是边长为1的等边三角形,底面的高
。四个面都是边长为1的等边三角形,底面的高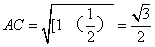 ;O是底面的中心,
;O是底面的中心,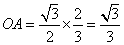 ;四面体的高,也就是
;四面体的高,也就是 的高:
的高: ;所以,切面的最大面积为
;所以,切面的最大面积为 。所以,选B。
。所以,选B。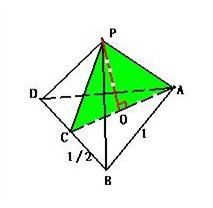 考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
8、(2004国家,A类,第42题)一个边长为8的立方体,由若干个边长为l的立方体组成,现在要将大立方体表面涂漆,请问一共有多少个小立方体被涂上了颜色?_____
A: 296B: 324C: 328D: 384
参考答案: A 本题解释:参考答案:A题目详解:本题欲求出有多少个小立方体被涂上颜色,可先求出有多少个小立方体没有被染色。没有被染色的小立方体构成一个较小的立方体,体积为: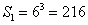 。大立方体的体积为:
。大立方体的体积为: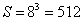 ;所以染了色的总体积=大立方体体积—小立方体体积=
;所以染了色的总体积=大立方体体积—小立方体体积=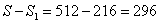 ,而每个小立方体的体积为1,所以有296÷1=296个小立方体被涂上了颜色。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
,而每个小立方体的体积为1,所以有296÷1=296个小立方体被涂上了颜色。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
9、正方体 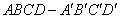 中,侧面对角线
中,侧面对角线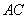 与
与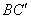 所成的角等于_____。
所成的角等于_____。 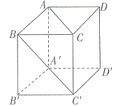
A: 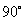 B:
B: 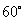 C:
C: 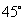 D:
D: 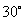
参考答案: B 本题解释:参考答案:B题目详解:根据题意,连接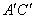 与
与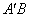 。∵
。∵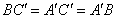 ∴
∴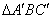 为等边三角形,又∵
为等边三角形,又∵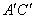 与
与 平行,∴侧面对角线
平行,∴侧面对角线 与
与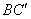 所成的角等于
所成的角等于 。因此,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
。因此,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
10、一个长方体的长、宽、高恰好是三个连续自然数,并且它的体积数值等于它的所有棱长之和的2倍,那么这个长方体的表面积为多少?_____
A: 74B: 148C: 150D: 154
参考答案: B 本题解释:参考答案:B题目详解:假设长方体的长、宽、高分别是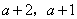 ,
,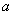 ,则:体积数值为:
,则:体积数值为: ,棱长之和的2倍为:
,棱长之和的2倍为: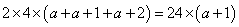 ,联立有:
,联立有: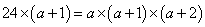 ,解得
,解得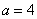 即长方体的长、宽、高分别为6,5,4,可见长方体的表面积为:
即长方体的长、宽、高分别为6,5,4,可见长方体的表面积为: 。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
11、(2003国家)一个长方体形状的盒子长、宽、高分别为20厘米、8厘米和2厘米,现在要用一张纸将其六个面完全包裹起来,要求从纸上剪下的部分不得用作贴补,请问这张纸的大小可能是下列哪一个?_____
A: 长25厘米、宽17厘米B: 长26厘米、宽14厘米C: 长24厘米、宽21厘米D: 长24厘米、宽14厘米
参考答案: C 本题解释:参考答案:C题目详解:长方体的表面积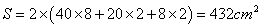 ;选项A中纸的面积
;选项A中纸的面积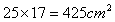 ;选项B中纸的面积
;选项B中纸的面积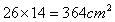 ;选项C中纸的面积
;选项C中纸的面积 ;选项D中纸的面积
;选项D中纸的面积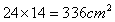 。纸的面积应该大于长方体的表面积,结合选项,选择C。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。纸的面积应该大于长方体的表面积,结合选项,选择C。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
12、把一个长18米、宽6米、高4米的大教室,用厚度为25厘米的隔墙将长分为3段,形成3个活动室(隔墙砌到顶),每间活动室的门窗面积都是15平方米,现在用石灰粉刷3个活动室的内墙壁和天花板,平均每平方米用石灰0.2千克,那么,一共需要石灰_____千克。
A: 68.8B: 74.2C: 83.7D: 59.6
参考答案: A 本题解释:参考答案:A题目详解:根据题意,可知:天花板总面积是:(18-0.25×2)×6=105平方米,内壁总面积是:(18-0.25×2)×4×2+4×6×6-15×3=239平方米,需用石灰粉刷的总面积是:105+239=344平方米,需用石灰为:344×0.2=68.8千克。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
13、有高度相等的A、B两个圆柱形容器,内口半径分别为6厘米和8厘米。容器A中装满水,容器B是空的,把容器A中的水全部倒入容器B中,测得容器B中的水深比容器高的 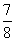 还低2厘米。容器的高度是多少厘米?_____
还低2厘米。容器的高度是多少厘米?_____
A: 5.6B: 6.4C: 8D: 9.6
参考答案: B 本题解释:参考答案:B题目详解:解法一:设容器高x厘米,那么A的容积就是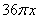 (立方厘米)。而容器B的底面积为
(立方厘米)。而容器B的底面积为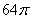 (平方厘米)。那么B中的水深是
(平方厘米)。那么B中的水深是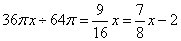 ,解得,
,解得,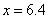 (厘米)。所以,选B。解法二:我们知道高相等的圆柱,底面积之比等于体积之比,同样体积相等的圆柱,底面积之比就是高之比。内半径为6厘米的圆柱的底面积是36π,内半径为8厘米的圆柱的底面积是64π,它们的比为9:16。这样我们就知道了,a容器中装满水倒入b容器中只能倒b容器的
(厘米)。所以,选B。解法二:我们知道高相等的圆柱,底面积之比等于体积之比,同样体积相等的圆柱,底面积之比就是高之比。内半径为6厘米的圆柱的底面积是36π,内半径为8厘米的圆柱的底面积是64π,它们的比为9:16。这样我们就知道了,a容器中装满水倒入b容器中只能倒b容器的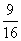 ,而b容器高的
,而b容器高的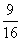 比
比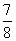 小2厘米,这样就转化成简单的分数除法应用题了。
小2厘米,这样就转化成简单的分数除法应用题了。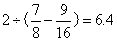 厘米。所以ab容器高6.4厘米。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
厘米。所以ab容器高6.4厘米。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
14、一个球体的半径增加10%后,它的表面积增长百分之几?_____
A: l0%B: 21%C: 33.1%D: 22%
参考答案: B 本题解释:参考答案:B题目详解:根据题意,可知:球体的表面积计算公式为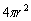 ,故半径增加10%后,表面积增加:
,故半径增加10%后,表面积增加: 。所以它的表面积增长了21%。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以它的表面积增长了21%。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
15、正四面体的棱长增长10%,则表面积增加_____
A: 21%B: 15%C: 44%D: 40%
参考答案: A 本题解释:参考答案:A题目详解:根据题意,可知:正四面体就是四个相等的正三角形。设原棱长a为1,则:原表面积为: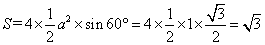 ;现表面积为:
;现表面积为: ;所以
;所以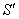 比S增加了:
比S增加了: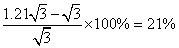 。所以,选A。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选A。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题