1、某年级有四个班级，不算一班有210人，不算二班有199人，不算三班有196人，不算四班有205人，问：这个年级共有_____人?
A: 240B: 270C: 320D: 3 60
参考答案: B 本题解释:B【解析】设一、二、三、四班的人数分别为a，b，c，d人。不算一班的人数是210人，即b+c+d=210;不算二班的人数是199人，即a+c+d=199;不算三班的人数是196人，即a+b+d=196;不算四班的人数为205人，即a+b+c=205;四个式子相加：3（a+k+c+d）=810。a+b+c+d=270，即这个年级共有270人，故应选B。

2、一个袋子里装有三种不同颜色但大小相同的小球。红色小球上标有数字1，黄色小球上标有数字2，蓝色小球上标有数字3。小明从袋中摸出10个小球，它们的数字和是21，那么小明摸出的小球中最多可能有多少个小球是红色的?_____
A: 3个B: 4个C: 5个D: 6个
参考答案: B 本题解释:【解析】设摸出的10个球中，红色小球有a个，黄色小球b个，那么蓝色小球有（10-a-b）个。根据题干可得:a+2b+3×（10-a-b）=21。整理得b=9-2a，显然a最大为4。这时b=1，则蓝色小球有10-1-4=5（个）。故本题正确答案为B。

3、某月刊杂志，定价2.5元，劳资处一些人订全年，其余人订半年，共需510元，如果订全年的改订半年，订半年的改订全年，共需300元，劳资处共多少人？_____
A: 20B: 19C: 18 D: 17
参考答案: C 本题解释: 【解析】本题用解方程的方法也可以解答，但是速度较慢。由题意可知，如果劳资处所有人都订一年半的话，总计810元;而单人订一年半的月刊需元;所以共有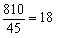人。故选C。

4、一个边长为8的正立方体，由若干个边长为1的正立方体组成，现在要将大立方体表面涂漆，问一共有多少小立方体被涂上了颜色？_____
A: 296 B: 324 C: 328 D: 384
参考答案: A 本题解释:A【解析】思路一：其实不管如何出，公式就是=>边长（大正方形的边长）3-（边长（大正方形的边长）-2） 3 。思路二：一个面64个，总共6个面，64×6=384个，八个角上的正方体特殊，多算了2×8=16个，其它边上的，多算了6×4×2+4×6=72，所以384-16-72=296。

5、有一个上世纪80年代出生的人，如果他能活到80岁，那么有一年他的年龄的平方数正好等于那一年的年份。问此人生于哪一年_____
A: 1980年 B: 1983年 C: 1986年 D: 1989年
参考答案: A 本题解释:【解析】A。1980～2069中只有一个平方数2025（即），由“有一年他的年龄的平方数正好等于那一年的年份”可知满足条件的那一年是2025年，此时他的年龄为45岁，因此此人生于2025-45=1980（年），符合“上世纪80年代出生”这个要求。

6、用2，3，4，5，6，7六个数字组成两个三位数，每个数字只用一次，这两个三位数的差最小是多少？_____
A: 47B: 49C: 69D: 111
参考答案: A 本题解释:因为每个数字只能用一次，显然首位决定大小，因此三个三位数的百位数字至少相差1，在这种情况下要使差值最小，则两个三位数为最接近，从而可知较小的三位数之末两位应尽可能大，而较大的三位数之末两位应尽可能小。在这个思想下，可知合适的三位数情况构造为523，476，此时三位数之末两位的差距最大，从而差值最小，最小差值为47。故选A。

7、某旅游景点商场销售可乐，每买3瓶可凭空瓶获赠1瓶可口可乐，某旅游团购买19瓶，结果每人都喝到了一瓶可乐，该旅游团有多少人?_____
A: 19B: 24C: 27D: 28
参考答案: D 本题解释: D 解析：由题意知：买2瓶可乐就可以喝3瓶，所以19：N=2：3，N=28.5，商家不可能亏本，所以取28，选D。

8、423×187-423×24-423×63的值是_____。
A: 41877B: 42300C: 42323D: 42703
参考答案: B 本题解释: B 【解析】原式可化为423×（187-24-63）。

9、地球表面的陆地面积和海洋面积之比是29︰71，其中陆地的四分之三在北半球，那么南、北半球海洋面积之比是_____
A: 284︰29B: 113︰55C: 371︰313D: 171︰113
参考答案: D 本题解释:【解析】D。根据题干中的比例关系，可以推断出南、北半球的海洋面积之比为：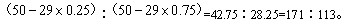

10、甲、乙、丙、丁四个人比赛打羽毛球，每两个都要赛一场，已知甲胜了丁，并且甲、乙、丙三人胜的场数相同，那么丁胜了几场？_____
A: 6 B: 0 C: 12 D: 3
参考答案: B 本题解释:【解析】B。每人至多赛3场，排除A、C。甲胜丁，则丁至少输1场，排除D。

11、某人同时购买2年期、5年期和10年期三种国债，投资额的比为5：3：2。后又以与前次相同的投资总额全部购买5年期国债，则此人两次对5年期国债的投资额占两次总投资的比例的_____。
A: 3/5B: 7/10C: 3/4D: 13/20
参考答案: D

12、新年晚会上，老师让每位同学从一个装有许多玻璃球的口袋中摸两个球，这些球给人的手感相同，只有红、黄、白、蓝、绿五色之分，结果发现总有两个人取的球颜色相同。由此可知，参加取球的至少有_____人。
A: 13B: 14C: 15D: 16
参考答案: D 本题解释:【解析】摸出两个球，两球的颜色不同的情况有C25=10种，两个球的颜色相同的情况有5种，共有15种情况，所以至少有16人。

13、有一笔奖金，按1：2：3的比例来分，已知第三人分450元，那么这笔奖金总共是_____元。
A: 1150 B: 1000 C: 900 D: 750
参考答案: C 本题解释:C。根据题意可知，这笔奖金共分为6份，而分到3份的第三人拿到了450元，则6份当是450×2=900元。所以正确答案为C项。

14、甲、乙、丙、丁四人今年分别是16、12、11、9岁。问多少年前，甲、乙的年龄和是丙、丁年龄和的2倍?_____
A: 4B: 6C: 8D: 12
参考答案: B 本题解释: 【解析】B。解法一、设x年前满足条件，则（16-x）+（12-x）=[（11-x）+（9-x）]×2;解法二、两组年龄差为8岁（分别作差5+3=8），当第一组为第二组两倍时肯定是16与8岁。现在第一组和为28岁，需要倒退12岁到16岁，需要6年，因为两个人一年一共倒退2岁。

15、某人做两位数乘两位数乘法时，把一个乘数的个位数5误写成3，得出的乘积是552，另一个学生却把5误写成8，得出的乘积是672，则正确的乘积是_____。
A: 585B: 590C: 595D: 600
参考答案: D 本题解释:【解析】（672-552）÷（8-3）=24，即另一个乘数是24;552÷24=23，故正确的乘数是25，则正确的乘积就是24×25=600。故选D。

16、一只猎豹锁定了距离自己200米远的一只羚羊，以108千米/小时的速度发起进攻，2秒钟后，羚羊意识到危险，以72千米/小时的速度快速逃命。问猎豹捕捉到羚羊时，羚羊跑了多少路程？_____
A: 520米 B: 360米 C: 280米 D: 240米
参考答案: C 本题解释:【答案】C。解析：108千米/小时=30米/秒，72千米/小时=20米/秒，开始猎豹距离羚羊200米，羚羊意识到危险的时候，猎豹距离羚羊200米-30米/秒×2秒=140米。根据追击问题计算公式：速度差×追击时间=路程差，即（30-20）t=140，t=14秒，即猎豹捕捉到羚羊时，羚羊跑了14秒，路程为20×14=280米。

17、有水果糖、奶糖、巧克力三袋重量不同的糖果，水果糖与奶糖的重量比是6：5，若水果糖的2/3被吃掉，且被吃掉的水果糖与被吃掉的巧克力的重量之比是5：4，那么这两种糖剩下的部分重量相等。问原先水果糖、奶糖、巧克力的重量之比是多少？_____
A: 35：30：31B: 25：20：21C: 30：25：26D: 42：35：40
参考答案: C 本题解释:C。

18、某单位有员工540人，如果男员工增加30人就是女员工人数的2倍，那么原来男员工比女员工多几人_____
A: 13B: 31C: 160D: 27
参考答案: C 本题解释:【答案】C。解析：设男员工x人，女员工540-x人。依题意x+30=2（540-x），得到x=350，女员工有190人，男员工比女员工多160人，选C。

19、某篮球比赛14:00开始，13:30允许观众入场，但早有人来排队等候入场，假设从第一个观众来到时起，每分钟来的观众人数一样多，如果开3个入场口，13:45时就不再有人排队，如果开4个入场口，13:40就没有人排队，那么第一个观众到达的时间是：_____
A: 13:00B: 13:05C: 13:10D: 13:15
参考答案: A 本题解释:【答案】A。解析：设每个入场口每分钟可以进1人，则每分钟到达的观众为（3×15-4×10）÷（15-10）=1，到13:45时，总共有45人入场，需要45分钟，则第一个观众到达时间为13:00。

20、某班46个同学要在A、B、C、D、E五位候选人中选出一位体育委员。已知A得选票25张，B得选票占第二位，C、D得票相同，而E选票最少，只得4票。那么B得了多少张选票?_____
A: 7张B: 9张C: 6张D: 4张
参考答案: A 本题解释:【解析】由题干可知，B、C、D三人共得选票46-25-4=17（张）。设C、D每人得票数为m，B得票数为n，则有2m+n=17（n>m），则m=5，n=7。故B得选票为7张。

21、用1个70毫升和1个30毫升的容器盛取20毫升的水到水池A中，并盛取80毫升的酒精到水池B中，倒进或倒出某个容器都算一次操作，则最少需要经过几次操作_____
A: 15B: 16C: 17D: 18
参考答案: A 本题解释:【答案】A。解析：将30毫升的容器装满后倒人70时毫升的容器中，反复3次可以得到20毫升的水;将70毫升的容器装满后倒人30毫升的容器中，再倒出，两次之后可以得到lO毫升的酒精，再加上70毫升的酒精.得到80毫升的酒精。注意倒进和倒出各算一次操作，经过15次操作可以完成。

22、A、B两桶中共装有108公斤水。从A桶中取出1/4的水倒入B桶，再从B桶中取出1/4的水倒入A桶，此时两桶中水的重量刚好相等。问B桶中原来有多少公斤水？_____
A: 42B: 48C: 50D: 60
参考答案: D 本题解释:【解析】D。代入排除思想。由题意，最后两桶水中各有54公斤水。代入D项60。则A桶原有水量为48公斤，48×1/4=12,12+60=72,72×1/4=18，72-18=54，满足题意。

23、小明前三次数学测验的平均分数是88分，要想平均分数达到90分以上，他第四次测验至少要达到_____
A: 98分B: 96分C: 94分D: 92分
参考答案: B 本题解释:【解析】B。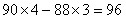分，该数值可以根据以上式子判定尾数为6，选择B。

24、小红把平时节省下来的全部五分硬币先围成一个正三角形，正好用完，后来又改围成一个正方形，也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币，则小红所有五分硬币的总价值是_____。
A: 1元 B: 2元 C: 3元 D: 4元
参考答案: C 本题解释:C。【解析】设三角形每条边X，正方形为Y，那么Y=X-5，同时由于硬币个数相同，那么3X=4Y，如此可以算出X=20，则硬币共有3×20=60个，硬币为5分硬币，那么总价值是5×60=300（分），得出结果。

25、甲、乙、丙三队在A、B两块地植树，A地要植树900棵，B地要植树1250棵，已知甲、乙、丙每天分别能植树24，30，32棵，甲在A地植树，丙在B地植树，乙先在A地植树，然后转到B地植树。两块地同时开始同时结束，乙应在开始后第几天从A地转到B地?_____
A: 5B: 7C: 9D: 11
参考答案: D 本题解释:D【解析】 植树共需（900+1250）÷（24+30+32）=25（天）。乙应在A地干（900-24×25）÷30=10（天），第11天转到B地。故本题正确答案为D。

26、一百张牌抽掉奇数牌，然后再抽掉剩下牌中位于奇数位的牌……如此最后剩下的一张是原来100张牌排序中的第几张呢？_____
A: 63 B: 64 C: 65 D: 66
参考答案: B 本题解释:B

27、计算：(1×2×3+2×4×6+…+100×200×300)/(2×3×4+4×6×8+…+200×300×400)的值为_____。
A: 1/8B: 1/4C: 3/2D: 5/4
参考答案: B 本题解释:B【解析】分析分子部分每个加数(连乘积)的因数，可以发现前后之间的倍数关系，从而把“1×2×3”作为公因数提到前面，分母部分也做类似的变形。原式=1×2×3+8×(1×2×3)+…+1000000×(1×2×3)2×3×4+8×(2×3×4)+…+1000000×(2×3×4)=[1×2×3×(1+8+…+1000000)]/[2×3×4×(1+8+…+1000000)]=(1×2×3)/(2×3×4)=1/4因此，本题正确答案为B。

28、有两根长短粗细不同的蚊香，短蚊香可燃8小时，长蚊香可燃的时间是短蚊香的1/2，同时点燃两根蚊香，经过3小时，它们的长短正好相等，未点燃之前，短蚊香比长蚊香短_____。
A: 1/6B: 1/5C: 1/2D: 3/5
参考答案: D 本题解释:D【解析】两根蚊香同时点燃3小时后所剩长度相等，从这里我们可以找出长、短蚊香的长度关系：短蚊香点燃3小时后剩1-1× 3/8=5/8，长蚊香点燃3小时后剩1-（1×3）/（8×1/2）=1/4，即短蚊香的5/8等于长蚊香的1/4，由此可求出短蚊香是长蚊香的几分之几，即5/8短=1/4长，短/长=2/5，所以未点燃之前，短蚊香比长蚊香短1-2/5=3/5。

29、某考试均为判断题,共10题,每题10分,满分为100分。考生答题时认为正确则画为“0”。认为不正确则画“×”。以下是考生的答题情况及甲、乙、丙的实际得分,则丁的得分为_____。题号12345678910得分甲××0×0××0××0乙×000×0×0000丙×000×××0×00丁××000××0000
A: 20分B: 40分C: 60分D: 80分
参考答案: C 本题解释:【答案】C。解析:首先观察甲和丙，得分相差40分，而他们的答案不一样的出恰好有4题，那么也就是说，丙和甲不一样的题(即2，4，5，10)甲都做对了，而这四道题恰好乙也全做错了，而乙一共做错了5道题，也就是说剩下的题目(1，3，7，8，6，9)中，乙只错了一个;又四人判断一致的题目，(即1，3，7，8)中必有一个四个人全做错了，因为丙一共只做对了3道题，那么，也就是说6、9、题乙做对了，那么现在答案除了1、3、7、8都确定了，即(2，4，5，10)与甲一致，(6，9)与乙一致,在这6道题中丁做对了3道,剩下的(1,3,7,8)丁做对3道。综上所述,丁得分60分。

30、四个相邻质数之积为17 017,他们的和为_____。
A: 48B: 52C: 61D: 72
参考答案: A 本题解释:【答案】A。解析:l7017=l7×l3×11×7,它们的和为48。

31、某单位举行“庆祝建党90周年”知识抢答赛，总共50道抢答题。比赛规定：答对1题得3分，答错1题扣1分，不抢答得0分。小军在比赛中抢答了20道题，要使最后得分不少于50分，则小军至少要答对_____道题。
A: 16 B: 17 C: 18 D: 19
参考答案: C 本题解释:C。假设答对x题，取最坏情形，剩下都答错，则答错20-x题，总分不少于50，则有3x-（20-x）≥50，求得x≥17.5，取最小值为18。

32、二十几个小朋友围成一圈，按顺时针方向一圈一圈地连续报数。如果报2和200的是同一个人，那么共有_____个小朋友。
A: 22B: 24C: 27D: 28
参考答案: A 本题解释:A【解析】小朋友的人数应是(200-2)=198的约数，而198=2×3×3×11。约数中只有2×11=22符合题意。

33、某一学校有500人，其中选修数学的有359人，选修文学的有408人，那么两种课程都选的学生至少有多少?_____。
A: 165人B: 203人C: 267人D: 199人
参考答案: C 本题解释:C【解析】若一人只选修一门课程，则至少有359+408=767(人)，但该学校只有500人，多出的767-500=267(人)则是选两门课程的。故正确答案为C。

34、某商店实行促销手段，凡购买价值200元以上的商品可以优惠20％，那么用300元钱在该商店最多可买下价值_____元的商品。
A: 350元B: 384元C: 375元D: 420元
参考答案: C 本题解释:C【解析】300/80%=375元。故选C。

35、某铁路线上有25个大小车站，那么应该为这条路线准备多少种不同的车票？_____
A: 500B: 600C: 400D: 450
参考答案: B 本题解释:【解析】B。25×24＝600

36、牧羊人正在放牧，一个人牵着一只羊问他。“你的羊群有多少只?”牧羊人答道：“这群羊加上一倍，再加上原来羊群的一半。又加上原来羊群的四分之一，算上你牵来的羊，正好满一百只。”请问，牧羊人的羊群有多少只?_____
A: 32只B: 34只C: 36只D: 38只
参考答案: C 本题解释:C[解析]“原来羊群的四分之一”说明羊群数可以被4整除，排除B、D项;代入答案得C项。

37、一根木杆，第一次截去了全长的1/2，第二次截去所剩木杆的1/3，第三次截去所剩木杆的1/4，第四次截去所剩木杆的1/5，这时量得所剩木杆长为6厘米。问：木杆原来的长是多少厘米?_____
A: 15B: 26C: 30D: 60
参考答案: C 本题解释: C解析： 6÷（1-1/5）÷（1-1/4）÷（1-1/3）÷（1-1/2）6÷（4/5×3/4×2/3×1/2）6÷1/5=30（厘米）故本题选C。

38、杯中原有浓度为18%的盐水溶液100ml，重复以下操作2次，加入100ml水，充分配合后，倒出100ml溶液，问杯中盐水溶液的浓度变成了多少？_____
A: 9%B: 7.5%C: 4.5%D: 3.6%
参考答案: C 本题解释:第一次操作后盐水浓度为，第二次操作后浓度为，故应选择C。

39、某城市一条大街长7200米，从起点到终点共设有9个车站，平均每两个车站之间的距离是多少米？_____。
A: 800 B: 900C: 850 D: 780
参考答案: B 本题解释:B 【解析】由于九个站点之间共有八段长度相等的距离，故两个站点之间的距离为7200÷8=900 （米）。

40、已知两个四位数的差为7930，问这两个四位数的和最大值为多少?_____
A: 12068B: 12560C: 13268D: 13650
参考答案: A 本题解释: 【答案】A。要使两数的和尽量的大，则应使这两个数尽量大，取较大的数为9999，则较小的为9999-7930=2069，它们的和等于9999+2069=12068，选A。

41、某校图书馆新购进120本图书，其中教育学类书60本，心理学类40本，有30本既不属于教育学类也不属于心理学类，则这批书中教育心理学书有多少本?_____
A: 10B: 20C: 30D: 40
参考答案: A 本题解释:A【解析】设教育心理学书购进X本。则根据两集合容斥原理核心公式可得︰60+40-x=120-30x=10，故答案为A选项。

42、三位采购员定期去某市场采购，小王每隔9天去一次，大刘每隔6天去一次，老杨每隔7天去一次，三人星期二第一次在这里碰面，下次相会将在星期几？_____
A: 星期一 B: 星期五 C: 星期二 D: 星期四
参考答案: C 本题解释: 【解析】C。取9，6，7的最小公倍数得126，即过126天，此三人才能再次相遇，而126天恰好是18个星期，因此下次他们见面还是在星期二。

43、某蓄水池有一进水口A和一出水口B,池中无水时，打开A口关闭B口，加满整个蓄水池需2个小时，池水满水时，打开B口关闭A口，放干池中水需1个小时30分钟，现池中有占总容量三分之一的水，问同时打开A、B口，需多长时间才能把蓄水池放干?_____
A: 90分钟B: 100分钟C: 110分钟D: 120分钟
参考答案: D 本题解释:【答案】D。

44、某商场开展购物优惠活动：一次购买300元及以下的商品九折优惠;一次购买超过300元的商品，其中300元九折优惠，超过300元的部分八折优惠。小王购物第一次付款144元，第二次又付款310元。如果他―次购买并付款，可以节省多少元?_____
A: 16B: 22.4C: 30.6D: 48
参考答案: A 本题解释:A【解析】统筹优化问题。由题意，第一次付款144元可得商品原价为160元;第二次付款为310元，可得原价为350元。故总价510元，按照优惠，需付款300×0.9+210×0.8=438元，节省了454-438=16元。

45、甲、乙两校共有毕业生180人，两校各买了一批纪念册，给本校毕业生每人一本后，甲校余116本，乙校余114本。经研究两校各向彼校毕业生每人送一本纪念册，送后甲校还比乙校多剩10本。问甲校的毕业生人数比乙校的毕业生人数多多少人?_____
A: 20人B: 16人C: 10人D: 8人
参考答案: D 本题解释:【解析】解一：由题意知，两校各给本校毕业生每人一本后共余下116+114=230本。两校再各向彼校毕业生每人送一本后共余下230-180=50本，而这时甲校比乙校多余下10本，故知此时甲校还余下（50+10）÷2=30本，乙校还余下（50-10）÷2=20本。而两校各给对方每个毕业生送了一本后，相当于两校买的纪念册各发了180本，所以甲校买了30+180=210本，乙校买了20+180=200本，甲、乙两校的毕业生人数分别是210-116=94人，200-114=86人。二者之差94-86=8人。故选D。解二：第一次分发毕业纪念册后，甲校余下的比乙校多116-114=2本，给彼校分发完毕后，甲校比乙校剩余的多10本，由此可推断甲校学生比乙校多10-2=8人，故选D。

46、某剧院有25排座位，后一排比前一排多2个座位，最后一排有70个座位。这个剧院一共有多少个座位?_____
A: 1104　B: 1150　C: 1170　D: 1280
参考答案: B 本题解释:B[解析]最后一排有70个坐位，则前面24排每一排少两个，第一排有70-24×2=22，构成一个等差数列，公差为2，首项为22，S25=25×22+(25×24×2)÷2=1150个，选择B。

47、某商场在节日期间实行促销，规定凡是购买200元以上的商品可以优惠20%，那么用300元钱在该商场最多可买下价值多少元的商品？_____
A: 375B: 350C: 340D: 320
参考答案: A 本题解释:A。购买200元以上可以优惠20%，即购买200元以上的商品可以打八折。

48、某班共有50名学生参加数学和外语两科考试，已知数学成绩及格的有40人，外语成绩及格的有25人，据此可知数学成绩及格而外语成绩不及格者_____。
A: 至少有10人B: 至少有15人C: 有20人D: 至多有30人
参考答案: B 本题解释:答案：B【解析】这是一个集合问题，首先可排除答案D，因为与已知条件“外语及格25人”即“外语不及格25人”不符;其次排除C，因为仅以外语及格率为50%推算数学及格者（40人）中外语不及格人数为40×50%=20（人），缺乏依据，实际上，数学及格者中外语不及格的人数至少为25-（50-40）=15人，答案为B。

49、有100人参加运动会的三个比赛项目，每人至少参加一项，其中未参加跳远的有50人，未参加跳高的有60人，未参加赛跑的有70人。问至少有多少人参加了不止一个项目？_____
A: 7B: 10C: 15D: 20
参考答案: B 本题解释:【解析】B。最值问题。由题意，参加跳远的人数为50人，参加跳高的为40人，参加赛跑的为30人；即参加项目的人次为120人次；故欲使参加不止一项的人数最少，则需要使只参加一项的人数最多为x，参加3项的人数为y；故x+3y=120，x+y=100，解得y=10。

50、一个两位数除以一个一位数，商仍是两位数，余数是8。问：被除数、除数、商以及余数之和是多少?_____
A: 98B: 107C: 114D: 125
参考答案: D 本题解释:【答案】D。解析：猜证结合的98÷10=9余8，10+98+9+8=125。

51、男女并排散步，女的3步才能跟上男的2步。两人从都用右脚起步开始到两人都用左脚踏出为止，女的应走出多少步？_____
A: 6步B: 8步C: 12步D: 多少步都不可能
参考答案: D 本题解释:【解析】D。两人的出脚顺序以6步为一个循环。在这6步中，两人没有一次同时出左脚，因此多少步都不可能。

52、有两只相同的大桶和一只空杯子，甲桶装牛奶，乙桶装糖水，先从甲桶内取出一杯牛奶倒入乙桶，再从乙桶取出一杯糖水和牛奶的混合液倒人甲桶，请问，此时甲桶内的糖水多还是乙桶内的牛奶多?_____。
A: 无法判定B: 甲桶糖水多C: 乙桶牛奶多D: 一样多
参考答案: D 本题解释:D【精析】假设乙桶内有N杯糖水，从甲中取出1杯牛奶倒入乙桶，乙桶中有l杯牛奶和N杯糖水。均匀后，再从乙桶取出一杯糖水和牛奶的混合物倒入甲桶，这杯混合物中有牛奶1/N+1杯有糖水N/N+1杯,因此乙桶中剩余的牛奶有N/N+1杯，而倒入甲桶中的糖水也有而N/N+1杯。甲桶内的糖水和乙桶内的牛奶一样多。

53、某日小李发现日历有好几天没有翻，就一次翻了6张，这6天的日期加起来的数字和是141，他翻的第一页是几号?_____
A: 18B: 21C: 23D: 24
参考答案: B 本题解释:B解析：设翻的第一页的日期为a，那么有：6a+，=141，解得a=21，选B。也可以利用中位项定理求解，141÷6=23.5，说明，排在第三和第四的分别是23号和24号，那么第一页应该是21号。

54、一个长方形，它的周长是32米，长是宽的3倍。这个长方形的面积是多少平方米?_____
A: 64B: 56C: 52D: 48
参考答案: D 本题解释:D设宽为x则长为3x，则2(x+3x)=32，则x=4，故面积为48平方米。

55、A、B两地相距1350米，甲和乙分别从A、B两地出发，相向而行。已知甲的速度为4千米/小时，乙的速度为5千米/小时，1分钟后两人调头反方向而行，再过3分钟，两人再次调头反方向而行，以此类推，再过5、7、……(连续奇数)分钟调头而行，请问，出发多少分钟后两人才能相遇?_____
A: 9B: 25C: 49D: 81
参考答案: D 本题解释:【答案解析】如果两人不调头走，两人相遇需要1350÷1000÷(4+5)×60=9分钟。如果以初始方向为正方向，则两个人分别走了1、-3、5、-7、……分钟的路程，由于9=1-3+5-7+9-11+13-15+17，则出发后1+3+5+7+9+11+13+15+17=81分钟两人相遇。

56、小明前三次数学测验的平均分数是88分，要想平均分数达到90分以上，他第四次测验至少要达到_____
A: 98分B: 96分C: 94分D: 92分
参考答案: B 本题解释: 【解析】B。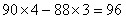分，该数值可以根据以上式子判定尾数为6，选择B。

57、某单位有员工540人，如果男员工增加30人就是女员工人数的2倍，那么原来男员工比女员工多几人？_____
A: 13B: 31C: 160D: 27
参考答案: C 本题解释:【答案】C。解析：男员工增加30人后，总员工为570人，男员工是女员工的2倍，得女员工为570÷3＝190，则原有男员工540－190＝350，男员工比女员工多350－190＝160人。故正确答案为C。老师点睛：男员工增加30人后，总员工为570人，男员工是女员工的2倍，由于540、30均为偶数，则原有男、女员工的数目也为偶数，男员工比女员工多的人数也是偶数。只有选项C符合条件，故正确答案为C。

58、毛毛骑在牛背上过河，他共有甲、乙、丙、丁4头牛，甲过河要2分钟，乙过河要3分钟，丙过河要4分钟，丁过河要5分钟。毛毛每次只能赶2头牛过河，要把4头牛都赶到对岸去，最少要多少分钟? _____
A: 16B: 17C: 18D: 19
参考答案: A 本题解释:A。若要时间最短，则一定要让耗时最长的两头牛同时过河。先骑甲、乙过河，骑甲返回，共用5分钟;再骑丙、丁过河，骑乙返回，共用8分钟;最后再骑甲、乙过河，用3分钟，共用时5+8+3=16分钟。

59、某人在雅虎上申请了一个邮箱，邮箱密码是由0至9中任意4个数字组成，他任意输入4个数字，输入正确密码的概率是_____。
A: 10　B: 10　C: 10　D: 10
参考答案: B 本题解释:B[解析]正确的密码只有一个，这10个数字的组合共有10个，所以答案是B。

60、某盒灯泡中有3只次品和6只正品(每只均可区分)，测试员每次取出一只进行测试，直到3只次品全部测出为止。假如第三只次品在第六次测试时被发现，那么不同的测试情况共有多少种？_____
A: 43200B: 7200C: 60D: 120
参考答案: B 本题解释:B。

61、某车间从3月2日开始每天调入人，已知每人每天生产～件产品，该车间从月1日至3月21日共生产840个产品.该车间应有多少名工人? _____
A: 20B: 30C: 35D: 40
参考答案: B 本题解释:【答案】B。解析：从3月2日开始调入的每一个人生产的产品的个数正好组成以1为公差的等差数列20，19，18，……1，得调入的人生产的总产品数是：(20+1)×20÷2=210(个)，所以原有工人生产的产品数=840-210=630(个)，每人每天生产一个，所以工人数=630/21=30(个)。

62、现有边长1米的一个木质正方体，已知将其放入水里，将有0.6米浸入水中。如果将分割成边长0.25米的小正方体，并将所有的小正方体都放入水中，直接和水接触的表面积总量为_____。
A: 3.4平方米B: 9.6平方米C: 13.6平方米D: 16平方米
参考答案: C 本题解释:本题属于面积问题。因为把边长为1米的正方体木块置于水中有0.6米浸入水中，所以当将其分割为边长0.25米的正方体木块置于水中时，其浸入水中的高度为3/20米。则可以计算出其中一个分割后的正方体木块与水的接触面积为：（1/4）×（1/4）+4×（1/4）×（3/20）=1/16+3/20,又因为边长1米的正方体可以分割为64个边长为O.25米的正方体，所以题中所求面积为：64×（1/16+3/20）=13.6（平方米）。正确答案为C。

63、袋子里装有红、蓝两色的小球各12个,先从袋子中拿出一个球,然后将它放回袋子中,混合后再从中拿出一个小球。那么两次抽中不同颜色的小球的几率有_____。
A: 20%B: 25%C: 50%D: 60%
参考答案: C 本题解释:【解析】因为两种颜色的小球数量相等,那么每次抽中其中一种颜色小球的概率均为50%。第一种情况:第一次抽中了红色小球,第二次抽中了蓝色小球,概率是50%×50%一25%;第二种情况:第一次抽中了蓝色小球,第二次抽中了红色小球,概率是50%×50%=25%。那么两次抽中不同颜色的小球的整体概率等于两种情况下的概率之和,即25%+25%=50%,答案为C。

64、取甲种硫酸300克和乙种硫酸250克，再加水200克，可混合成浓度为50％的硫酸；而取甲种硫酸200克和乙种硫酸150克，再加上纯硫酸200克，可混合成浓度为80%的硫酸。那么，甲、乙两种硫酸的浓度各是多少？_____
A: 75%，60%B: 68%，63%C: 71%，73%D: 59%，65%
参考答案: A 本题解释:【答案】A。解析：

65、60名员工投票从甲、乙、丙三人中评选最佳员工，选举时每人只能投票选举一人，得票最多的人当选。开票中途累计，前30张选票中，甲得15票，乙得10票，丙得5票。问在尚未统计的选票中，甲至少再得多少票就一定当选?_____
A: 15B: 13C: 10D: 8
参考答案: B 本题解释:最值问题。构造最不利，由题意，还剩30名员工没有投票，考虑最不利的情况，乙对甲的威胁最大，先给乙5张选票，甲乙即各有15张选票，其余25张选票中，甲只要在获得13张选票就可以确定当选。

66、心灵投射谬误也称为投射作用，它是一种非形式谬误，有两种形式，一种形式是某人认为他看世界的观点反映了世界的真相。也就是，某人将他的个人感觉投射到真实世界；另一种形式是某人认为自己不了解一个现象意味着这现象无法被理解或不是真的。根据上述定义，下列不属于心灵投射谬误的是_____。
A: 小李忍受不了闻臭豆腐的味道，就说臭豆腐这么臭，没人会喜欢吃B: 小敏是重庆人，到上海工作后，他发现上海菜普遍是甜的，于是他逢人就说上海菜很难吃C: 尽管知道葡萄架上的葡萄很甜，但是小刘因为摘不到，就对别人说葡萄很酸D: 课间，小荣给大家讲了一个冷笑话，小明理解不了为什么大家听后都捧腹大笑，就说小荣讲的笑话一点水平都没有
参考答案: C 本题解释:【答案】C。解析：心灵投射谬误有两种形式，一种是强调自己的主观意识，即认为自己的观点就是事情的真相。另一种认为自己不了解的就是无法理解的或不是真的。C项小刘的行为是自欺欺人的表现，他对别人说葡萄很酸，但自己并没有认为葡萄是酸的，因为他知道葡萄很甜，不符合“心灵投射谬误”的定义，故本题选C。

67、某医院有一氧气罐匀速漏气，该氧气罐充满后同时供40人吸氧，60分钟后氧气耗尽，再次充满该氧气罐同时供60个人吸氧，则45分钟后氧气耗尽。问如果该氧气罐充满后无人吸氧，氧气耗尽需要多长时间？_____
A: 1.5小时B: 2小时C: 2.5小时D: 3小时
参考答案: D 本题解释:【答案】D。解析：这是一个变形的牛吃草问题。设原有氧气为M，漏气速度为V，则可得（40＋V）×60＝（60＋V）×45＝M，解得V＝20，M＝3600，如果没人吸氧，则可得耗尽的时间为3600÷20＝180分钟，即3小时。故正确答案为D。

68、画一个边长为2cm的正方形，再以这个正方形的对角线为边画第二个正方形，再以第二个正方形的对角线为边画第三个正方形，则第三个正方形面积为_____平方厘米。
A: 32B: 16C: 8D: 4
参考答案: C 本题解释:C由题可知第2个正方形对角线长为2cm;则第三个正方形的面积为（2）2=8（平方厘米）;正确答案为C。

69、有7个不同的质数,他们的和是58,其中最小的质数是多少?_____。
A: 2B: 3C: 5D: 7
参考答案: A 本题解释:【答案】A。解析:除了2以外的质数全是奇数,如果7个数全是奇数的话,他们的和不会是58这个偶数,所以,7个数中必然有2,而2是所有质数中最小的一个。(2、3、5、7、11、13,17这7个质数的和为58)

70、分数4/9、17/35、101/203、3/7、151/301中最大的一个是_____。
A: 4/9B: 17/35C: 101/203D: 151/301
参考答案: D 本题解释:D【解析】选取中间值法，所有分数都接近1/2，1/2-4/9=1/18，1/2-17/35=1/70，1/2-101/203=1/406，1/2-3/7=1/14，1/2-151/301=-1/602，显然151/301大于1/2，故选D。

71、一段路程分为上坡、平路、下坡，三段路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米，路程全长是50千米，小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A 本题解释:A解析：上坡、平路、下坡的速度之比是：14∶25∶36=5∶8∶10平路速度为：3×8/5=24/5（千米/小时）下坡速度为：3×10/5=6（千米/小时）上坡路程为：50×1/（1+2+3）=50/6=25/3（千米）平路路程为：50×2/（1+2+3）=50/3（千米）下坡路程为：50×3/（1+2+3）=25（千米）小龙走完全程用的时间为：25/3÷3+50/3÷24/5+25÷6=10（5/12）（小时）故本题选A。

72、123456788×123456790-123456789×123456789=_____。
A: 0B: 1C: 2D: -1
参考答案: D 本题解释: D [解析] 原式=（123456789-1）×（123456789+1）-1234567892=1234567892-1-1234567892=-1故选D。

73、药厂使用电动研磨器将一批晒干的中药磨成药粉。厂长决定从上午10点开始，增加若干台手动研磨器进行辅助作业。他估算如果增加2台，可在晚上8点完成，如果增加8台，可在下午6点完成。问如果希望在下午3点完成，需要增加多少台手工研磨器？_____
A: 20B: 24C: 26D: 32
参考答案: C 本题解释:【答案】C。解析：设原有电动研磨器为N台，需要增X台手工研磨器，根据牛吃草公式有：Y=(N+2)10;Y=(N+8)8，解得N=22，Y=240;代入Y=(N+X)5解得X=26，故选择C选项。

74、两只蜗牛由于耐不住阳光照射，从井顶走向井底，白天往下走，一只蜗牛一个白天能走20厘米，另一只只能走15厘米;黑夜里往下滑，两只蜗牛下滑速度相同，结果一只蜗牛5昼夜到达井底，另一只却恰好用了6昼夜。问井深是多少厘米?_____
A: 150B: 180C: 200D: 250
参考答案: A 本题解释:A【解析】两只蜗牛白天路程差为20×5-15×6=10（厘米）。因为最终到达井底，所以蜗牛黑夜下滑的速度为每夜10÷（6-5）=10（厘米）。井深为（20+10）×5=150（厘米）。因此，正确答案为A。

75、100人列队报数，报单数的离队，留下的再依次报数，报单数的再离队，这样重复多次，直到最后只留下一个人，请问此人在第一次报数时是第几号?_____
A: 32B: 50C: 64D: 100
参考答案: C 本题解释:C。第一次报数后，留下队员的号数是：2，4，6，8…96，98，100，均为的倍数;第二次报数后，留下队员的号数是：4，8，12…96，100，均为的倍数;第五次报数之后，留下队员的号数是的倍数;第六次报数之后，留下队员的号数四的倍数可见最后余下的一人在第一次报数时是第64号。

76、某市出租车运费计算方式如下：起步价2公里6元，2公里之后每增加1公里收费1.7元，6公里之后每增加1公里收费2.0元，不足1元按四舍五入计算。某乘客乘坐了31公里，应该付多少元车费？ _____
A: 63 B: 64 C: 65 D: 66
参考答案: A 本题解释:A。2公里以内收费6元；2－6公里收费1.7×4＝6.8元；6－31公里收费2×25＝50元。因此总计应付车费62.8元，四舍五入即63元。故选A项。

77、四个相邻质数之积为17 017,他们的和为_____。
A: 48B: 52C: 61D: 72
参考答案: A 本题解释:【答案】A。解析:l7017=l7×l3×11×7,它们的和为48。

78、一项工程由甲单独做需要15天做完，乙单独做需要12天做完，二人合做4天后，剩下的工程由甲单独做，还需做几天方可做完？_____。
A: 6 B: 8C: 9 D: 5
参考答案: A 本题解释:A 【解析】依题意，甲每天完成总工程的1／15，乙每天完成总工程的1／12，甲、乙合作4天共完成（1／12+1／15） ×4=3／5，故剩下的工程甲需要的时间为（1—3／5）／（1／15）=6，总计算式即为[1一（1／12+1／15）]×4／（1／15）=6（天）。

79、

80、小新做一道加法题，由于粗心将一个加数万位上的3看成8，百位上的1看成7，个位上的9看成6，算得的结果是95050。则这道加法题的正确答案本应是_____。
A: 44447B: 45453C: 44453D: 45405
参考答案: C 本题解释:C【解析】本题只要找出错看的加数和本来的加数之间的差值，用错误结果加上少加的数，减去多加的数，即可得出正确结果。即正确答案=95050-（80000-30000）-（700-100）+（9-6）=95050 -50000-600+3=44453由此可知本题正确答案为C。

81、用直线切割一个有限平面，后一条直线与此前每条直线都要产生新的交点。第1条直线将平面分成2块，第2条直线将平面分成4块，第3条直线将平面分成7块，按此规律将该平面分为22块需：_____
A: 5条直线B: 6条直线C: 7条直线D: 8条直线
参考答案: A 本题解释:增加的面的个数：交第一条直线，分割两个面，以后交一条直线，则增加的面的个数为交点增加数加1，即（n-1+1） = n 故对n条直线，面数为 n + （n-1） + …… + 2 + 2 = n（n+1）/2 +1 注意：开始面上只有1条直线时已有2个面，故最小为2。总结下：对第n条直线： 面数：n（n+1）/2 +1 故答案为6。

82、从一楼走到五楼，爬完一层休息30秒，一共要210秒，那么从一楼走到7楼，需要多少秒_____
A: 318B: 294C: 330D: 360
参考答案: C 本题解释:答案：C 解析：从一点走到五楼，休息了三次，那么每爬上一次需要的时间为（210-30×3）÷（5-1）=30秒，故从一楼走到七楼需要30×（7-1）+30×（7-2）=330秒。

83、一堆沙重480吨，用5辆载重相同的汽车运3次，完成了运输任务的25%，余下的沙由9辆同样的汽车来运，几次可以运完？_____
A: 4次B: 5次C: 6次D: 7次
参考答案: B 本题解释:【答案】B。解析：因为用5辆载重相同的汽车运3次，完成了运输任务的25%，所以每辆车一次可以运总工程量的（25÷5÷3）％＝（5/3）％，所以9辆车一次可以运总工程量的9×（5/3）％＝15％，余下的75％用9辆车运的话需要75÷15＝5次，故正确答案为B。

84、从装满1000克浓度为50%的酒精瓶中倒出200克酒精，再倒人蒸馏水将瓶加满。这样反复三次后，瓶中的酒精浓度是_____。
A: 22.5%B: 24.4%C: 25.6%D: 27.5%
参考答案: C 本题解释:C【解析】每次操作后，酒精浓度变为原来的（1000-200）÷1000=0.8，故反复三次后浓度变为50%×0.8×0.8×0.8=25.6%。

85、计算：(2+4+6+8+…+2010)-(1+3+5+7+…+2009)=_____。
A: 995B: 1011C: 1111D: 1005
参考答案: D 本题解释:【解析】原式=（2-1）+（4-3）+（6-5）+（8-7）+…+（2010-2009）=1+1+1+1+…+1从2到2010共有1005个偶数,所以原式等于1005个1相加,等于1005,故本题答案为D。

86、商场的自动扶梯以匀速由下往上行驶，两个孩子嫌扶梯走得太慢，于是在行驶的扶梯上，男孩每秒钟向上走2个梯级，女孩每2秒钟向上走3个梯级。结果男孩用40秒钟到达，女孩用50秒钟到达。则当该扶梯静止时，可看到的扶梯梯级有_____。
A: 80级 B: 100级 C: 120级 D: 140级
参考答案: B 本题解释:B。【解析】男孩所走的台阶数为40×2=80，女孩所走的台阶数为50/2×3=75，那么电梯的速度就应该为（80-75）/（50-40）=0.5，电梯所经过的台阶就为40×0.5=20， 电梯经过的台阶加上男孩经过的台阶，就是电梯的台阶数，即100级。

87、若干学校联合进行团体操表演，参演学生组成一个方阵，已知方阵由外到内第二层有104人，则该方阵共有学生_____人。
A: 625B: 841C: 1024D: 1369
参考答案: B 本题解释:【答案】B。解析：根据方阵公式：最外层人数＝4×最外层每边人数﹣4可知：由外到内第二层每排的学生数＝（104＋4）÷4＝27个；最外一层每排有学生＝27+2＝27+2＝29个；所以该方阵共有学生：29×29＝841个，故正确答案为B。

88、小明和小强从400米环形跑道的同一点出发，背向而行。当他们第一次相遇时，小明转身往回跑;再次相遇时，小强转身往回跑;以后的每次相遇分别是小明和小强两人交替调转方向。小明每秒跑3米，小强每秒跑5米，则在两人第30次相遇时。小明共跑了多少米? _____
A: 11250B: 13550C: 10050D: 12220
参考答案: A 本题解释:A。两人相向运动，经过400÷（3+5）=50秒相遇，之后小明转身，两人做追及运动，经过400÷（5-2）=200秒第二次相遇;接着两人又做相向运动，经过50秒相遇，再做追及运动，经过200秒相遇，以此类推，第30次相遇共用30÷2×（50+200）=3750秒，则小明共跑了3×3750=11250米。

89、一杯糖水，第一次加入一定量的水后，糖水的含糖百分比变为15%；第二次又加入同样多的水，糖水的含糖百分变比为12%；第三次再加入同样多的水，糖水的含糖百分比将变为多少？_____
A: 8%B: 9%C: 10%D: 11%
参考答案: C 本题解释:【答案】C。解析：故正确答案为C。

90、某单位有宿舍11间，可以住67人，已知每间小宿舍住5人，中宿舍住7人，大宿舍住8人，则小宿舍间数是_____。
A: 6B: 7C: 8D: 9
参考答案: A 本题解释:【答案】A。解析：设小宿舍有x间，中宿舍有y间，大宿舍有11-x-y间。依题意5x+7y+8（11-x-y）=67，得到3x+y=21。〔化为标准形式〕因为x、y均是大于0的整数，所以x＜7。直接选A。〔确定解的范围〕

91、如图所示，半圆与等腰三角形ABC的斜边AC相切，AB=BC=1。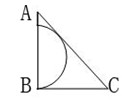问半圆的直径是多少?_____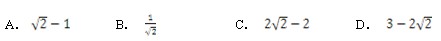
A: AB: BC: CD: D
参考答案: C 本题解释:C

92、某公司面试员工，其中五分之二的应聘者获得了职位。最终录取者的平均分比录取线高7分，落选者的平均分比录取线低13分，所有应聘者的平均分为58分，则该公司的招聘录取分数线是多少？_____
A: 60B: 63C: 65D: 69
参考答案: B 本题解释:【答案】B。解析：设招聘的录取线是X，录取者的平均分为X+7，落选者的平均分为X-13，设共有5个应聘者，则录取者2个，所以，录取者总的得分2（X+7）;落选者3个，落选者总的得分3（X-13）分;所有应聘者的得分为5分，所以，58×5=2（X+7）+3（X-13），可得X=63，可知答案为B。

93、商场销售某种商品的加价幅度为其进货价的40%，现商场决定将加价幅度降低一半来促销，商品售价比以前降低了54元。问该商品原来的售价是多少元？_____
A: 324B: 270C: 135D: 378
参考答案: D 本题解释:假设进价是10份，则原来售价是14份，现在售价是12份。差2份是54元，那么14份是54×7=378（元）。

94、我国民间常用十二生肖进行纪年，十二生肖的排列顺序是：鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪。2011年是兔年，那么2050年是_____。
A: 虎年B: 龙年C: 马年D: 狗年
参考答案: C 本题解释:C。从2011年增加到2050年，需要增加39年，其中前36年为12的倍数，在周期过程中不予考虑。因此2050年为兔向后数3年，即为马年。故选C。

95、1至1000中所有不能被5、6、8整除的自然数有多少个?_____
A: 491B: 107C: 400D: 600
参考答案: D 本题解释: D【解析】 只要求出1～1000内5的倍数、6的倍数或8的倍数或5×6，5×8，24，120的倍数，再根据容斥原理就可求得5的倍数有5、10……1000共200个6的倍数有6、12……996共166个8的倍数有8、16……共125个24的倍数有24、48……984共41个30的倍数有30、60……990共33个40的倍数有40、80……1000共25个120的倍数有120、240……960共8个根据容斥原理可知，5或6或8的倍数有（200+166+125）-（33+25+41）+8=400（个）不能被5或6或8中任一个整除的有1000-400=600（个）故本题选D。

96、一个三位数，各位上的数的和是15，百位上的数与个位上的数的差是5，如颠倒各位上的数的顺序，则所成的新数比原数的3倍少39。求这个三位数。_____
A: 196B: 348C: 267D: 429
参考答案: C 本题解释:【解析】C。代入法。首先排除A和D;根据所成的新数比原数的3倍少39，用每个选项的最后一个数乘以3再减去，所得的数只有C中有。

97、某公司一季度有82%的人全勤，二季度有87%的人全勤，三季度有96%的人全勤，四季度有93%的人全勤。那么全年全勤的人最多占_____，最少占_____。
A: 82%，42%B: 82%，58%C: 87%，58%D: 87%，42%
参考答案: B 本题解释:B【解析】当一季度全勤的人在其他三个季度也是全勤时，全年全勤人数的比例最高，即占82%。一季度没有全勤的人数占18%，二季度没有全勤的人数占13%，三季度没有全勤的人数占4%，四季度没有全勤的人数占7%，因此全年至少有1-（18%+13%+4%+7%）=58%的人全勤，故本题答案为B。

98、一容器内有浓度为30%的糖水，若再加入30千克水与6千克糖，则糖水的浓度变为25%。问原来糖水中含糖多少千克_____
A: 15千克 B: 18千克 C: 21千克 D: 24千克
参考答案: B 本题解释:【解析】B。设原来糖水有10x千克，含糖3x千克，则现在糖水有（10x＋36）千克，含糖（3x＋6）千克。由题意有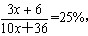，解得x=6，则3x=18，即原来糖水中含糖18千克。

99、某次飞机模型竞赛设一、二、三等奖。已知：(1)甲、乙两班获一等奖的人数相等;(2)甲班获一等奖的人数占该班获奖总人数的百分数与乙班相应的百分数的比为5:6;(3)甲、两班获二等奖的人数总和占两班获奖人数总和的20%;(4)甲班获三等奖的人数占该班获奖人数的50%;(5)甲班获二等奖的人数是乙班获二等奖人数的4.5倍。那么，乙班获一等奖的人数占该班获奖总人数的百分比为多少?_____
A: 60%B: 45%C: 32%D: 24%
参考答案: D 本题解释:

100、某项工程，甲单独完成需要8天，乙需要4天，甲做一半换乙，乙做剩余一半又换甲，甲又做剩余一半再换乙完成。问整个工程花费_____天。
A: 5.5 B: 6 C: 6.5 D: 7
参考答案: C 本题解释:C。假设工作总量为8，则甲每天完成1，乙每天完成2，甲先完成一半需要4÷1＝4天，乙完成剩下一半需要2÷2＝1，甲又做剩余一半需要1÷1＝1天，剩下乙完成需要1÷2＝0.5天，因此共需要6.5天。