1、某商店实行促销手段，凡购买价值200元以上的商品可以优惠20％，那么用300元钱在该商店最多可买下价值_____元的商品。
A: 350元B: 384元C: 375元D: 420元
参考答案: C 本题解释:C【解析】300/80%=375元。故选C。

2、某企业有甲、乙、丙三个仓库，且都在一条直线上，之间分别相距1千米、3千米，三个仓库里面分别存放货物5吨、4吨、2吨。如果把所有的货物集中到一个仓库，每吨货物每千米运费是90元，请问把货物放在哪个仓库最省钱?_____
A: 甲B: 乙C: 丙D: 甲或乙
参考答案: B 本题解释:B解析：此题遵循“小往大处靠”原则，先把2吨的货物移动到4吨那，这样就相当于有了6吨货物，然后在把5吨的货物也移动到6吨，综上所述，运到乙仓库最省钱。

3、77个连续自然数的和是7546，则其中第45个自然数是_____。
A: 91B: 100C: 104D: 105
参考答案: C 本题解释:77个自然数的和是7546，故平均数7546÷77＝98为中位数，也即第39个数，因此第45个数为104。故选C。

4、某单位职工24人中，有女性11人 ，已婚的有16人。已婚的16人中有女性6人。问这个单位的未婚男性有多少人?_____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释: B 解析：由题意：未婚共有：24-16=8人，其中未婚女性有：11-6=5人，故未婚男性有：8-5=3人，选B。

5、王家村西瓜大丰收后，全村男女老少分四个组品尝西瓜，且每组人数正好一样多，小伙子一人吃1个，姑娘两人吃1个，老人三人吃1个，小孩四人吃1个，一共吃了200个西瓜。则王家村品尝西瓜的共有_____。
A: 368人B: 384人C: 392人D: 412人
参考答案: B 本题解释:【答案】B。解析：解法一：设每组有x人，可列方程x+x/2+x/3+x/4＝200，解得x=96，则品尝西瓜的人数有96×4=384人。因此，本题答案为B选项。解法二：利用整除关系。由题意，全村人数必须能被3和8整除，只有B满足。因此，本题答案为B选项。

6、一个正方体木块放在桌子上，每一面都有一个数，位于对面两个数的和都等于13，小张能看到顶面和两个侧面，看到的三个数和为18;小李能看到顶面和另外两个侧面，看到的三个数的和为24，那么贴着桌子的这一面的数是多少_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:【答案】B。解析：小张、小李二人看到的数加起来一共为2组对面加上2倍的顶面，因此顶面为(18+24-13×2)÷2=8，底面为13-8=5.

7、地球表面的陆地面积和海洋面积之比是29︰71，其中陆地的四分之三在北半球，那么南、北半球海洋面积之比是_____
A: 284︰29B: 113︰55C: 371︰313D: 171︰113
参考答案: D 本题解释:【解析】D。根据题干中的比例关系，可以推断出南、北半球的海洋面积之比为：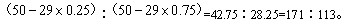

8、足球比赛的记分规则为：胜一场得3分;平一场得1分;负一场得0分。一个队打了14场，负5场，共得19分，那么这个队胜了几场?_____
A: 3B: 4C: 5D: 6
参考答案: C 本题解释:C解析：设这个队胜了a场，平了b场，则3a+b=19，a+b=14-5=9;解得a=5。

9、200除500，商2余100，如果被除数和除数都扩大3倍，则余数是_____。
A: 100B: 200C: 300D: 100000
参考答案: C 本题解释:【解析】商不变，余数跟着扩大3倍，所以是300，选C。

10、某儿童艺术培训中心有5名钢琴教师和6名拉丁舞教师，培训中心将所有的钢琴学员和拉丁舞学员共76人分剐平均地分给各个老师带领，刚好能够分完，且每位老师所带的学生数量都是质数。后来由于学生人数减少，培训中心只保留了4名钢琴教师和3名拉丁舞教师，但每名教师所带的学生数量不变，那么目前培训中心还剩下学员多少人？_____
A: 36B: 37C: 39D: 41
参考答案: D 本题解释:【答案】D。解析：假定每个钢琴教师带x个学生，每个拉丁舞教师带y个学生，则根据题意有：5x＋6y＝76。根据此方程，可知x必为偶数，而x与y均为质数，因此x＝2，代回可得y＝11。于是在学生人数减少后，还剩下学员为4×2＋3×11＝41个，故正确答案为D。

11、李明从图书馆借来一批图书，他先给了甲5本和剩下的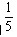，然后给了乙4本和剩下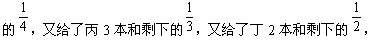，最后自己还剩2本。李明共借了多少本书?_____
A: 30B: 40C: 50D: 60
参考答案: A 本题解释: 【解析】A。解法一、设李明共借书x本，则，解得x=30;解法二、思维较快的直接倒推用反计算，。

12、共有20个玩具交给小王手工制作完成。规定，制作的玩具每合格一个得5元，不合格一个扣2元，未完成的不得不扣。最后小王共收到56元，那么他制作的玩具中，不合格的共有_____个。
A: 2B: 3C: 5D: 7
参考答案: A 本题解释:【答案】A。解析：设小王制作合格玩具x个，不合格玩具y个，未完成的有z个。则x＋y＋z＝20，5x－2y＝56。为不定方程组，将选项代入验证，仅当y＝2时，x与z有正整数解。故正确答案为A。

13、一间长250米、宽10米、高4米的仓库放置了1000个棱长为1米的正方体箱子，剩余的空间为_____立方米。 B: 1500C: 5000D: 9000
参考答案: D 本题解释:【答案】D。解析：仓库的容量为250×10×4＝10000立方米，1000个棱长为1米的正方体箱子体积为1000×1×1×1＝1000立方米，则剩余空间为10000－1000＝9000平方米，故正确答案为D。

14、定义：①群体互补效应：由不同年龄、专业、智能水平、气质类型的人才有机地组成一个结构合理的人才群体，达到知识互用、能力互补，使只有专才的个体，变成多能的人才群。②群体协调效应：在结构合理的人才群体中，逐步形成了群体每个成员共同遵守的良好的道德规范和传统作风，以此调节和协调群体中个体与个体、个体与群体、群众与社会的关系，并影响和控制整个群体，使群体的力量和功能得到维护和加强。③群体感应效应：在结构合理的人才群体中，人才之间在目标上志同道合，在学风上互相感染，在学术上互相影响，同心同德，紧密团结，创新意识和创造思维不断激化和强化，形成对人才创造特别有利的“微型气候”。典型例证：(1)某大学有效整合资源，在校内外组织多方面人才，团结协作，集体攻关。(2)正因为好大学有优良的校风和传统，所以人人才都想上好大学。(3)小李做事低调，从不张扬。上述典型例证与定义存在对应关系的数目有_____。
A: 0个B: 1个C: 2个D: 3个
参考答案: C 本题解释:【答案】C。解析：第一步：抓住每个定义中的关键词群体互补效应：关键词强调“不同年龄、专业、智能水平、气质类型的人才”、“知识互用、能力互补”。群体协调效应：关键词强调“群体每个成员共同遵守”、“调节和协调”。群体感应效应：关键词强调“目标上志同道合，在学风上互相感染，在学术上互相影响”。第二步：逐一分析例证与定义间的关系例证（1）大学组织了多方面的人才，形成群体互补效应，对应定义①，例证（2）好大学因为有优良的校风和传统而受欢迎，属于群体感应效应，对应定义③；例证（3）讲的是小李的个体行为，与上面的定义均不相符。例证与定义存在对应关系的数目有2个，故正确答案为C。

15、某天晚上一警局18%的女警官值班。如果那天晚上有180个警官值班，其中一半是女警官，问该警局有多少女警官？_____
A: 900B: 180C: 270D: 500
参考答案: D 本题解释:【解析】D。180个警官中的一半是女警官，则值班的女警官为90个，而这90个女警官占总数的女警官18％，可知女警官有500人。

16、下列哪项能被11整除? _____
A: 937845678B: 235789453C: 436728839D: 867392267
参考答案: A 本题解释:A【解析】9+7+4+6+8=343+8+5+7=2334-23=11所以，答案是A。

17、某单位举办庆国庆茶话会，买来4箱同样重的苹果，从每箱取出24千克后，结果各箱所剩的苹果重量的和，恰好等于原来一箱的重量。那么原来每箱苹果重多少千克?_____
A: 16B: 24C: 32　D: 36
参考答案: C 本题解释:【答案】C。解析：取出4×24=96千克苹果，相当于4-1=3箱的重量，则原来每箱苹果重96÷3=32千克。

18、有一种用六位数表示日期的方法是：从左到右的第一、第二位数表示年，第三、第四位数表示月，第五、第六位数表示日，例如890817表示1989年8月17日。如果用这种方法表示1991年的日期，那么全年中有6个数都不同的日期共有多少天?_____
A: 99B: 90C: 30D: 20
参考答案: C 本题解释:【解析】因为有91，所以1、9、10、11、12月都不能出现，实际上，2月因为0、1、2、均已出现，9102XX也是不行的，（第一个X应为0、1、2中之一）。在剩下的6个月中，每个月都有5天，共5×6=30天，例如：三月份：910324，910325，910326，910327，910328。

19、单独完成某项工作，甲需要16小时，乙需要12小时，如果按照甲、乙、甲、乙……的顺序轮流工作，每次1小时，那么完成这项工作需要多长时间?_____
A: 13小时40分钟B: 13小时45分钟C: 13小时50分钟D: 14小时
参考答案: B 本题解释:答案：B.[解析]本题为工程类题目。设总工程量为48，则甲的效率是3，乙的效率是4，工作12小时后，完成了42。第12小时甲做了3，完成了总工程量45，剩余的3由乙在第十四小时完成。在第十四小时里，乙所用的时间是3/4小时，所以总时间是13.75小时。

20、用0，1，2，…，9这10个数字组成一个四位数，一个三位数，一个两位数与一个一位数，每个数字只许用一次，使这四个数的和等于2007，则其中三位数的最小值为_____。
A: 386B: 260C: 230D: 204
参考答案: D 本题解释:D。

21、某人以96元的价格出售了两枚古铜币，一枚挣了20%，一枚亏了20%。问：此人盈利或亏损的情况如何？_____
A: 挣了8元 B: 亏了8元 C: 持平 D: 亏了40元
参考答案: B 本题解释: 【解析】B。96×2-[96÷（1+20%）+96÷（1-20%）]=192-200=-8，亏了8元。

22、办公室有甲、乙、丙、丁4位同志，甲比乙大5岁，丙比丁大2岁。丁三年前参加工作，当时22岁。他们四人现在的年龄之和为127岁。那么乙现在的年龄是_____
A: 25岁B: 27岁C: 35岁D: 40岁
参考答案: C 本题解释:答案：C【解析】根据题意，丁现在25岁，丙现在27岁，甲和乙共127-27-25=75岁，甲比乙大5岁，所以乙现在（75-5）÷2=35岁。

23、从一楼走到五楼，爬完一层休息30秒，一共要210秒，那么从一楼走到7楼，需要多少秒？_____
A: 318B: 294C: 330D: 360
参考答案: C 本题解释:【答案】C。解析：从一楼走到五楼，休息了3次，那么每爬上一层需要的时间为（210－30×3）÷4＝30秒，故从一楼走到七楼需要30×（7－2）＋30×（7－1）＝330秒。故正确答案为C。

24、将一根绳子连续对折三次，然后每隔一定长度剪一刀，共剪6刀。问这样操作后，原来的绳子被剪成几段？_____
A: 18段B: 49段C: 42段D: 52段
参考答案: B 本题解释:【答案】B。解析：对折三次，则绳子变成8折，在上面剪6刀，第一刀为8*1+1=9段；第二刀为8*2+1=17段，依次类推第六刀为8*6+1=49段，因此绳子被剪成49段。因此正确答案为B。

25、某大型项目考察团队的所有员工年龄都在26～35岁之间，问：改考察团队至少有多少人才能保证在同一年出生的有5人？_____
A: 41B: 49C: 50D: 51
参考答案: A 本题解释:【答案】A。解析：最不利情况就是每年出生的人都有4个人，做题方法：最不利的情况数+1=4×10+1=41

26、一个金鱼缸，现已注满水。有大、中、小三个假山，第一次把小假山沉入水中，第二次把小假山取出，把中假山沉入水中，第三次把中假山取出，把小假山和大假山一起沉入水中。现知道每次从金鱼缸中溢出水量的情况是：第一次是第二次的1/3，第三次是第二次的2倍。问三个假山的体枳之比是多少？_____
A: 1：3：5 B: 1：4：9 C: 3：6：7 D: 6：7：8
参考答案: B 本题解释:【答案】B。解析：本题的关键是要注意第二次把中假山放入水里的时候，浴缸水不满，缺少的部分恰好是小假山的体积。已知第一次溢出的水是第二次溢出的水的1/3，即第二次溢出的水的体积是中假山和小假山的体积差，可以推导出小假山与中假山体积比为1:4，此时可直接选出正确答案为B。

27、某车间从3月2日开始每天调入人，已知每人每天生产～件产品，该车间从月1日至3月21日共生产840个产品.该车间应有多少名工人? _____
A: 20B: 30C: 35D: 40
参考答案: B 本题解释:【答案】B。解析：从3月2日开始调入的每一个人生产的产品的个数正好组成以1为公差的等差数列20，19，18，……1，得调入的人生产的总产品数是：(20+1)×20÷2=210(个)，所以原有工人生产的产品数=840-210=630(个)，每人每天生产一个，所以工人数=630/21=30(个)。

28、小王的手机通讯录上有一手机号码，只记下前面8个数字为15903428。但他肯定，后面3个数字全是偶数，最后一个数字是6，且后3个数字中相邻数字不相同，请问该手机号码有多少种可能? _____
A: 15B: 16C: 20D: 18
参考答案: B 本题解释:答案：B 解析：根据题意，倒数第二个数字有0、2.、4、8四种可能;倒数第三个数字同样有4种可能（只需与倒数第二个数字不同即可），故该手机号为4×4=16种可能。

29、一个9×11个小矩形组成的大矩形一共有多少个矩形? _____
A: 2376B: 1188C: 2970D: 3200
参考答案: C 本题解释:C【解析】矩形是由横向2条平行线，纵向2条平行线相互垂直构成的。9×11的格子，说明是10×12条线。所以我们任意在横向和纵向上各取2条线就能构成一个矩形。答案就是 C10取2×C12取2=2970。

30、将10克盐和200克浓度为5%的盐水一起加入一杯水中，可得浓度为2.5%的盐水，则原来杯中水的克数是_____。
A: 570B: 580C: 590D: 600
参考答案: C 本题解释:C。

31、甲、乙、丙三人钱数各不相同，甲最多，他拿出一些钱给乙和丙，使乙和丙的钱数都比原来增加了两倍，结果乙的钱最多；接着乙拿出一些钱给甲和丙，使甲和丙的钱数都比原来增加了两倍，结果丙的钱最多；最后丙拿出一些钱给甲和乙，使甲和乙的钱数都比原来增加了两倍，结果三人钱数一样多了。如果他们三人共有81元，那么三人原来的钱分别是多少元？_____
A: 20，11，50 B: 19，7，55 C: 12，9，60 D: 11，15，55
参考答案: B 本题解释:B。【解析】三人最后一样多，所以都是81÷3=27元，然后我们开始还原：1.甲和乙把钱还给丙：每人增加2倍，就应该是原来的3倍，所以甲和乙都是27÷3=9，丙是81-9-9=63；2.甲和丙把钱还给乙：甲9÷3=3，丙63÷3=21，乙81-3-21=57；3.最后是乙和丙把钱还给甲：乙57÷3=19，丙21÷3=7，甲81-19-7=55元。

32、将60拆成10个质数之和，要求其中最大的质数尽可能小，那么这个最大的质数是多少？_____
A: 5B: 7C: 11D: 13
参考答案: B 本题解释:B。最大的质数必大于5，否则10个质数之和将不大于50。所以最大的质数最小为7，且7的个数尽可能多。60÷7＝8……4，而4＝2＋2，所以60可以分拆成8个7和两个2的和。故满足条件的最大的质数最小为7。

33、由1、2、3组成的没有重复数字的所有三位数之和为多少？_____
A: 1222 B: 1232 C: 1322 D: 1332
参考答案: D 本题解释:D。因为1、2、3之和可被3整除，故而1、2、3所组成的没有重复数字的三位数都能被3整除，而这些数字相加之和也必能被3整除，只有D项能被3整除，为正确答案。根据排列组合原理，可知该没有重复数字的三位数共有6个，1、2、3三个数在个、十、百位上各出现两次，即（1+2+3）×2=12，也就是说这一数字当为12+120+1200=1332。

34、某试卷共25题，答对的，一题得4分;答错或不答的，一题扣1分，小王得了60分，则小王答对了多少题?_____
A: 14B: 15C: 16D: 17
参考答案: D 本题解释: D [解析] 设答对了x道题，则未答对的题为（25-x）题，可得4x-（25-x）×1=60，解得x=17。故本题选D。

35、用2、4、5、7这4个不同数字可以组成24个互不相同的四位数，将它们从小到大排列，那么7254是第多少个数?_____
A: 19B: 20C: 18D: 17
参考答案: B 本题解释:【解析】由已知得每个数字开头的数各有24÷4=6个，从小到大排列，7开头的从第6×3+1=19个开始，易知第19个是7245，第20个是7254。

36、某条道路的一侧种植了51棵梧桐树，其中道路两端各有一棵，且相邻两棵树之间的距离相等。如果需要在这一侧再多种10棵树，且通过移动一部分树(不含首尾两棵)使所有相邻两棵树之间的距离仍然相等，则这51棵树中至少有多少棵不需要移动位置？_____
A: 9B: 10C: 11D: 12
参考答案: C 本题解释:【答案】C。解析：设路长为50×60米，则第一次的间距为60米，第二次的间距为50米，不需要移动位置的树距起点的距离必须为60和50的公倍数，即距离应是300的倍数。总长为3000米，则中间有9棵树不需要移动，再加上首尾两棵，一共有11棵树不需要移动。因此，本题选择C选项。

37、一段路程分为上坡、平路、下坡三段，路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米，路程全长是50千米，小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A 本题解释:A解析：上坡、平路、下坡的速度之比是：14∶25∶36=5∶8∶10平路速度为：3×8/5=24/5(千米/小时)下坡速度为：3×10/5=6(千米/小时)上坡路程为：50×1/(1+2+3)=50/6=25/3(千米)平路路程为：50×2/(1+2+3)=50/3(千米)下坡路程为：50×3/(1+2+3)=25(千米)25/3÷3+50/3÷24/5+25÷6=10(5/12)(小时)故本题选A。

38、如果两个四位数的差等于8921，那么就说这两个四位数组成一个数对，问这样的数对共有多少个?_____
A: 80B: 79C: 83D: 81
参考答案: B 本题解释:【解析】从两个极端来考虑这个问题：最大为9999-1078=8921，最小为9921-1000=8921，所以共有9999-9921+1=79个，或1078-1000+1=79个。故应选择B。

39、有甲乙丙三种盐水，浓度分别为5%、8%、9%，质量分别为60克、60克、47克，若用这三种盐水配置浓度为7%的盐水100克，则甲种盐水最多可用_____
A: 49克B: 39克C: 35克D: 50克
参考答案: A 本题解释:【答案】A。解析：

40、某人登山,上山时每走30分钟,休息10分钟;下山时每走30分钟,休息5分钟;下山的速度是上山速度的1.5倍。如果下山用了2小时15分,那么上山用的时间是_____。
A: 3小时40分B: 3小时50分C: 4小时D: 4小时10分
参考答案: B 本题解释:【答案】B。解析:设上山速度是1,下山的速度是1.5,下山的时间是135分钟,那么走了4个30分钟,休息了3个5分钟,也就是走了2小时,那么路程就是1.5×2=3,上山时速度是1,时间就是3÷1=3小时,也就是走了6个30分钟,这需要休息5个10分钟,总共就用了3小时50分钟。

41、某地收取手机费的标准是：每月打电话不超过30分钟，每分钟收费5角;如果超出30分钟，超出部分按每分钟7角收费。已知某月甲比乙多交了3元3角的手机费，则该月甲、乙两人共打了多少分钟电话?_____
A: 63B: 62C: 61D: 60
参考答案: A 本题解释:如果甲、乙两人打电话都超过30分钟，那么相差的电话费就应该是7的倍数，显然33不是7的倍数;如果甲、乙两人打电话都没超过30分钟，那么相差的电话费就应该是5的倍数，显然33不是5的倍数，因此只有一种情况：甲超过了30分钟，乙未达到30分钟。因为只有33=5×1+7×4一种情况满足题意，故甲打电话时间为30+4=34（分钟），乙打电话时间为30一1=29（分钟），甲、乙两人共打了34+29=63（分钟）。故选A。

42、一次知识竞赛，共3道题，每个题满分6分。给分时只能给出自然数0—6分。如果参加竞赛的人三道题的得分的乘积都是36分，并且任意两人三道题的得分不完全相同，那么最多有多少人参加竞赛? _____
A: 24B: 20C: 18D: 12
参考答案: D 本题解释:【解析】D。解析：36=1×6×6=2×3×6=3×3×4，三道题得1，6，6分有3种可能，三道题得2，3，6分有6中可能，三道题得3，3，4分有3种可能。故最多有3+6+3=12人。

43、小明今年a岁，芳芳明年(a-4)岁，再过c年，他们相差_____。
A: 4岁B: c+4岁C: 5岁D: c-3岁
参考答案: C 本题解释:【解析】不管过多少年，两人年龄差永远不会改变;今年芳芳是a-5岁，所以相差5岁，选C。

44、a=8.8+8.98+8.998+8.9998+8.99998，则a的整数部分是_____。
A: 45B: 44C: 43D: 42
参考答案: B 本题解释:B 【解析】因为a>8.8×5=44，a<9×5=45，所以a的整数部分是44。

45、试求出下边图形中阴影部分的面积_____。
A: 3B: 2C: 1.5D: 11
参考答案: B 本题解释:【答案】B。解析:图形正中间的正方形边长为2,那么它的面积为4。阴影面积为它的一半,所以是2。

46、有一批书要打包后邮寄，要求每包内所装书的册数都相同，用这批书的7/12打了14个包还多35本，余下的书连同第一次多的零头刚好又打了11包，这批书共有多少本?_____
A: 1000B: 1310C: 1500D: 1820
参考答案: C 本题解释: C 解析： 由已知条件，全部书的7/12打14包还多35本，可知全部书的1/12打2包还多5本，即全部书的5/12打10包还多25本，而余下的是5/12加35本打11包。所以，（35+25）÷（11-10）=60本，1包是60本，这批书共有（14+11）×60=1500（本）。故本题正确答案为C。

47、32头牛和若干匹马的价钱相等，如果把牛的头数和马的头数互换，马的头数再减少14头，此时二者的价钱又相等了。请问，每头牛和马的价格比为多少？_____
A: 2∶1 B: 3∶2 C: 4∶3 D: 3∶4
参考答案: D 本题解释:【答案】D。解析：设32头牛和x匹马的价钱相同，则交换后，x头牛和32-14=18头马的价钱相同，则32∶x=x∶18，解得x=24。故每头牛和马的价格比为24∶32=3∶4。

48、四人进行篮球传接球练习，要求每人接到球后再传给别人，开始由甲发球，并作为第一次传球。若第五次传球后，球又回到甲手中，则共有传球方式多少种：_____
A: 60;B: 65;C: 70;D: 75;
参考答案: A 本题解释:【答案解析】：选A，球第一次与第五次传到甲手中的传法有：C(1,3)×C(1,2)×C(1,2)×C(1,2)×C(1,1)=3×2×2×2×1=24，球第二次与第五次传到甲手中的传法有：C(1,3)×C(1,1)×C(1,3)×C(1,2)×C(1,1)=3×1×3×2×1=18，球第三次与第五次传到甲手中的传法有：C(1,3)×C(1,2)×C(1,1)×C(1,3)×C(1,1)=3×2×1×3×1=18，24+18+18=60种，具体而言：分三步：(1)在传球的过程中，甲没接到球，到第五次才回到甲手中，那有3×2×2×2=24种，第一次传球，甲可以传给其他3个人，第二次传球，不能传给自己，甲也没接到球，那就是只能传给其他2个人，同理，第三次传球和第四次也一样，有乘法原理得一共是3×2×2×2=24种。(2)因为有甲发球的，所以所以接下来考虑只能是第二次或第三次才有可能回到甲手中，并且第五次球才又回到甲手中。当第二次回到甲手中，而第五次又回到甲手中，故第四次是不能到甲的，只能分给其他2个人，同理可得3×1×3×2=18种。(3)同理，当第三次球回到甲手中，同理可得3×3×1×2=18种。最后可得24+18+18=60种

49、某商场举行周年让利活动，单件商品满300减180元，满200减100元，满100减40元;若不参加活动则打5.5折。小王买了价值360元，220元，150元的商品各一件，最少需要多少元钱?_____
A: 360B: 382.5C: 401.5D: 410
参考答案: B 本题解释:【答案】B。解析：如下表：因此最少需要180+120+82.5=382.5元。

50、有4支队伍进行4项比赛，每项比赛的第一、第二、第三、第四名分别得到5、3、2、1分。每队的4项比赛得分之和算作总分，如果已知各队的总分不相同，并且A队获得了三项比赛的第一名，问总分最少的队伍最多得多少分? _____
A: 7B: 8C: 9D: 10
参考答案: B 本题解释:【答案】B 解析∶四项比赛的总得分是（5+3+2+1）×4=44分，A已得15分，最少得16分，剩下三人总得分最多为28分，要求得分最少的人得分最多且得分互不相同，则三人得分分别是8，9，11。此时一人得三项第二和一项第三，一人得一项第二和三项第三。

51、某区要从10位候选人中投票选举人大代表，现规定每位选举人必须从这10位中任选两位投票，问至少要有多少位选举人参加投票，才能保证有不少于10位选举人投了相同两位候选人的票?_____
A: 382位B: 406位C: 451位D: 516位
参考答案: B 本题解释:【答案】B。解析：从10位候选人中选2人共有种票，则每种票有9张相同时需要×9=405个

52、幼儿园里，老师将一堆桃子分给同学，如果每个同学分3个则余2个，如果每个同学分4个，则有两个同学分不到，该班有多少个同学?_____
A: 10B: 12C: 15D: 18
参考答案: A 本题解释:A【解析】设共有x个同学，由题意得3x+2=4（x-2），解得x=10。

53、10个人欲分45个苹果，已知第一个人分了5个，最后一人分了3个，则中间的8人一定存在连续的两人至少分了_____个苹果。
A: 8B: 9C: 10D: 11
参考答案: C 本题解释:【答案】C。解析：中间的8人共分得苹果45—5—3＝37（个），将中间的8人分为4组，即（第2、3个人）（第4、5个人）（第6、7个人）（第8、9个人）。由37＝9×4+1可知，必有1组，即连续的两人分到了10个苹果。故答案为C。

54、一个学雷锋小组的大学生们每天到餐馆打工半小时，每人可挣3元钱。到11月11日，他们一共挣了1764元。这个小组计划到12月9日这天挣足3000元捐给“希望工程”。因此小组必须在几天后增加一个人。增加的这个人应该从11月_____日起每天到餐馆打工，才能到12月9日恰好挣足3000元钱。
A: 18B: 24C: 14D: 20
参考答案: D 本题解释:D[解析]还缺3000-1764=1236（元），从11月12日～12月9日还有30+9-12+1=28（天），这28天中，（原来小组中）每人可挣3×28=84（元）。因为1236÷84=14……60，所以原有14人，必须增加一个人挣60元。60÷3=20（天），30+9-20+1=20，所以增加的这个人应该从11月20日起去打工。

55、把一根钢管锯成两端要4分钟，若将它锯成8段要多少分钟?_____
A: 16B: 32C: 14D: 28
参考答案: D 本题解释:【解析】D。锯成2段只需要锯1次，即每次需要4分钟，而锯8段需要锯7次，7×4=28，所以正确答案为D。

56、甲、乙两车运一堆货物。若单独运，则甲车运的次数比乙车少5次;如果两车合运，那么各运6次就能运完，甲车单独运完这堆货物需要多少次_____
A: 9B: 10C: 13D: 15
参考答案: B 本题解释:【答案】B。解析：工程问题。设甲单独需要x，则乙单独需要x+5，依题意有1/x+1/(x+5)=1/6,解得x=10。

57、在同一环形跑道上小陈比小王跑得慢，两人都按同一方向跑步锻炼时，每隔12分钟相遇一次；若两人速度不变，其中一人按相反方向跑步，则隔4分钟相遇一次。问两人跑完一圈花费的时间小陈比小王多几分钟？_____
A: 5B: 6C: 7D: 8
参考答案: B 本题解释:不妨设小王和小陈速度分别为x，y，跑道长度为s，则：两人都按同一方向跑步锻炼时，每隔12分钟相遇一次，说明s/（x—y）=12;若两人速度不变，其中一人按相反方向跑步，则每隔4分钟相遇一次，说明s/（x+y）=4;解得s=6x=12y，所以两人跑完一圈花费的时间小陈比小王多6分钟。

58、一容器内有浓度为30%的糖水，若再加入30千克水与6千克糖，则糖水的浓度变为25%。问原来糖水中含糖多少千克_____
A: 15千克 B: 18千克 C: 21千克 D: 24千克
参考答案: B 本题解释:【解析】B。设原来糖水有10x千克，含糖3x千克，则现在糖水有（10x＋36）千克，含糖（3x＋6）千克。由题意有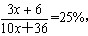，解得x=6，则3x=18，即原来糖水中含糖18千克。

59、某月刊每期定价5元。某单位一部分人订半年，另一部分人订全年，共需订费480元；如果订半年的改订全年，订全年的改订半年，那么共需420元。共有多少人订了这份期刊？_____
A: 25B: 20C: 15D: 10
参考答案: D 本题解释:D。所有人订一年半期刊所花的钱为（480＋420）元，则订了这份期刊的人数为（480＋420）＋[5×（6＋12）]＝10个人。

60、任意取一个大于50的自然数，如果它是偶数，就除以2;如果它是奇数，就将它乘3之后再加1。这样反复运算，最终结果是多少? _____
A: 0B: 1C: 2D: 3
参考答案: B 本题解释:【答案】B 解析∶特殊值法，取64，按题意，最后结果为l。也可用排除法，最后结果显然不能为0;若为2，按题意，需再计算一次，得到l;若为3，需继续运算，最后结果也将是1。

61、Ａ大学的小李和B大学的小孙分别从自己学校同时出发，不断往返于A、B两校之间。现已知小李的速度为85米/分，小孙的速度为105米/分，且经过12分钟后两人第二次相遇。问A,B两校相距多少米?_____
A: 1140米B: 980米C: 840米D: 760米
参考答案: D 本题解释:易知到第二次相遇时，两人合起来走过的距离恰为A、B两校距离的3倍，因此A、B两校相距（85+105）×12÷3=760（米）。故选D。

62、某市出租车收费标准是：5千米内起步费10.8元，以后每增加1千米增收1.2元，不足1千米按1千米计费。现老方乘出租车从A地到B地共支出24元，如果从A地到B地先步行460米，然后再乘出租车也是24元，那么从AB的中点C到B地需车费_____元。(不计等候时间所需费用)
A: 12B: 13.2C: 14.4D: 15.6
参考答案: C 本题解释:经济M题。共花钱24元，超过5千米的部分为24-10.8=13.2（元），超过5千米后走了13.2÷1.2=11（千米），总路程最多为16千米，因为步行460米后花费相同，说明460米后的路程一定超过15千米，则总路程15+0.46<S≤16，则C到B的距离7.73<< p>S/2≤8，因不足1千米按1千米计费，故应看成8千米，共花费10.8-9（8-5）×1.2=14.40（元）。

63、某乐队举办一场演唱会的收入是7000元,乐队的主唱分得其中的25%,另外5名成员平分余下的收入,那么他们每人分得多少元?_____
A: 1750B: 1400C: 1120D: 1050
参考答案: D 本题解释:【答案】D。解析:主唱分25%,其余5人分75%,所以每人分15%,所以7000×l5%=1050元。

64、某三年制普通初中连续六年的在校生人数分别为：X1,X2,X3,X4,X5,X6.假设该校所有学生都能顺利毕业，那么前三年的入学学生总数与后三年的入学学生总数之差为_____
A: (X1+X2+X3)-(X4+X5+X6) B: X1-X4C: X3-X6 D: (X3-X1)-(X6-X4)
参考答案: C 本题解释:【解析】C.考查整体思维。前三年入学学生人数本质上就是第三年的在校生人数X3（第三年在校生的初三、初二、初一分别为前三年的入学人数），类似的，X6即为后三年的入学人数。故答案为X3-X6.

65、某公司一季度有82%的人全勤，二季度有87%的人全勤，三季度有96%的人全勤，四季度有93%的人全勤。那么全年全勤的人最多占_____，最少占_____。
A: 82%，42%B: 82%，58%C: 87%，58%D: 87%，42%
参考答案: B 本题解释:B【解析】当一季度全勤的人在其他三个季度也是全勤时，全年全勤人数的比例最高，即占82%。一季度没有全勤的人数占18%，二季度没有全勤的人数占13%，三季度没有全勤的人数占4%，四季度没有全勤的人数占7%，因此全年至少有1-（18%+13%+4%+7%）=58%的人全勤，故本题答案为B。

66、某校下午2点整派车去某厂接劳模作报告，往返须1小时。该劳模在下午1点整就离厂步行向学校走来，途中遇到接他的车，便坐上车去学校，于下午2点40分到达。问汽车的速度是劳模的步行速度的几倍? _____
A: 4B: 6C: 7D: 8
参考答案: D 本题解释:D。【解析】本题要画图辅助，假设全程距离为1，汽车来回的时间为1小时，所以，其速度为1，汽车运行时间为2/3小时，所以汽车跑的路程为2/3，人走的距离为剩下1/3路程的一半，即1/6，步行的时间为1小时20分，所以步行的速度是1/6÷（1+1/3）=1/8，所以汽车的速度是劳模的8倍。选D。

67、某种皮衣定价是1150元，以8折售出仍可以盈利15%，某顾客在8折的基础上要求再让利150元，如果真是这样，商店的盈亏情况是：_____
A: 亏20元B: 赚20元C: 亏30元D: 赚30元
参考答案: C 本题解释:【答案】C。解析：该皮衣的成本为1150×0.8÷（1+15%）=800元，在8折的基础上再让利150元的收入为1150×0.8-150=770元，所以商店会亏损800-770=30元。

68、如图所示，半圆与等腰三角形ABC的斜边AC相切，AB=BC=1。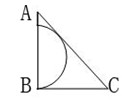问半圆的直径是多少?_____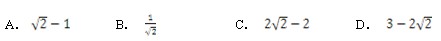
A: AB: BC: CD: D
参考答案: C 本题解释:C

69、甲、乙两地相距100千米，张先骑摩托车从甲出发，1小时后李驾驶汽车从甲出发，两人同时到达乙地。摩托车开始速度是50千米/小时，中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟，那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 1(1/2)C: 1/3D: 2
参考答案: C 本题解释:C解析：汽车行驶100千米需100÷80=1（1/4）（小时），所以摩托车行驶了1（1/4）+1+,1/6=2（5/12）（小时）。如果摩托车一直以40千米/小时的速度行驶，2（5/12）小时可行驶96（2/3）千米，与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷（50-40）=1/3（小时）。故本题选C。

70、将700克14.3%的盐水与900克11.1%的盐水混合后，再加入200克盐，蒸发掉300克水后，该盐水的浓度为_____。
A: 22.2%B: 24.3%C: 26.7%D: 28.6%
参考答案: C 本题解释:【答案】C。解析：由题意可得，最后该盐水浓度为（700×14.3%＋900×11.1%＋200）÷（700＋900＋200－300）＝400÷1500≈26.7%。故正确答案为C。

71、有一个上世纪80年代出生的人，如果他能活到80岁，那么有一年他的年龄的平方数正好等于那一年的年份。问此人生于哪一年_____
A: 1980年 B: 1983年 C: 1986年 D: 1989年
参考答案: A 本题解释:【解析】A。1980～2069中只有一个平方数2025（即），由“有一年他的年龄的平方数正好等于那一年的年份”可知满足条件的那一年是2025年，此时他的年龄为45岁，因此此人生于2025-45=1980（年），符合“上世纪80年代出生”这个要求。

72、船在流速为每小时1000米左右的河上逆流而上，行至中午12点时，有一乘客的帽子落到了河里。乘客请求船家返回追赶帽子，这时船已经开到离帽子100米远的上游。已知在静水中这只船的船速为每分钟20米。假设不计调头的时间，马上开始追赶帽子，问追回帽子应该是几点几分？_____
A: 12点10分B: 12点15分C: l2点20分D: 12点30分
参考答案: A 本题解释:【解析】A。本题不需要考虑水速。船和帽子的相对速度为每分钟20米，距离相差100米，可得追上帽子需要5分钟；发现帽子到返回追帽子船走了100米，此段路程所花的时间为5分钟，则追回帽子应该是12点10分。

73、

74、5个男生和3个女生排成一排，3个女生必须排在一起，有多少种不同排法？_____
A: 240B: 320C: 450D: 480
参考答案: B 本题解释: 答案【B】采用捆绑法，把3个女生视为一个元素，与5个男生进行排列，共有 A（6，6）=6x5x4x3x2种，然后3个女生内部再进行排列，有A（3，3）=6种，两次是分步完成的，应采用乘法，所以排法共有：A（6，6） ×A（3，3） =320（种）。

75、20＋19－18－17＋16＋15－14－13＋12＋11···＋4＋3－2－1＝_____。
A: 10B: 15C: 19D: 20
参考答案: D 本题解释:【答案】D。解析：解析1：原式＝（20－18）＋（19－17）＋（16－14）＋（15－13）＋···＋（4－2）＋（3－1）＝2＋2＋2＋2＋···＋2＋2＝2×10＝20。故正确答案为D。解析2：原式＝20＋（19－18－17＋16）＋（15－14－13＋12）＋…＋（3－2－1）＝20。故正确答案为D。

76、在一次国际美食大赛中，中、法、日、俄四国的评委对一道菜品进行打分。中国评委和法国评委给出的平均分是94，法国评委和日本评委给出的平均分是90，日本评委和俄罗斯评委给出的平均分是92，那么中国评委和俄罗斯评委给出的平均分是_____。
A: 93分B: 94分C: 96分D: 98分
参考答案: C 本题解释:C【解析】设中、法、日、俄四国的评委给出的分数分别是A、B、C、D，根据题意可知：A+B=94×2，B+C=90×2，C+D=92×2，又因为A+D=（A+B）+（C+D）-（B+C）=94×2+92×2-90×2=（94+92-90）×2=96×2所以中国评委和俄国评委给出的平均分是96分，本题正确答案为C。

77、出租车在开始10千米以内收费10.5元，以后每走1千米，收费1.7元。请问走25千米需收多少钱?_____
A: 20.6元　B: 35元　C: 36.5元D: 36元
参考答案: D 本题解释:D

78、从一楼走到五楼，爬完一层休息30秒，一共要210秒，那么从一楼走到7楼，需要多少秒_____
A: 318B: 294C: 330D: 360
参考答案: C 本题解释:答案：C 解析：从一点走到五楼，休息了三次，那么每爬上一次需要的时间为(210-30×3)÷(5-1)=30秒，故从一楼走到七楼需要30×(7-1)+30×(7-2)=330秒。

79、一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的2倍，那么这个长方体的表面积是_____
A: 74B: 148C: 150D: 154
参考答案: B 本题解释:【解析】B。设该长方体的长、宽、高分别是。那么有所以这个长方体的表面积为

80、分数4/9、17/35、101/203、3/7、151/301中最大的一个是_____。
A: 4/9B: 17/35C: 101/203D: 151/301
参考答案: D 本题解释:D【解析】首先目测可以知道3/7、17/35和101/203都小于1/2，而4/9和151/301都大于1/2，所以只要比较二者的大小就可以，通过计算，151/301大，所以选择D。

81、某月刊杂志，定价2.5元，劳资处一些人订全年，其余人订半年，共需510元，如果订全年的改订半年，订半年的改订全年，共需300元，劳资处共多少人？_____
A: 20 B: 19 C: 18 D: 17
参考答案: C 本题解释: 【解析】本题用解方程的方法也可以解答，但是速度较慢。由题意可知，如果劳资处所有人都订一年半的话，总计810元;而单人订一年半的月刊需元;所以共有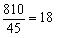人。故选C。

82、有关部门要连续审核30个科研课题方案，如果要求每天安排审核的课题个数互不相等且不为零，则审核完这些课题最多需要_____。
A: 7天B: 8天C: 9天D: 10天
参考答案: A 本题解释:【答案解析】1+2+3+4+5+6+7=28，再加一个2等于30，但因为是要互不相等，所以8天的情况和更多的情况都不符合，只能是7天，也就是1+2+3+4+5+6+9的情况，选A。

83、某单位举行“庆祝建党90周年”知识抢答赛，总共50道抢答题。比赛规定：答对1题得3分，答错1题扣1分，不抢答得0分。小军在比赛中抢答了20道题，要使最后得分不少于50分，则小军至少要答对_____道题。
A: 16 B: 17 C: 18 D: 19
参考答案: C 本题解释:C。假设答对x题，取最坏情形，剩下都答错，则答错20-x题，总分不少于50，则有3x-（20-x）≥50，求得x≥17.5，取最小值为18。

84、某人在雅虎上申请了一个邮箱，邮箱密码是由0至9中任意4个数字组成，他任意输入4个数字，输入正确密码的概率是_____。
A: 10　B: 10　C: 10　D: 10
参考答案: B 本题解释:B[解析]正确的密码只有一个，这10个数字的组合共有10个，所以答案是B。

85、在1至1000的1000个自然数中，既不是4的倍数，也不是6的倍数的数共有多少个?_____
A: 375B: 416C: 625D: 791
参考答案: C 本题解释:C【解析】1000÷4=250（个），所以1至1000中4的倍数的数有250个。1000÷6=166……4，所以1至1000中6的倍数的数有166个。1000÷（4×6）=41……16，说明1至1000中既是4的倍数，又是6的倍数的数有41个。即4的倍数的个数与6的倍数的个数的交集有41个，如图所示。所以1至1000中，既是4的倍数，也是6的倍数的数共有209+125+41=375（个）。则1至1000中，既不是4的倍数，也不是6的倍数的数共有：1000-（209+125+41）=1000-375=625（个）。故本题选C。

86、一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的2倍，那么这个长方体的表面积是_____
A: 74B: 148C: 150 D154
参考答案: B 本题解释: 【解析】B。设该长方体的长、宽、高分别是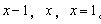。那么有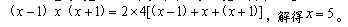所以这个长方体的表面积为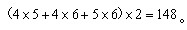

87、19991998的末位数字是：_____
A: 1 B: 3 C: 7 D: 9
参考答案: A 本题解释:【解析】此题关键是要考察末位数的变化情况，9的一次幂、二次幂、三次幂、四次幂……的尾数呈9、1、9、1……变化，即其奇数次幂时尾数是9，偶数次幂时尾数是1，所以，选A

88、把自然数n的各位数字之和记为Sn，如n=38，Sn=3+8=11。若对某些自然数n满足n-Sn=2007，则n最大值是_____。
A: 2010B: 2016C: 2019D: 2117
参考答案: C 本题解释:C【解析】当n-Sn=2007时，n为20ab的形式，依题意有20ab-（2+a+b）=2007，可得2000+10a+b-2-a-b=2007，得出a=1。当b取最大值9时，n有最大为2019。故选C。

89、5，3，7三个数字可以组成几个三位数?_____。
A: 8个B: 6个C: 4个D: 10个
参考答案: B 本题解释:B【解析】百位上的数可以在5,3，7三个数中选一个，有3种选法;在确定百位上的数后，十位上的数只有两种选法;百位上和十位上的数确定以后，个位上的数只有一种选法。所以三位数的组成方法共有3×2×1=6(种)。故正确答案为B。

90、7个同学排成两排照相，前排3人，后排4人，共有_____种站法。
A: 1680B: 2400C: 2520D: 5040
参考答案: D 本题解释:【解析】相当于把7个元素放在预先指定好的7个不同位置上，因此，是7个同学的全排列，共有P77=5040种站法。

91、四个相邻质数之积为17017，他们的和为_____
A: 48B: 52C: 61D: 72
参考答案: A 本题解释:答案：A【解析】17017分解因数为17×13×11×7，他们的和为48。

92、41个学生要坐船过河，渡口处只有一只能载4人的小船(无船工)，他们要全部渡过河去，至少要使用这只小船渡河多少次_____
A: 23B: 24C: 27D: 26
参考答案: C 本题解释:【答案】C。解析：4个人渡过去，1个人回来，因此每2次渡河可以渡过去3个学生.41=3×13+2，因此一共需要13×2+1=27次。

93、一个班有50名学生，他们的名字都是由2个或3个字组成的。将他们平均分为两组之后，两组的学生名字字数之差为10。此时两组学生中名字字数为2的学生数量之差为_____。
A: 5B: 8C: 10D: 12
参考答案: C 本题解释:C【解析】不定方程问题。由题意两组学生名字字数相差10，两边人数相同，即其中一组比另一组三名字人数多10人，则2名字人数少10人。

94、小王的手机通讯录上有一手机号码，只记下前面8个数字为15903428。但他肯定，后面3个数字全是偶数，最后一个数字是6，且后3个数字中相邻数字不相同，请问该手机号码有多少种可能？_____
A: 15B: 16C: 20D: 18
参考答案: B 本题解释:后三位全是偶数，且三数中相邻数字不同，已知最后一位是6，所以倒数第二位有0、2、4、8四种可能，倒数第三位也有四种可能性，故该手机号码有4×4=16（种）可能。

95、某工厂11月份工作忙，星期六、日不休息，而且从第一天开始，每天下班后都从总厂陆续派相同人数的工人到分厂工作，直到月底下班后，总厂还剩工人238人。如果月底统计总厂工人的工作量是8070个工作日(1人工作1天为1个工作日)，且无1个缺勤，那么，这个月由总厂派到分厂工作的工人共多少人？_____
A: 46人B: 30人C: 60人D: 62人
参考答案: C 本题解释:11月份有30天。设每天下班后派往分厂的人数为2，则根据题意可知，最后一天总厂的工作量为238+z，可列方程238+x+238+2x+…+238+30x=8070，解得x=2，即每天派2人到分厂工作，11月份30天共派了60人到分厂。故答案为C。

96、小王和小李合伙投资，年终根据每人的投资进行分红，小王取了全部的1/3另加9万元，小李取剩余1/3和剩下的14万元。问小王比小李多得多少万元_____
A: 0B: 1C: 2D: 3
参考答案: B 本题解释:B【解析】小李取剩下的1/3和剩下的14万元，即说明小李获得了14×3/2=21万元。又因为小王取了全部的1/3另加9万元，所以分红共有（21+9）×3/2=45万元。因此小王获得了45-21=24万元，所以小王比小李多得24-21=3万元。

97、如是2003除以一个两位数后，所得余数最大，则这个两位数为_____。
A: 92B: 82C: 88D: 96
参考答案: D 本题解释:D【解析】 2003÷99=20……2323+20×3=83所以商是20时，余数最大是83，此时除数是99-3=96。2003÷95=21……88+21×3=71所以商是21时，余数最大是71，此时除数是95-3=92。2003÷91=22……11+22×3=67所以商是22时，余数最大是67，此时除数是91-3=88。2003÷87=23……22+23×3=71所以商是23时，余数最大是71，此时除数是87-3=84。当除数小于84时，余数小于83。综上所述，余数最大是83，此时除数AB=96。

98、某服装厂要生产一批某种型号的学生服，已知每3米长的某种面料可做上衣2件。或做裤子3条，计划用300米长的这种布料生产学生服，应用多少米布料产生上衣，才能恰好配套?_____
A: 120B: 150C: 180D: 210
参考答案: C 本题解释:答案：C【解析】3米长可做上衣2件，或裤子3条，则300米布料可做上衣200件，或裤子300条，即如需成套，则上衣和裤子的数量必须同样多，那么上衣所用布料当为3/5，即180米，裤子为120米，共可做120套服装。所以答案为选项C。

99、分数4/9、17/35、101/203、3/7、151/301中最大的一个是_____。
A: 4/9B: 17/35C: 101/203D: 151/301
参考答案: D 本题解释:D【解析】首先目测可以知道3/7、17/35和101/203都小于1/2，而4/9和151/301都大于1/2，所以只要比较二者的大小就可以，通过计算，151/301大，所以选择D。

100、某数的百分之一等于0.003，那么该数的10倍是多少?_____。
A: 0.003B: 0.03C: 0.3D: 3
参考答案: D 本题解释:D【解析】某数的百分之一为0.003，则该数为0.3，那么它的10倍为3。故正确答案为D。