1、1996+1997+1998+1999+2000+2001等于_____。
A: 11986B: 11991C: 12987D: 12989
参考答案: B 本题解释: B 【解析】原式=（2000-4）+（2000-3）+（2000-2）+（2000-1）+（2000+1）=2000×6-4-3-2+1=12000-9=11991。

2、将1~9九个自然数分成三组，每组三个数，第一组三个数之积是48，第二组三个数之积是45，三组数字中数字之和最大是多少？_____
A: 15B: 17C: 18D: 20
参考答案: C 本题解释:【答案】C。解析：显然要对48和45进行乘法拆分，显然45的可拆分情况较少，故先拆分45＝1×5×9，由此可知48＝2×3×8＝2×4×6两种拆分情况，由此可知第三组三个数对应48的拆分也有两种情况：4、6、7；3、7、8。于是可知三组数字中加和最大的一组为3、7、8，加和为18。故正确答案为C。

3、有四个数，其中每三个数的和分别是45，46，49，52，那么这四个数中最小的一个数是多少？_____
A: 12B: 18C: 36D: 45
参考答案: A 本题解释:将45，46，49，52直接相加，可知其值等于原来四个数之和的3倍，于是可知原四个数字之和为（45+46+49+52）÷3=64，因此最小的数为64-52＝12。故选A。

4、32头牛和若干匹马的价钱相等，如果把牛的头数和马的头数互换，马的头数再减少14头，此时二者的价钱又相等了。请问，每头牛和马的价格比为多少?_____
A: 2：1B: 3：2C: 4：3D: 3：4
参考答案: D 本题解释:【答案】D。解析：设32头牛和x匹马的价钱相同，则交换后，x头牛和32-14=18头马的价钱相同，则32：x=x：18，解得x=24。故每头牛和马的价格比为24：32=3：4。

5、1～100各数所有不能被9整除的自然数的和是_____。
A: 217B: 594C: 5050D: 4456
参考答案: D 本题解释:D解析：在1至100中，被9整除的数的和是9+18+27+…+99=9×(1+2+3+…+11)=9×66=5941至100各数之和是1+2+3+…+100=100(1+100)2=5050所以在1至100的各数中，所有不能被9整除的数的和是5050-594=4456。因此，本题正确答案为D。

6、一桶农药，加入一定量的水稀释后，浓度为15%;再加入同样多的水稀释，农药的浓度变为12%，若第三次再加入同样多的水，农药的浓度将变为多少?_____
A: 8%B: 10%C: 11%D: 13%
参考答案: B 本题解释:B。【解析】设δ加水稀释前农药量为x,?次所加水量为a，所求浓度为y%，则(x+a)15%=(x+2a)12%=(x+3a)y%，解得y%=10%。

7、王家村西瓜大丰收后，全村男女老少分四个组品尝西瓜，且每组人正好一样，小伙子一个人吃1个，姑娘两个人吃1个，老人三个人吃1个，小孩四个人吃1个，一共吃了200个西瓜，问王家村品尝西瓜的共有_____
A: 368人B: 384人C: 392人D: 412人
参考答案: B 本题解释: B。方法一：利用整除关系。答案必须是2，3，4的公倍挚，也就是说答案必须是12的整数倍数。只有B满足。方法二：假设每组有x人。x+x/2+x/3+x/4=200，解得x=96，96×4=384(人)。

8、2007年4月20日，上证综指早盘高开11点，以3460.90点开盘后，随即逐波上扬，至终盘报收于3584.20点，较上一个交易日上涨了_____
A: 3.56%B: 11点 C: 113.70点 D: 134.30点
参考答案: D 本题解释: 【解析】较上一个交易日上涨多少应该以上个交易日收盘点数为准，所以高开的11点依然属于今天上涨的部分，故有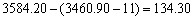点。故选D。

9、大小两个数的和是50.886，较大数的小数点向左移动一位就等于较小的数，求较大的数是_____。
A: 46.25　 B: 40.26 　C: 46.15　D: 46.26
参考答案: D 本题解释:【解析】D。 四个选项的小数点后都是两位，两数之和为50.886，则两个数的尾数都为6，所以可以排除A、C两项。将B、D两项代入，只有D项符合。

10、甲、乙沿同一公路相向而行，甲的速度是乙的1.5倍，已知甲上午8点经过邮局，乙上午10点经过邮局。问：甲乙在中途何时相遇？_____
A: 8点48分 B: 8点30分 C: 9点 D: 9点10分
参考答案: A 本题解释:A。【解析】设乙的速度为x，甲就是1.5x，当甲8点到邮局时，乙离邮局还有2个小时的路程（2x），甲乙走完2x路程需要2x/（1.5x+x）=4/5小时=48分钟，加上8点，就是8点48分相遇。

11、有一条400米长的环形跑道。甲、乙两人骑车从A点出发，背向而行。甲的初始速度为1米/秒，乙的初始速度为11米/秒。每当两人相遇。甲的速度就增加1米/秒。乙的速度减少1米/秒。那么当两人以相等的速度相遇时，距离A点多少米?_____
A: 50B: 60C: 75D: 100
参考答案: D 本题解释:D。此题为环形相遇问题，由于每次相遇路程相同，s=400米，速度和均为1+11=12米/秒，因此每次相遇时间都等于400÷12秒。两人速度相等时均为6米/秒，甲骑行总路程为400÷12×（1+2+3+4+5+6）=700米。400×2-700=100米，距离A点100米。

12、我们知道，一个正方形可以剪成4个小正方形，那么一个正方形能否剪成11个正方形，能否剪成13个正方形(大小不一定相同)？_____
A: 前者能，后者不能B: 前者不能，后者能C: 两个都能D: 两个都不能
参考答案: C 本题解释:【答案】C。

13、药厂使用电动研磨器将一批晒干的中药磨成药粉。厂长决定从上午10点开始，增加若干台手动研磨器进行辅助作业。他估算如果增加2台，可在晚上8点完成，如果增加8台，可在下午6点完成。问如果希望在下午3点完成，需要增加多少台手工研磨器？_____
A: 20B: 24C: 26D: 32
参考答案: C 本题解释:【答案】C。解析：设原有电动研磨器为N台，需要增X台手工研磨器，根据牛吃草公式有：Y=(N+2)10;Y=(N+8)8，解得N=22，Y=240;代入Y=(N+X)5解得X=26，故选择C选项。

14、4532×79÷158的值是_____。
A: 2266B: 2166C: 2366D: 2362
参考答案: A 本题解释:【答案】A。解析：4532×79÷158＝4532÷（158÷79）＝4532÷2＝2266。故正确答案为A。

15、篮球规则中得分有3分，2分，1分，若在一次比赛中，队员A一人得了13分，那么他的得分组合共_____种。
A: 18　B: 19　C: 20　D: 21
参考答案: D 本题解释:D[解析]当A的3分分别拿到4，3，2，1，0次的时候，对应的组合数分别是1，3，4，6，7，所以A的得分组合共有1+3+4+6+7=21种，选D。

16、两辆汽车同时从A、B两站相对开出，在B侧距中点20千米处两车相遇，继续以原速前进，到达对方出发站后又立即返回，两车再在距A站160千米处第二次相遇。求A、B两站距离是A_____。
A: 440千米B: 400千米C: 380千米D: 320千米
参考答案: A 本题解释:A[解析]首先，注意到第一次相遇后到第二次相遇时行的路程是出发到第一次相遇时行的路程的2倍。设A、B两站相距x千米，则第一次相遇时，B车行了（0.5x-20）千米;第二次相遇时，B车共行了（0.5x-20）×3（千米），或一个全长又160千米。列方程，得：（0.5x-20）×3=x+160x=440因此，本题正确答案为A。

17、货车和客车分别由甲乙两地相对开出，在货车离甲地30公里处与客车相遇，相遇后两车继续前进，分别到达甲乙两地后立即返回，途中在离乙地21公里处，货车又与客车相遇。问甲乙两地的距离是多少公里？_____
A: 39B: 69C: 81D: 111
参考答案: B 本题解释:B。货车和客车第一次相遇时，共行了一个全程，其中货车行了30公里。第二次相遇时，两车共行了三个全程，那么货车应当是行了30×3=90（公里）。这90公里恰好等于一个全程加上此时货车距离乙地的距离，所以甲乙两地的距离为90一21=69（公里）。

18、某小学五年级同学分成69个小组，每组3人，去参加植树劳动。在这些小组中，只有1名男同学的共有15个小组，至少有2名女同学的共有36个小组，有3名男同学的小组与有3名女同学的小组同样多。问这所小学五年级共有男同学多少名?_____
A: 102B: 136C: 144D: 158
参考答案: A 本题解释:【解析】A。有1名男生2名女生的小组有15个，则有3名女生的小组有36-15=21个，所以有3名男生的小组也有21个，只有1名女生的小组有69-15-21-21=12个，故男生一共有15+12×2+21×3=102名。

19、孙某共用24000元买进甲、乙股票若干，在甲股票升值15%、乙股票下跌10%时全部抛出，共赚到1350元，则孙某最初购买甲、乙两支股票的投资比例是_____。
A: 5∶3 B: 8∶5 C: 8∶3 D: 3∶5
参考答案: A 本题解释:A。经济利润问题。设甲股票买了X元，乙股票买了Y元，列方程组：X+Y=2400015%X-10%Y=1350解得X=15000，Y=9000，故X∶Y=15∶9=5∶3, 选A。

20、一艘游轮逆流而行，从A地到B地需6天;顺流而行，从B地到A地需4天。问若不考虑其他因素，一块塑料漂浮物从B地漂流到A地需要多少天_____
A: 12天B: 16天C: 18天D: 24天
参考答案: D 本题解释:D【解析】设静水速度是X，水流速度是Y，那么可以列出方程组：1/（X-Y）=6，1/（X+Y）=4;可解得1/Y=24，即为水流速度漂到的时间。

21、如图所示，半圆与等腰三角形ABC的斜边AC相切，AB=BC=1。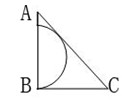问半圆的直径是多少?_____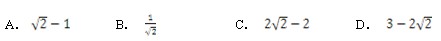
A: AB: BC: CD: D
参考答案: C 本题解释:C

22、某人在公共汽车上发现一个小偷向相反方向步行，10秒钟后他下车去追小偷，如果他的速度比小偷快一倍，而汽车的速度是他速度的5倍，则此人追上小偷需要_____
A: 20秒B: 50秒C: 95秒D: 110秒
参考答案: D 本题解释:【解析】D。设小偷速度为V，则他的速度2V，汽车的速度10V。l0秒内小偷走了10V，但车子走了100V，所以距离是110V，而他和小偷的速度差为V，即追上小偷需要110秒。

23、某人在公共汽车上发现一个小偷向相反方向步行，10秒钟后他下车去追小偷，如果他的速度比小偷快一倍，比汽车慢4/5，则此人追上小偷需要_____。
A: 20秒B: 50秒C: 95秒D: 110秒
参考答案: D 本题解释:答案：D【解析】设某人速度为v，则小偷速为0.5v，汽车速为5v，10秒钟内，与小偷相差（0.5+5）v×10=55v，追求时速差为0.5v，所以所需时间为110秒。

24、某服装厂要生产一批某种型号的学生服，已知每3米长的某种面料可做上衣2件。或做裤子3条，计划用300米长的这种布料生产学生服，应用多少米布料产生上衣，才能恰好配套?_____
A: 120B: 150C: 180D: 210
参考答案: C 本题解释:答案：C【解析】3米长可做上衣2件，或裤子3条，则300米布料可做上衣200件，或裤子300条，即如需成套，则上衣和裤子的数量必须同样多，那么上衣所用布料当为3/5，即180米，裤子为120米，共可做120套服装。所以答案为选项C。

25、某年级有4个班，不算甲班其余三个班的总人数有131人，不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少1人，问这四个班共有多少人? _____
A: 177B: 176C: 266D: 265
参考答案: A 本题解释:A。【解析】有①乙+丙+丁=131，②甲+乙+丙=134，③乙+丙+1=甲+丁，①-③得丁-1=131-甲-丁，甲=132-2丁，①-②得，甲=丁+3，丁=43，总人数为134+43=177人

26、数字3、5至少都出现一次的三位数有多少个？_____
A: 48B: 52C: 54D: 60
参考答案: B 本题解释:【答案】B。解析：

27、某班有50位同学参加期末考试，结果英文不及格的有15人，数学不及格的有19人，英文和数学都及格的有21人。那么英文和数学都不及格的有_____人。
A: 4B: 5C: 13D: 17
参考答案: B 本题解释:本题正确答案为B。解析：设英文和数学都不及格的有x人，由容斥原理可得15+19-x=50-21，得x=5,故选B。

28、数学竞赛，共25道题目，评分标准是每做对一题得5分，做错一题倒扣3分，没做为0分，某学生得了94分，则他做错了多少道题? _____
A: 2B: 3C: 4D: 5
参考答案: A 本题解释:A。如果全做对，应得125分。现在少得了125-94=31分，答错一道减少5+3=8分，不答一道减少5分，8×2+5×3=31分，故他做错了2道题。

29、A、B两地以一条公路相连。甲车从A地，乙车从B地以不同的速度沿公路匀速率相向开出。两车相遇后分别掉头，并以对方的速率行进。甲车返回A地后又一次掉头以同样的速率沿公路向B地开动。最后甲、乙两车同时到达B地。如果最开始时甲车的速率为X米/秒，则最开始时乙车的速率为（）。
A: 4X米/秒B: 2X米/秒C: 0.5X米/秒D: 无法判断
参考答案: B 本题解释:答案：B。显然最初乙的速度较快，由题意知，以甲车的速率走完了一遍全程，以乙车的速率走了两遍全程，所费时间相等，故乙车速度为甲车两倍。

30、商场的自动扶梯以匀速由下往上行驶，两个孩子嫌扶梯走得太慢，于是在行驶的扶梯上，男孩每秒钟向上走2个梯级，女孩每2秒钟向上走3个梯级。结果男孩用40秒钟到达，女孩用50秒钟到达。则当该扶梯静止时，可看到的扶梯梯级有_____。
A: 80级B: 100级C: 120级D: 140级
参考答案: B 本题解释:B。【解析】男孩所走的台阶数为40×2=80，女孩所走的台阶数为50/2×3=75，那么电梯的速度就应该为（80-75）/（50-40）=0.5，电梯所经过的台阶就为40×0.5=20， 电梯经过的台阶加上男孩经过的台阶，就是电梯的台阶数，即100级。

31、如是2003除以一个两位数后，所得余数最大，则这个两位数为_____。
A: 92B: 82C: 88D: 96
参考答案: D 本题解释:D【解析】 2003÷99=20……2323+20×3=83所以商是20时，余数最大是83，此时除数是99-3=96。2003÷95=21……88+21×3=71所以商是21时，余数最大是71，此时除数是95-3=92。2003÷91=22……11+22×3=67所以商是22时，余数最大是67，此时除数是91-3=88。2003÷87=23……22+23×3=71所以商是23时，余数最大是71，此时除数是87-3=84。当除数小于84时，余数小于83。综上所述，余数最大是83，此时除数AB=96。

32、某单位举行“庆祝建党90周年”知识抢答赛，总共50道抢答题。比赛规定：答对1题得3分，答错1题扣1分，不抢答得0分。小军在比赛中抢答了20道题，要使最后得分不少于50分，则小军至少要答对_____道题。
A: 16B: 17C: 18D: 19
参考答案: C 本题解释:假设答对2题，取最坏情形，剩下都答错，则答错20—x题，总分不少于50则有3x-（20-z）≥50，求得x≥17.5，取最小值为18。

33、电影票10元一张，降价后观众增加一倍，收入增加1/5，则一张票降价多少元?_____
A: 8B: 6C: 4D: 2
参考答案: C 本题解释:答案：C。代入法。10元一张票，一个人去看，总收入10元，降价了以后， 观众增加了1倍，2个人去看，收入增加了1/5，也就是说，两个人看收入为12元，每张票价就是6元钱，相比原来的10元钱一张，下降了4元，所以答案是C

34、小明和小强从400米环形跑道的同一点出发，背向而行。当他们第一次相遇时，小明转身往回跑;再次相遇时，小强转身往回跑;以后的每次相遇分别是小明和小强两人交替调转方向。小明每秒跑3米，小强每秒跑5米，则在两人第30次相遇时，小明共跑了多少米?
A: 11250B: 13550C: 10050D: 12220
参考答案: A 本题解释:【答案】A。

35、2007年4月20日，上证综指早盘高开11点，以3460.90点开盘后，随即逐波上扬，至终盘报收于3584.20点，较上一个交易日上涨了_____
A: 3.56% B: 11点 C: 113.70点 D: 134.30点
参考答案: D 本题解释: 【解析】较上一个交易日上涨多少应该以上个交易日收盘点数为准，所以高开的11点依然属于今天上涨的部分，故有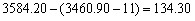点。故选D。

36、一个正方体木块放在桌子上，每一面都有一个数，位于相对面两个数的和都等于13，小张能看到顶面和两个侧面，看到的三个数和为18；小李能看到顶面和另外两个侧面，看到的三个数的和为24，那么贴着桌子的这一面的数是多少？_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:B。题目给出相对面数字之和为13的条件，则注意将其余条件中出现的相对面合在一起。从这一点出发，可以看出若将小张与小王看到的面合在一起，则实际共看到2个顶面与4个不同的侧面。而四个不同侧面恰为两组对面，也即其数字之和为13×2=26，因此顶面的数字为（18+24—26）÷2=8，于是底面数字为13—8=5。故选B。

37、4只小鸟飞入4个不同的笼子里去，每只小鸟都有自己的一个笼子(不同的鸟，笼子也不相同)，每个笼子只能飞进一只鸟。若都不飞进自己的笼子里去，有多少种不同的飞法?_____。
A: 7B: 8C: 9D: 10
参考答案: C 本题解释:C。本题属于计数问题。本题是排列组合中的错位问题，根据对错位问题数字的记忆，答案应为9种。所以选择C选项。计算过程：设四只小鸟为1，2，3，4，则1有3个笼可选择，不妨假设1进了2号笼，则2也有3个笼可选择，不妨设2进了3号笼，则剩下鸟3、4和笼1、4只有一种选择。所以一共有3×3=9种。

38、某人在雅虎上申请了一个邮箱，邮箱密码是由0至9中任意4个数字组成，他任意输入4个数字，输入正确密码的概率是_____。
A: 10　B: 10　C: 10　D: 10
参考答案: B 本题解释:B[解析]正确的密码只有一个，这10个数字的组合共有10个，所以答案是B。

39、一本100多页的书，被人撕掉了4张.剩下的页码总和为8037。则该书最多有多少页_____
A: 134B: 136C: 138D: 140
参考答案: A 本题解释:【答案】A。解析：撕掉四张纸的页码数之和是偶数，由剩下页码数是奇数可知总的页码数是奇数，排除B、D。若为C，则撕掉的页码数之和是138×（138+1）÷2—8037=1554>138×8，矛盾。A项符合题意。

40、某校人数是一个三位数，平均每个班级36人，若将全校人数的百位数与十位数对调，则全校人数比实际少180人，那么原校人数最多可以达到多少人：_____
A: 900B: 936 C: 972D: 990
参考答案: C 本题解释:C。【解析】根据能被36整除和百位十位对调后相差180两个条件，用代入法可很快求得。

41、有苹果，桔子各一筐，苹果有240个，桔子有313个，把这两筐水果平均分给一些小朋友，已知苹果分到最后余2个，桔子分到最后还余7个，求最多有多少个小朋友参加分水果？_____
A: 14 B: 17 C: 28 D: 34
参考答案: D 本题解释:【答案】D。解析：240-2=238，313-7=306，此题即要求238和306的最大公约数，238=2×7×17、306=2×3×3×17，可知最大公约数是34。

42、四个连续自然数的积为3024，它们的和为_____
A: 26B: 52C: 30D: 28
参考答案: C 本题解释:【解析】C。因式分解得，原式＝33×24×7，可知这几个自然数是6、7、8、9。

43、纸上写着2、4、6三个整数，改变其中任意一个，将它改写成为其他两数之和减1，这样继续下去，最后可以得到的是_____。
A: 595、228、368B: 44、95、50C: 103、109、211D: 159、321、163
参考答案: A 本题解释:A。

44、某计算机厂要在规定的时间内生产一批计算机，如果每天生产140台，可以提前3天完成;如果每天生产120台，就要再生产3天才能完成。问规定完成的时间是多少天?_____
A: 30B: 33C: 36D: 39
参考答案: D 本题解释:答案：D【解析】解答此题可以同时使用代入法和方程法。为快速解题可首先考虑方程法，设规定时间为x天，则（x-3）×l40=（x+3）×l20，解得x=39。故选D。

45、一列客车长250米，一列货车长350米，在平行的轨道上相向行驶，从两车头相遇到两车尾相离经过15秒，已知客车与货车的速度比是5∶3。问两车的速度相差多少?_____
A: 10米/秒B: 15米/秒C: 25米/秒D: 30米/秒
参考答案: A 本题解释:【答案解析】根据题意可知，两车的速度和为(250+350)÷15=40米/秒，且两车的速度比是5∶3，则两车的速度差为10米/秒。

46、三边长均为整数且最大边长为2009的三角形共有多少个？_____
A: 1008016 B: 1009020 C: 1010025 D: 2019045
参考答案: C 本题解释: C。根据三角形的构成原理，可知最大边长为2009时，另两边的和大于2009，差小于2009，则两边≤2009且≥1，则可知介于最长边与最短边之间的那条中边的长度必≥1005且≤2009。中边为1005时，另一边=1 005，1种可能；中边为1006时，另一边=1004，1005，1006，共3种可能；中边为1007时，另一边=1003，1004，1005，1006，1007，共5种可能；……中边为2009时，另一边=1~2009，共2009种可能。因此三角形总和=1+3+5+…+2007+2009=1005（1+2009）/2=1010025种。所以答案为C项。

47、某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训? _____
A: 8B: 10C: 12D: 15
参考答案: D 本题解释:【解析】D。本题可直接看出答案，乙教室一次45人，共有1290人，所以乙次数一定为偶数，又因为一共27次，所以甲一定为奇数，直接选15。

48、在一条公路旁有4个工厂，每个工厂的人数如图所示，且每两厂之间距离相等。现在要在公路旁设一个车站，使4个工厂的所有人员步行到车站总路程最少，这个车站应设在几号工厂门口?_____
A: 1号B: 2号C: 3号D: 4号
参考答案: C 本题解释:C【解析】 一般情况车站设在几个工厂的中间，即设在2号工厂或3号工厂门口。由于各厂人数不同，还是应通过计算再决定车站在哪一个工厂门口合适。如果设车站建在2号工厂门口，且设每两个工厂之间距离为1千米，那么4个工厂所有人员步行总路程为：1×100+1×80+2×215=100+80+430=610（千米）如果车站设在3号工厂门口，每两个工厂之间的距离为1千米，那么4个工厂所有人员步行总路程为：1×100×2+1×120+1×215=200+120+215=535（千米）显然，车站设在3号厂门口，才能使4个工厂所有人员步行到车站总路程最少。故本题选C。

49、将半径分别为4厘米和3厘米的两个半圆如图放置，则阴影部分的周长是_____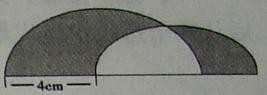
A: 21.98厘米 B: 27.98厘米 C: 25.98厘米 D: 31.98厘米
参考答案: B 本题解释: 【解析】B。先算出两个半圆的周长是πr=3.144+3.143=21.98，剩下两边的长度，已知一条为4厘米，另一条为=（4+6）-8=2，所以阴影部分的周长=2+4+21.98=27.98。

50、2004×(2.3×47+2.4)÷(2.4×47-2.3)的值为_____。
A: 2003B: 2004C: 2005D: 2006
参考答案: B 本题解释:答案：B

51、某村有甲乙两个生产小组，总共50人，其中青年人共13人。甲组中青年人与老年人的比例是2∶3，乙组中青年人与老年人的比例是1∶5，甲组中青年人的人数是：_____
A: 5人B: 6人C: 8人D: 12人
参考答案: C 本题解释:【答案】C。解析：设甲组人数为5x,乙组人数为6y。有，解得x=4。因此甲组青年人的人数为8。

52、两个相同的瓶子装满酒精溶液，一个瓶子中酒精与水的体积比是3:1，另一个瓶子中酒精与水的体积比是4:1，若把两瓶酒精溶液混合，则混合后的酒精和水的体积之比是多少?_____
A: 31:9B: 7:2C: 31:40D: 20:11
参考答案: A 本题解释:【答案解析】(3/4+4/5)/(1/4+1/5)=31：9

53、有一只怪钟，每昼夜设计成10小时，每小时100分钟，当这只怪钟显示5点时，实际上是中午12点。当这只怪钟显示8点50分时，实际上是什么时间? _____
A: 17点50分B: 18点10分C: 20点O4分D: 20点24分
参考答案: D 本题解释:D。怪钟时间从5点走到8点50分的3个小时50分钟，相当于标准时间一天的35%，即24×0.35=8.4小时。因此实际时间为12+8.4=20.4时，即20点24分。

54、杂货店分三次进了一些货物，已知每一次的进货单价都是上一次的80%，且第一次的进货单价为5元。已知这些货物恰好能够排成一个三层的空心方阵，且最内层、中间层和最外层恰好分别是第一、二、三次所进的货物，且最外层每边有7个货物。现要保证20%利润率的情况下，杂货店应该将货物至少定为多少元?_____
A: 3.90B: 4.12C: 4.36D: 4.52
参考答案: D 本题解释:【解析】D。三次的单价分别为5元、5×80%=4元、4×80%=3.2元。最外层有货物(7-1)x4=24个，中间层有24-8=16个，最内层有I6-8=8个。所以总进价为3.2x24+4xl6+5x8=l80.8元，要保证20%的利润率，货物定价为180.8x(1+20%)÷(24+16+8)=4.52元。

55、A、B、C、D、E，5个小组开展扑克牌比赛，每两个小组之间都要比赛一场，到现在为止，A组已经比赛了4场，B组已经比赛了3场，C组已经比赛了2场，D组已经比赛了1场，问E组已经比赛了几场（）
A: oB: 1C: 2D: 3
参考答案: C 本题解释:C【解析】A组已经比赛了4场，说明A组与B、C、D、E这4个组都进行过比赛;D组已经比赛了1场，则根据上一个条件，D组只与A组进行过比赛;B组已经比赛了3场，则根据上一个条件，B组只与A、C、E组进行过比赛;C组已经比赛了2场，则根据上面的条件，C组只能与A、B组进行过比赛;所以E组与A、B组进行过比赛。

56、如果某商店 以每打1.8元的价格购进6打小工艺品(每打12件).之后又以每件0.2元卖出.这些小商品全部卖完后商店可得多少利润？_____
A: 32元 B: 3.6元 C: 2.4元 D: 2.84元
参考答案: B 本题解释:B【解析】0.2×12×6-1.8×6=3.6，一打=12个。

57、某船第一次顺流航行21千米又逆流航行4千米，第二次在同一河道中顺流航行12千米，逆流航行7千米，结果两次所用的时间相等。则顺水船速与逆水船速之比是_____。(设船本身的速度及水流的速度都是不变的)
A: 4∶1B: 3∶1C: 2∶1D: 9∶1
参考答案: B 本题解释:B 【解析】船第一次顺流航行21千米，第二次顺流航行12千米，21-12=9，也就是第一次顺流多用了航行9千米所用的时间，第二次逆流比第一次多用时间于3千米的航行上，总的两次时间相等。就是顺流9千米用的时间等于逆流3千米所用的时间。顺流船速：逆流船速=（21-12）∶（7-4）=3∶1，即顺水船速是逆水船速的3倍。

58、从某车站以加速度为1/18米/秒2始发的甲列车出发后9分钟，恰好有一列与甲列车同方向，并以50米/秒作匀速运行的乙车通过该车站，则乙车运行多少分钟与甲车距离为最近？_____
A: 9B: 3C: 5D: 6
参考答案: D 本题解释:D。当甲车速度小于乙车时，乙车逐渐缩短与甲车的距离；当甲车速度大于乙车时，两车之间距离拉大；仅当两车速度相同时，两车距离最小。根据Vt=Vo+at，可得50=1/18×9×60+1/18×t，求得t=360秒=6分钟。

59、某市出租车运费计算方式如下：起步价2公里6元，2公里之后每增加1公里收费1.7元，6公里之后每增加1公里收费2.0元，不足1元按四舍五入计算。某乘客乘坐了31公里，应该付多少元车费？ _____
A: 63 B: 64 C: 65 D: 66
参考答案: A 本题解释:A。2公里以内收费6元；2－6公里收费1.7×4＝6.8元；6－31公里收费2×25＝50元。因此总计应付车费62.8元，四舍五入即63元。故选A项。

60、在一次国际美食大赛中，中、法、日、俄四国的评委对一道菜品进行打分。中国评委和法国评委给出的平均分是94，法国评委和日本评委给出的平均分是90，日本评委和俄国评委给出的平均分是92，那么中国评委和俄国评委给出的平均分是_____。
A: 93分B: 94分C: 96分D: 98分
参考答案: C 本题解释:C 解析：设中、法、日、俄四国的评委给出的分数分别是A、B、C、D，根据题意可知：A+B=94×2，B+C=90×2，C+D=92×2，又因为A+D=（A+B）+（C+D）-（B+C）=94×2+92×2-90×2=（94+92-90）×2=96×2所以中国评委和俄国评委给出的平均分是96分，本题正确答案为C。

61、下列哪项能被11整除? _____
A: 937845678B: 235789453C: 436728839D: 867392267
参考答案: A 本题解释:A【解析】9+7+4+6+8=343+8+5+7=2334-23=11所以，答案是A。

62、有100人参加运动会的三个比赛项目，每人至少参加一项，其中未参加跳远的有50人，未参加跳高的有60人，未参加赛跑的有70人。问至少有多少人参加了不止一个项目？_____
A: 7B: 10C: 15D: 20
参考答案: B 本题解释:【解析】B。最值问题。由题意，参加跳远的人数为50人，参加跳高的为40人，参加赛跑的为30人；即参加项目的人次为120人次；故欲使参加不止一项的人数最少，则需要使只参加一项的人数最多为x，参加3项的人数为y；故x+3y=120，x+y=100，解得y=10。

63、

64、小刚骑自行车从8路汽车起点出发，沿8路车的行驶路线前进。当他骑了1650米时，一辆8路公共汽车从起点站出发，每分钟行驶450米。这辆汽车在行驶过程中每行5分钟停靠一站，停靠时间为1分钟。已知小刚骑车的速度是汽车行驶速度的，这辆汽车出发后多长时间追上小刚?_____
A: 15分钟B: 16分钟C: 17分钟D: 18分钟
参考答案: C 本题解释:【解析】C。如果不休息的话汽车要1650÷（450-450×）=11分钟，11÷5=2……1，则汽车在追上小刚前休息了2分钟，而这两分钟内，小刚又走了450××2=600米，汽车又要用600÷（450-450×）=4分钟，故一共用了11+4+2=17分钟。

65、3×999+8×99+4×9+15的值是_____。
A: 3866 B: 3855 C: 3840 D: 3877
参考答案: C 本题解释:C。原式转化为3×（1000-1）+×8×（100-1）+4×（10-1）+15=3000-3+800-8+40-4+15=3000+800+40-15+15=3840，所以正确答案为C项。

66、一只船沿河顺水而行的航速为30千米/小时，已知按同样的航速在该河上顺水航行3小时和逆水航行5小时的航程相等，则此船在该河上顺水漂流半小时的航程为：_____
A: 1千米B: 2千米C: 3千米D: 6千米
参考答案: C 本题解释:【答案解析】根据水速=(顺速-逆速)/2，所以(30-18)/2=6，因此漂流半小时就是6×1/2=3，选C。

67、有黑、白、黄色袜子各10只，不用眼睛看，任意地取出袜子来，使得至少有两双袜子不同色，那么至少要取出_____只袜子。
A: 12B: 13C: 11D: 14
参考答案: B 本题解释:【解析】考虑最坏的情形，把某一种颜色的袜子全部先取出，然后，在剩下两色袜子中各取出一只，这时再任意取一只都必将有两双袜子不同色，即10+2+l=13（只）。故选B。

68、小陈、小张、小赵和小周四个人的平均基本工资为1010元，这次工资调整，他们基本工资分别上调了254元、191元、146元和209元，现在四个人的平均基本工资是_____
A: 1180元B: 1210元C: 1080元D: 1220元
参考答案: B 本题解释: 【解析】B。现在平均基础工资为1010+（254+191+146+209）÷4=1210元。

69、0， 1， 1， 1， 2， 2， 3， 4八个数字做成的八位数，共可做成______个。_____
A: 2940B: 3040C: 3142D: 3144
参考答案: A 本题解释:A【解析】不妨先把这8个数字看作互不相同的数字，0暂时也不考虑是否能够放在最高位，那么这组数字的排列就是P（8，8），但是，事实上里面有3个1，和2个2，3个1在P（8，8）中是把它作为不同的数字排列的，那就必须从P（8，8）中扣除3个1的全排列P（3，3），因为全排列是分步完成的，在排列组合中，分步相乘，分类相加。可见必须通过除掉P（3，3）才能去掉这部分重复的数字形成的重复排列。2个2当然也是如此，所以不考虑0作为首位的情况是 P88/（P33×P22）。现在再来单独考虑0作为最高位的情况有多少种：P77/（P33×P22），最后结果就是：P88/（P33×P22）-P77/（P33×P22）=2940。

70、一个质数的3倍与另一个质数的2倍之和等于20，那么这两个质数的和是_____。
A: 8 　 B: 9 　 C: 7 　 　D: 6
参考答案: B 本题解释:【解析】B。 设这两个质数分别为x、y,则3x+2y=20。2y和20都是偶数，则3x也是偶数，即x为偶数。又因为x同时是质数，则x=2，y=7。两质数之和x+y=9。故选B。

71、杂货店分三次进了一些货物，已知每一次的进货单价都是上一次的80%，且第一次的进货单价为5元。已知这些货物恰好能够排成一个三层的空心方阵，且最内层、中间层和最外层恰好分别是第一、二、三次所进的货物，且最外层每边有7个货物。现要保证20%利润率的情况下，杂货店应该将货物至少定为多少元？_____
A: 3.90 B: 4.12 C: 4.36 D: 4.52
参考答案: D 本题解释:【答案】D。解析：三次的单价分别为5、5×80%=4、4×80%=3.2元。最外层有货物（7-1）×4=24个，中间层有24-8=16个，最内层有16-8=8个。所以总进价为3.2×24+4×16+5×8=180.8元，要保证20%的利润率，货物定价为180.8×（1+20%）÷（24+16+8）=4.52元。

72、阳光下，电线杆的影子投射在墙面及地面上，其中墙面部分的高度为1米，地面部分的长度为7米。甲某身高1.8米，同一时刻在地面形成的影子长0.9米。则该电线杆的高度为_____。
A: 12米B: 14米C: 15米D: 16米
参考答案: C 本题解释:【答案】C。解析：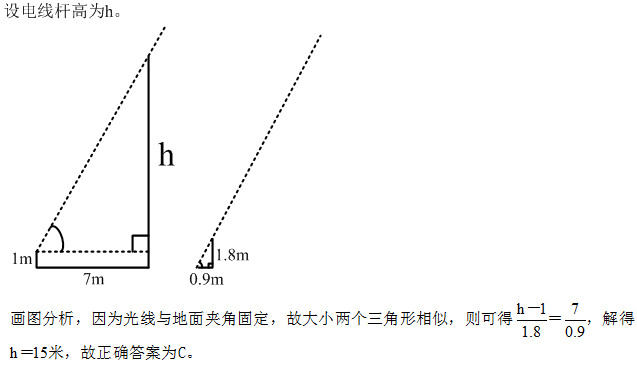

73、甲、乙、丙三队要完成A，B两项工程，B工程工作量比A工程的工作量多1/4 ，甲、乙、丙三队单独完成A工程所需时间分别是20天、24天、30天。为了同时完成这两项工程，先派甲队做A工程，乙、丙两队共同做B工程，经过几天后，又调丙队与甲队共同完成A工程，那么，丙队甲队合做了多少天? _____
A: 18B: 15C: 10D: 3
参考答案: D 本题解释:【解析】D。解析：三队完成这项工程一共用了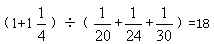天，乙队一直在做B工程，一共做了 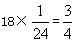，则B工程剩下的 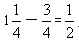为丙做的，故丙队与乙队合做了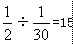天，与甲队合做了18-15=3天。

74、在1至1000的1000个自然数中，既不是4的倍数，也不是6的倍数的数共有多少个?_____
A: 375B: 416C: 625D: 791
参考答案: C 本题解释:C【解析】1000÷4=250（个），所以1至1000中4的倍数的数有250个。1000÷6=166……4，所以1至1000中6的倍数的数有166个。1000÷（4×6）=41……16，说明1至1000中既是4的倍数，又是6的倍数的数有41个。即4的倍数的个数与6的倍数的个数的交集有41个，如图所示。所以1至1000中，既是4的倍数，也是6的倍数的数共有209+125+41=375（个）。则1至1000中，既不是4的倍数，也不是6的倍数的数共有：1000-（209+125+41）=1000-375=625（个）。故本题选C。

75、一个数能被3、5、7整除，若用11去除这个数则余1，这个数最小是多少?_____
A: 105B: 210C: 265D: 375
参考答案: B 本题解释:B。这个数能被3、5、7整除，因此这个数是105的倍数.若这个数是105，105除以11的余数是6，不符合题意；若这个数是105×2＝210，210除以11的余数是1，满足题意。因此这个数最小是210。

76、小王的手机通讯录上有一手机号码，只记下前面8个数字为15903428。但他肯定，后面3个数字全是偶数，最后一个数字是6，且后3个数字中相邻数字不相同，请问该手机号码有多少种可能？_____
A: 15B: 16C: 20D: 18
参考答案: B 本题解释:后三位全是偶数，且三数中相邻数字不同，已知最后一位是6，所以倒数第二位有0、2、4、8四种可能，倒数第三位也有四种可能性，故该手机号码有4×4=16（种）可能。

77、20＋19－18－17＋16＋15－14－13＋12＋11···＋4＋3－2－1＝_____。
A: 10B: 15C: 19D: 20
参考答案: D 本题解释:【答案】D。解析：解析1：原式＝（20－18）＋（19－17）＋（16－14）＋（15－13）＋···＋（4－2）＋（3－1）＝2＋2＋2＋2＋···＋2＋2＝2×10＝20。故正确答案为D。解析2：原式＝20＋（19－18－17＋16）＋（15－14－13＋12）＋…＋（3－2－1）＝20。故正确答案为D。

78、有11个人围成一个圆圈，依次编成1—11号，从1号起轮流表演节目，轮流的方法是：隔一个人表演一个节目，隔两个人表演一个节目，再隔一个人表演一个节目，隔两个人表演一个节目……这样轮流下去，至少要表演多少个节目，才能使每个人表演的次数同样?_____
A: 22B: 24C: 25D: 28
参考答案: A 本题解释:A【解析】本题考查的是周期问题。表演的人数共11人，且每个人表演次数相同，则至少要表演11N个节目。符合条件的只有A。

79、将所有自然数,自1开始依次写下去得到:12345678910111213……,试确定第206788个位置上出现的数字_____。
A: 3B: 0C: 7D: 4
参考答案: C 本题解释:【答案】C。解析:一位数占l×9=9个位置,二位数占2×90=180个位置,三位数占3×900=2700个位置,四位数占4×9000=36000个位置,还剩:206788-9-180-2700-36000=167899,167899÷5=33579……4,所以答案为33579+10000=43579的第4个数字7。故应选C。

80、商店里有六箱货物，分别重15、16、18、19、20、31千克，两个顾客买走了其中五箱。已知一个顾客买的货物重量是另一个顾客的2倍。商店剩下的一箱货物重多少千克？_____。
A: 16 B: 18C: 19 D: 20
参考答案: D 本题解释:D 【解析】根据题意知道，货物的总重量是3个倍数，则它们的数字之和必定能被3整除，经过计算转换得知，剩下的那一箱重20千克。故选D。

81、妈妈给了红红一些钱去买贺年卡，有甲、乙、丙三种贺年卡，甲种卡每张0. 50元，丙种卡每张1. 20元。用这些钱买甲种卡要比买乙种卡多买8张，买乙种卡要比买丙种卡多买6张。妈妈给了红红多少钱?_____
A: 8元B: 10元C: 12元D: 15元
参考答案: C 本题解释: C解析：盈亏总额为0. 5×8+1. 2×6=11. 2（元），单价相差1. 2-0. 5=0. 7（元），所以共可买乙种卡11. 2÷0. 7=16（张）。妈妈给了红红0. 5×（16+8）=12（元）。故本题正确答案为C。

82、一瓶挥发性药物，每天挥发5毫升，15天后挥发了全部的75%，假如每天挥发的速度不变，余下的几天能挥发完?_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:B【解析】5×15÷75%=100ml这瓶药物共100ml，100-5×15=25ml，剩下25ml，25÷5=5天。

83、某店原来将一批苹果按100%的利润(即利润是成本的100%)定价出售，由于定价过高，无人购买，后来不得不按38%的利润重新定价，这样出售了其中的40%。此时，因害怕剩余水果腐烂变质，不得不再次降价，售出了剩余的全部水果。结果，实际获得的总利润是原定利润的30.2%，那么第二次降价后的价格是原定价的_____。
A: 75%B: 50.%C: 62.5%D: 45%
参考答案: C

84、100张多米诺骨牌整齐地排成一列，依顺序编号为1、2、3……99，100.第一次拿走所有奇数位置上的骨牌，第二次再从剩余骨牌中拿走所有奇数位置上的骨牌，依此类推。请问最后剩下的一张骨牌的编号是多少？_____
A: 32 B: 64 C: 88 D: 96
参考答案: B 本题解释:【解析】本题关键是理解题意，第一次拿走的是所有奇数，第二次拿走的各项是2分别乘以1、3、5、7、9……，依次类推，每拿走一次后，剩下的第一个数是20、21，22、23、24……，在100之内要使2n取值最大，所以最后剩下的是64，选B.

85、科学家进行一项实验，每隔五小时做一次记录。已知做第十二次记录时，挂钟的时针恰好指向9，那么第一次记录时，时针指向_____。 B: 1C: 2D: 3
参考答案: C 本题解释:【答案】C。解析：做第十二次记录时，离第一次记录共有55小时，即时针转4圈又7小时后时针指向9，那么开始时时针指向2，因此，本题答案为C。

86、一个两位数除以一个一位数，商仍是两位数，余数是8。问：被除数、除数、商以及余数之和是多少?_____
A: 98B: 107C: 114D: 125
参考答案: D 本题解释:【答案】D。解析：猜证结合的98÷10=9余8，10+98+9+8=125。

87、一间长250米、宽10米、高4米的仓库放置了1000个棱长为1米的正方体箱子，剩余的空间为_____立方米。 B: 1500C: 5000D: 9000
参考答案: D 本题解释:【答案】D。解析：仓库的容量为250×10×4＝10000立方米，1000个棱长为1米的正方体箱子体积为1000×1×1×1＝1000立方米，则剩余空间为10000－1000＝9000平方米，故正确答案为D。

88、地球表面的陆地面积和海洋面积之比是29︰71，其中陆地的四分之三在北半球，那么南、北半球海洋面积之比是_____
A: 284︰29B: 113︰55C: 371︰313D: 171︰113
参考答案: D 本题解释:【解析】D。根据题干中的比例关系，可以推断出南、北半球的海洋面积之比为：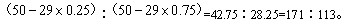

89、某A、B、C三地的地图如下图所示，其中A在C正北，B在C正东，连线处为道路。如要从A地到达B地，且途中只能向南、东和东南方向行进，有多少种不同的走法（）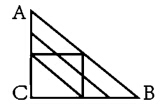
A: 9B: 11C: 13D: 15
参考答案: D 本题解释:【答案】D。解析：从A点出发从上向下总共4个路口，按照题目要求，第一个路口到B地有3种走法；第二个路口在第一个路口路线基础上加了2种走法，共5种走法；第三个路口在第二个路口路线的基础上又加了一条路线，共6种走法；最后一个路口只有一个走法。所有总计15种走法。

90、甲、乙两地相距100千米，张先骑摩托车从甲出发，1小时后李驾驶汽车从甲出发，两人同时到达乙地。摩托车开始速度是50千米/小时，中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟，那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 3/2C: 1/3D: 2
参考答案: C 本题解释:C解析：汽车行驶100千米需100÷80=5/4(小时)，所以摩托车行驶了5/4+1+1/6=29/12(小时)。如果摩托车一直以40千米/小时的速度行驶，29/12小时可行驶96(2/3)千米，与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷(50-40)=1/3(小时)。故本题选C.

91、小王练习射击，每次10发。练了若干次之后，小王准备再打一次。如果这次小王打48环，那么平均每次打56环。如果最后这次打68环，那么平均每次打60环。小王共练习了多少次_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:【答案】B。解析：平均数问题，(68-48)÷(60-56)=5。

92、某计算机厂要在规定的时间内生产一批计算机，如果每天生产140台，可以提前3天完成;如果每天生产120台，就要再生产3天才能完成。问规定完成的时间是多少天?_____
A: 30B: 33C: 36D: 39
参考答案: D 本题解释:答案：D【解析】解答此题可以同时使用代入法和方程法。为快速解题可首先考虑方程法，设规定时间为x天，则（x-3）×l40=（x+3）×l20，解得x=39。故选D。

93、在同一环形跑道上小陈比小王跑得慢，两人都按同一方向跑步锻炼时，每隔12分钟相遇一次;若两人速度不变，其中一人按相反方向跑步，则隔4分钟相遇一次。问两人跑完一圈花费的时间小陈比小王多几分钟_____
A: 5B: 6C: 7D: 8
参考答案: B 本题解释:B【解析】不妨设小王和小陈速度分别为x，y，跑道长度为s，则两人都按同一方向跑步锻炼时，每隔12分钟相遇一次，说明s/（x-y）=12;若两人速度不变，其中一人按相反方向跑步，则每隔4分钟相遇一次，说明s/（x+y）=4;解得s=6x=12y，所以两人跑完一圈花费的时间小陈比小王多s/y-s/x=12-6=6分钟。

94、王家村西瓜大丰收后，全村男女老少分四个组品尝西瓜，且每组人正好一样，小伙子一个人吃1个，姑娘两个人吃1个，老人三个人吃1个，小孩四个人吃1个，一共吃了200个西瓜，问王家村品尝西瓜的共有_____
A: 368人B: 384人C: 392人D: 412人
参考答案: B 本题解释: 【解析】B。

95、黑母鸡下一个蛋歇2天，白母鸡下一个蛋歇1天，两只鸡共下10个蛋最多需要多少天？_____
A: 10 B: 11 C: 12 D: 13
参考答案: B 本题解释:【解析】B。黑鸡每3天下一个蛋，白鸡每2天下一个蛋。10天时间黑鸡10÷3＝3……1最多下4个蛋。白鸡最多下10÷2＝5个蛋；11天时间黑鸡11÷3＝3……2最多下4个蛋，白鸡11÷2＝5……1最多下6个蛋。因此一共下10个蛋至少需要11天。

96、一根木杆，第一次截去了全长的1/2，第二次截去所剩木杆的1/3，第三次截去所剩木杆的1/4，第四次截去所剩木杆的1/5，这时量得所剩木杆长为6厘米。问：木杆原来的长是多少厘米?_____
A: 15B: 26C: 30D: 60
参考答案: C 本题解释:【解析】：6÷（1-1/5）÷（1-1/4）÷（1-1/3）÷（1-1/2）=6÷（4/5×3/4×2/3×1/2）=6÷1/5=30（厘米）故本题选C。

97、有一笔奖金，按1：2：3的比例来分，已知第三人分450元，那么这笔奖金总共是_____元。
A: 1150 B: 1000 C: 900 D: 750
参考答案: C 本题解释:C。根据题意可知，这笔奖金共分为6份，而分到3份的第三人拿到了450元，则6份当是450×2=900元。所以正确答案为C项。

98、一列快车和一列慢车相对而行，其中快车车长200米，慢车车长250米，坐在慢车上的旅客看到快车驶过其所在窗口的时间是6秒钟，坐在快车上的旅客看到慢车驶过其所在窗口的时间是_____。
A: 6秒B: 6.5秒C: 7秒D: 7.5秒
参考答案: D 本题解释:D【解析】两车相向而行，故慢车、快车相对速度均为V（快）+V（慢），慢车走的路程为快车车长200米;同理，坐在快车上看慢车，走的距离为250米。故。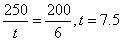

99、有一个矩形花园,长比宽多30米,现在花园的四周铺等宽的环路。已知路的面积是800M2,路的外周长是180m,问路宽是多少米?_____
A: 4B: 5C: 6D: 3
参考答案: B 本题解释:【答案】B。解析:设小矩形的宽是x,则长是x+30;设路宽是y,则大矩形的宽是x+2,大矩形的长是x+30+2y,已知条件可表示为(x+2y)(x+30+27)-x(x+30)=800和2(x+2y+x+30+2y)=180,解得y=5米。

100、有两个山村之间的公路都是上坡和下坡，没有平坦路。客车上坡的速度保持20千米/小时，下坡的速度保持30千米/小时。现知客车在两个山村之间往返一次，需要行驶4小时。请问这两个山村之间的距离有多少千米?_____
A: 45B: 48C: 50D: 24
参考答案: B 本题解释: 【解析】B。根据平均速度公式可知，全程的平均速度是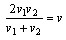：，全程的平均速度是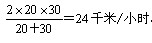：。（已知往返速度，求全程的平均速度，是有简便的算法的，要熟练把握。）两山村之间的路程是：（24×4）2=48千米。