1、某团体从甲地到乙地,甲、乙两地相距100千米,团体中一部人乘车先行,余下的人步行,先坐车的到途中某处下车步行,汽车返回接先步行的那部分人,已知步行速度为8千米/小时,汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间。_____
A: 5.5小时B: 5小时C: 4.5小时D: 4小时
参考答案: B 本题解释:正确答案是B考点行程问题解析
2、一本书有225页,某人第1天看了全书的1/9,第2天看了剩下的1/2,第3天就该从第_____页开始看。
A: 100B: 101C: 125D: 126
参考答案: D 本题解释:【答案】D。解析:第一天看了225×1/9=25页,第二天看了(225-25)×1/2=100页,第三天应从第25+100+1=126页开始看。故正确答案为D。
3、将棱长为1的正方体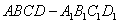 ,切去一角
,切去一角 后,剩下几何体的表面积是_____。
后,剩下几何体的表面积是_____。
A: 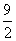 B: 5C:
B: 5C: 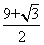 D:
D: 
参考答案: C 本题解释:参考答案:C题目详解:如右图所示,可知:原正方体表面积: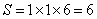 ;减少的表面积为:
;减少的表面积为: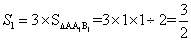 ;增加的表面积为:
;增加的表面积为: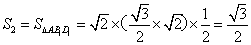 ;故剩下面积为:
;故剩下面积为: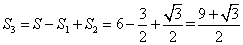 。所以,选C。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选C。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
4、一次知识竞赛,共3道题,每个题满分6分。给分时只能给出自然数0—6分。如果参加竞赛的人三道题的得分的乘积都是36分,并且任意两人三道题的得分不完全相同,那么最多有多少人参加竞赛? _____
A: 24B: 20C: 18D: 12
参考答案: D 本题解释:【解析】D。解析:36=1×6×6=2×3×6=3×3×4,三道题得1,6,6分有3种可能,三道题得2,3,6分有6中可能,三道题得3,3,4分有3种可能。故最多有3+6+3=12人。
5、甲、乙两地相距210公里,a、b两辆汽车分别从甲、乙两地同时相向出发并连续往返于两地,从甲地出发的a汽车的速度为90公里/小时,从乙地出发的b汽车的速度为120公里/小时。问a汽车第二次从甲地出发后与b汽车相遇时,b汽车共行驶了多少公里?_____
A: 560公里B: 600公里C: 620公里D: 630公里
参考答案: B 本题解释:正确答案是B考点行程问题解析a车第二次从甲出发前,经过一个往返的路程,即420公里,所用时间为420÷90=14/3小时;与此同时,b车经过路程为120×14/3=560公里,即一个往返路程加上140公里,此时ab两车位置如图所示。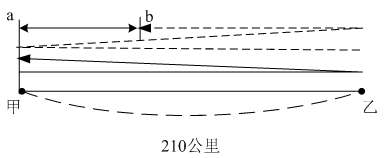 此时ab相距210-140=70公里,可知二者相遇于70÷(90+120)=1/3小时之后。整个过程中b共走过560+120×1/3=600公里。故正确答案为B。
此时ab相距210-140=70公里,可知二者相遇于70÷(90+120)=1/3小时之后。整个过程中b共走过560+120×1/3=600公里。故正确答案为B。
6、小明给住在五个国家的五位朋友分别写一封信,这些信都装错了信封的情况共有多少种?_____
A: 32B: 44C: 64D: 120
参考答案: B 本题解释:参考答案:B题目详解:套用“装错信封”问题的公式: ;即D5=44;所以,选B;考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
;即D5=44;所以,选B;考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
7、现有甲、乙两个水平相当的技术工人需进行三次技术比赛,规定三局两胜者为胜方。如果在第一次比赛中甲获胜,这时乙最终取胜的可能性有多大?_____。
A: 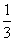 B:
B: 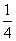 C:
C: 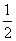 D:
D: 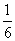
参考答案: B 本题解释:参考答案:B题目详解:令乙最终取胜的事件为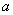 ,第一次比赛中甲获胜为事件
,第一次比赛中甲获胜为事件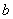 :则
:则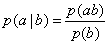 ;
;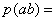 第一次比赛中甲获胜的概率×第二次乙获胜的概率×第三次乙获胜的概率
第一次比赛中甲获胜的概率×第二次乙获胜的概率×第三次乙获胜的概率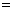
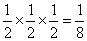 ;
;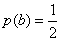 ;因此
;因此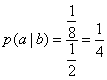 ;所以,选B。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选B。考查点:数量关系>数学运算>概率问题>条件概率
8、一共有20道题目,答对一道得5分,答错或不答扣一分,要答对多少道题,才能得82分?_____
A: 15B: 16C: 17D: 18
参考答案: C 本题解释:参考答案:C题目详解:根据题意,假设20道题目全部答对,可得:5×20=100分,答错一题或不答损失:5+1=6分,现在一共损失了:100-82=18分;则答错了:18÷6=3道题,答对了20-3=17道题。所以,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
9、新年晚会上,老师让每位同学从一个装有许多玻璃球的口袋中取两个球,这些球的手感相同,只有红、黄、白、蓝、绿五色之分,结果发现总有两个人取的球相同,由此可知,参加取球的至少有多少人?_____
A: 15B: 16C: 17D: 18
参考答案: B 本题解释:参考答案:B题目详解:解法一:摸两个球,则:两球的颜色不同的情况有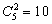 种,两个球颜色相同的情况有5种,摸两个球共有:10+5=15种情况,故最少有16人参加取球才能保证总有两个人取的球相同。解法二:五种颜色的球,2个一组,同色2个一组的情况有5种,不同色2个一组有
种,两个球颜色相同的情况有5种,摸两个球共有:10+5=15种情况,故最少有16人参加取球才能保证总有两个人取的球相同。解法二:五种颜色的球,2个一组,同色2个一组的情况有5种,不同色2个一组有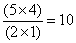 种情况,所以共有15种组合方式。总有两人取的球相同,参加取球人至少有16人考查点:数量关系>数学运算>抽屉原理问题>抽屉原理2
种情况,所以共有15种组合方式。总有两人取的球相同,参加取球人至少有16人考查点:数量关系>数学运算>抽屉原理问题>抽屉原理2
10、三个圆的半径都是5厘米,三个圆两两相交于圆心。求阴影部分的面积之和。_____ 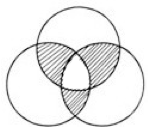
A: 29.25平方厘米B: 33.25平方厘米C: 39.25平方厘米D: 35.35平方厘米
参考答案: C 本题解释:正确答案是C考点几何问题解析使用割补法可知阴影部分的面积相当于半个圆的面积,则可得25π÷2=25×3.14÷2=39.25。故正确答案为C。
11、甲、乙两地相距100千米,张先骑摩托车从甲出发,1小时后李驾驶汽车从甲出发,两人同时到达乙地。摩托车开始速度是50千米/小时,中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟,那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 1(1/2)C: 1/3D: 2
参考答案: C 本题解释: C 解析: 汽车行驶100千米需100÷80=1(1/4)(小时),所以摩托车行驶了1(1/4)+1+1/6=2(5/12)(小时)。如果摩托车一直以40千米/小时的速度行驶,2(5/12)小时可行驶9623千米,与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷(50-40)=1/3(小时)。故本题选C。
12、在1至1000的1000个自然数中,既不是4的倍数,也不是6的倍数的数共有多少个?_____
A: 375B: 416C: 625D: 791
参考答案: C 本题解释:C【解析】1000÷4=250(个),所以1至1000中4的倍数的数有250个。1000÷6=166……4,所以1至1000中6的倍数的数有166个。1000÷(4×6)=41……16,说明1至1000中既是4的倍数,又是6的倍数的数有41个。即4的倍数的个数与6的倍数的个数的交集有41个,如图所示。所以1至1000中,既是4的倍数,也是6的倍数的数共有209+125+41=375(个)。则1至1000中,既不是4的倍数,也不是6的倍数的数共有:1000-(209+125+41)=1000-375=625(个)。故本题选C。
13、有一盒乒乓球,每次8个8个的数,10个10个的数,12个12个的数,最后总是剩下3个。但是9个9个数,刚好数完,问这盒乒乓球至少有多少个?_____
A: 144B: 180C: 243D: 324
参考答案: C 本题解释:参考答案:C题目详解:每次8个8个的数,10个10个的数,12个12个的数,最后总是剩下3个,因此此题是余数问题中余同的情况。即根据"余同取余,最小公倍数做周期"可知:8、10、12的最小公倍数120,只需要用3加上最小公倍数,直至能够被9整除为止;容易得到, ,正好能够被9整除,因此,这盒乒乓球至少有243个。所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>余同
,正好能够被9整除,因此,这盒乒乓球至少有243个。所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>余同
14、如果l※4=1234,2※3=234,7※2=78,那么4※5=_____。
A: 456B: 45678C: 5678D: 56789
参考答案: B 本题解释:参考答案:B题目详解:根据题意,可得:1※4表示从1开始的4个连续自然数,即为1234;同理2※3表示从2开始的3个连续自然数,即为234;7※2表示从7开始的2个连续自然数,即为78;所以4※5表示的是从4开始的5个连续自然数,即为45678。所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
15、某商店以每件6元的进价买回一批商品,售价为每件8.4元,当卖了这批商品的3/4时,不仅收回了购买这批商品所付的款项,而且还获得利润90元,这批商品有多少件?_____
A: 500 B: 600 C: 300 D: 400
参考答案: C 本题解释:【解析】C。 设这批商品有x件,可列方程:x×6=34x×8.4-90,解得x=300,所以本题答案为C。
16、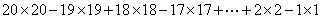 的值是_____。
的值是_____。
A: 210B: 240C: 273D: 284
参考答案: A 本题解释:参考答案:A题目详解:原式=(20×20-19×19)+(18×18-17×17)+…+(2×2-1×1)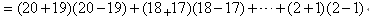
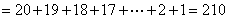 考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
17、甲、乙两种含金样品熔成合金,如甲的重量是乙的一半,得到含金  的合金;如甲的重量是乙的3.5倍,得到含金
的合金;如甲的重量是乙的3.5倍,得到含金  的合金。那么乙的含金量为_____。
的合金。那么乙的含金量为_____。
A:  B:
B:  C:
C:  D:
D: 
参考答案: A 本题解释:参考答案:A题目详解:解法一:设甲的含金量为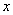 ,乙的含金量为
,乙的含金量为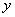 ,可列方程:
,可列方程: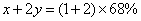
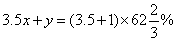 解得
解得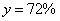 。所以,选A。解法二:设甲重量单位1,含量a,乙含量是b
。所以,选A。解法二:设甲重量单位1,含量a,乙含量是b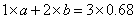
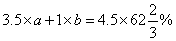 解得,
解得,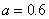 ,
, 所以,选A。考查点:数量关系>数学运算>和差倍比问题>比例问题
所以,选A。考查点:数量关系>数学运算>和差倍比问题>比例问题
18、甲、乙、丙三队在A、B两块地植树,A地要植树900棵,B地要植树1250棵,已知甲、乙、丙每天分别能植树24,30,32棵,甲在A地植树,丙在B地植树,乙先在A地植树,然后转到B地植树。两块地同时开始同时结束,乙应在开始后第几天从A地转到B地?_____
A: 5B: 7C: 9D: 11
参考答案: D 本题解释:D【解析】 植树共需(900+1250)÷(24+30+32)=25(天)。乙应在A地干(900-24×25)÷30=10(天),第11天转到B地。故本题正确答案为D。
19、某部队战士排成了一个6行、8列的长方阵。现在要求各行从左至右1,2,1,2,1,2,1,2报数,再各列从前到后1,2,3,1,2,3报数。问在两次报数中,所报数字不同的战士有_____。
A: 18个B: 24个C: 32个D: 36个
参考答案: C 本题解释:正确答案是C考点计数模型问题解析 标签画图分析
标签画图分析
20、建造一个容积为16立方米,深为4米的立方体无盖水池,如果池底和池壁的造价分别为每平方米160元和每平方米100元,那么该水池的最低造价是多少元?_____
A: 3980B: 3560C: 3270D: 3840
参考答案: D 本题解释:正确答案是D考点函数最值问题解析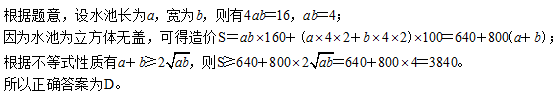 标签公式应用
标签公式应用
21、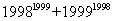 的尾数是_____:
的尾数是_____:
A: 3B: 6C: 7D: 9
参考答案: A 本题解释:参考答案:A题目详解:备注:用户“lumin”(2010-10-0222:00:56),认为:题有问题!正确答案应该是“尾数7”但经过分析,我们认为该题没有问题,答案也不存在歧义考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的重新排列
22、一个两位数的中间再加上一个0,那么所得的这个数是原数的9倍,原来这个两位数是多少?_____
A: 15B: 25C: 35D: 45
参考答案: D 本题解释:正确答案是D考点计算问题解析解析1:设这个两位数个位是x,十位是y,则100y+x=9(10y+x),4x=5y,符合要求的个位数x只有5,所以y=4,所以结果为45。解析2:四个选项直接代入,只有D符合要求。所以正确答案为D。秒杀技根据整除特性,一个数如果是9的倍数,那么这个数各位相加也是9的倍数。而插入的是0,所以原两位数各位相加也是9的倍数,只有D符合。标签直接代入数字特性
23、某企业有员工500人,其中60%的员工是男性,则该企业男员工比女员工多_____人。
A: 100B: 200C: 300D: 400
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析由题意可得,男性比女性多500×60%-500×40%=100人。故正确答案为A。
24、每条长200米的三个圆形跑道共同相交于A点,张三、李四、王五三个队员从三个跑道的交点A处同时出发,各取一条跑道练习长跑。张三每小时跑5公里,李四每小时跑7公里,王五每小时跑9公里。问三人第四次在A处相遇时,他们跑了多长时间?_____
A: 40分钟B: 48分钟C: 56分钟D: 64分钟
参考答案: B 本题解释:参考答案B题目详解:他们第四次相遇时:三人跑的路程一定均为200的整数倍;而三个人的速度分别为250/3米/分,350/3米/分,450/3米/分;因此三人第四次相遇时:跑的时间一定是3的整数倍;只有B项符合;所以,选B。考查点:数量关系>数学运算>行程问题>追及问题>环线追及问题>环线多次追及问题
25、有甲、乙两只钟表,甲表8时15分时,乙表8时31分。甲表比标准时间每9小时快3分,乙表比标准时间每7小时慢5分。至少要经过几小时,两钟表的指针指在同一时刻?_____
A: 12(7/11)B: 15C: 15(3/11)D: 17(8/11)
参考答案: C 本题解释: C 解析: 甲表比标准时间每小时快3/9=1/3分,乙表比标准时间每小时慢5/7分。甲、乙两表每小时相差是1/3+5/7=22/21分8时31分-8时15分=16分按追及问题,追及路程为16分,速度差是每小时22/21分,求追及时间。16÷22/21=16×21/22=15(3/11)(小时)至少再经过15311小时,两钟表的指针指在同一时刻。
26、银行一年定期存款利率是4. 7%,两年期利率是5. 1%,且利率税扣除20%,某人将1000元存三年,三年后本息共多少元?_____
A: 1074.5B: 1153.79C: 1149.0D: 1122.27
参考答案: D 本题解释:D 解析: 1000×(1+4. 7%×80%)×(1+5. 1%×2×80%)=1122. 27(元)。故本题选D。
27、_____ 
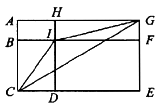
A: AB: BC: CD: D
参考答案: D 本题解释:正确答案是D考点几何问题解析 故正确答案为D。
故正确答案为D。
28、(2007北京应届,第24题)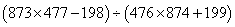 的值是_____。
的值是_____。
A: 1B: 2C: 3D: 4
参考答案: A 本题解释:参考答案:A题目详解:解法一:鉴于题中数字两两相近,可以采用整体消去法:原式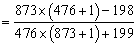
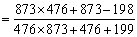
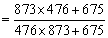 =1;所以,选A。解法二:
=1;所以,选A。解法二:
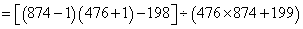
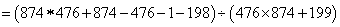
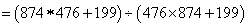 =1;所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>消去法
=1;所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>消去法
29、某班46个同学要在A、B、C、D、E五位候选人中选出一位体育委员。已知A得选票25张,B得选票占第二位,C、D得票相同,而E选票最少,只得4票。那么B得了多少张选票?_____
A: 7张B: 9张C: 6张D: 4张
参考答案: A 本题解释:【解析】由题干可知,B、C、D三人共得选票46-25-4=17(张)。设C、D每人得票数为m,B得票数为n,则有2m+n=17(n>m),则m=5,n=7。故B得选票为7张。
30、已知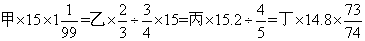 ,则甲、乙、丙、丁四个数中最大的是哪个?_____
,则甲、乙、丙、丁四个数中最大的是哪个?_____
A: 甲B: 乙C: 丙D: 丁
参考答案: B 本题解释:参考答案:B题目详解:原式化简为=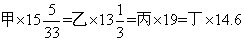 ,乘以的数字越小,说明放大的倍数越小,则原数字越大。所以,选B考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
,乘以的数字越小,说明放大的倍数越小,则原数字越大。所以,选B考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
31、8点28分,时钟的分针与时针的夹角(小于180)是多少度?_____
A: 86B: 87C: 88D: 89
参考答案: A 本题解释:参考答案:A题目详解:8点整时:时针的度数为240°;经过28分钟:该夹角为240-(6-0.5)×28=86度;所以,选A。考查点:数量关系>数学运算>特殊情境问题>钟表问题>时针与分针的角度关系
32、下列数中最大的是_____。
A: 599×601B: 598×602C: 590×610D: 500×700
参考答案: A 本题解释:正确答案是A考点计算问题解析对比可见,四组乘数中,其前一个乘数依次减小,后一个乘数依次增大。只要对比A,D两项的数字孰大孰小就可以知道答案了。599×601≈36000,500×700=35000。A项的数明显大于D项,由此可知A项的数最大。故正确答案为A。
33、有一1500米的环形跑道,甲、乙两人同时同地出发,若同方向跑50分钟后,甲比乙多绕整一圈;若以相反方向跑2分钟后二人相遇,则乙的速度为_____。
A: 330米/分钟B: 360米/分钟C: 375米/分钟D: 390米/分钟
参考答案: B 本题解释:参考答案:B题目详解:同方向跑时,可以计算出甲、乙速度差为: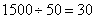 (米/分钟);反方向跑时,可以计算出甲、乙两人速度和为:
(米/分钟);反方向跑时,可以计算出甲、乙两人速度和为: (米/分);乙的速度为:
(米/分);乙的速度为: (米/分),故选B。考查点:数量关系>数学运算>行程问题>相遇问题>环线相遇问题>环线多次相遇问题
(米/分),故选B。考查点:数量关系>数学运算>行程问题>相遇问题>环线相遇问题>环线多次相遇问题
34、(2008安徽,第15题)某企业有甲、乙、丙三个仓库,且都在一条直线上,之间分别相距l千米、3千米,三个仓库里面分别存放货物5吨、4吨、2吨。如果把所有的货物集中到一个仓库,每吨货物每千米运费是90元,请问把货物放在哪个仓库最省钱?_____
A: 甲B: 乙C: 丙D: 甲或乙
参考答案: B 本题解释:参考答案:B题目详解:此题遵循“小往大处靠”原则,先把2吨的货物移动到4吨那,这样就相当于有了6吨货物,然后在把5吨的货物也移动到6吨,综上所述,运到乙仓库最省钱考查点:数量关系>数学运算>统筹问题>货物集中问题
35、一段路程分为上坡、平路、下坡,三段路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米,路程全长是50千米,小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A 本题解释:A解析:上坡、平路、下坡的速度之比是:14∶25∶36=5∶8∶10平路速度为:3×8/5=24/5(千米/小时)下坡速度为:3×10/5=6(千米/小时)上坡路程为:50×1/(1+2+3)=50/6=25/3(千米)平路路程为:50×2/(1+2+3)=50/3(千米)下坡路程为:50×3/(1+2+3)=25(千米)小龙走完全程用的时间为:25/3÷3+50/3÷24/5+25÷6=10(5/12)(小时)故本题选A。
36、有37名红军战士渡河,现仅有一只小船,每次只能载5人,需要几次才能渡完?_____
A: 7次B: 8次C: 9次D: 10次
参考答案: C 本题解释:正确答案是C考点计数模型问题解析 标签公式应用
标签公式应用
37、某广场有一块面积为160平方米的路面,用白色、紫色、黑色三种大理石铺成,每块大理石的面积是0.4平方米,其中白色大理石150块,紫色大理石50块,其余的是黑色大理石,某人在上面行走,他停留在黑色大理石上的概率是多少?_____。
A: 1/4B: 2/5C: 1/3D: 1/6
参考答案: A 本题解释:正确答案是A考点概率问题解析一共有大理石160÷0.4=400块,因此有黑色大理石400-150-50=200块。计算概率是需考虑两只脚分跨两块大理石的情况,所以一只脚踩在黑色大理石上的概率为200÷400=0.5,另一只也是0.5,则此人停留在黑色大理石上的概率为:0.5×0.5=0.25,故正确答案为A。
38、已知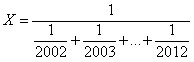 ,问X的整数部分是多少?_____
,问X的整数部分是多少?_____
A: 182B: 186C: 194D: 196
参考答案: A 本题解释:A【解析】由题意可知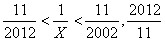 的整数部分是182,
的整数部分是182,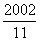 的整数部分也是182,因此X的整数部分也是182。
的整数部分也是182,因此X的整数部分也是182。
39、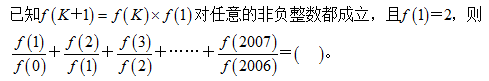 _____
_____
A: 4012B: 4013C: 4014D: 4016
参考答案: C 本题解释:正确答案是C解析由题中条件可知,原式=f(1)×2007=2×2007=4014,故正确答案为C。考点计算问题
40、某村村民经过集体投票民主选举村干部,5位村干部候选人中得票最高者将当选。经统计,本次选举有效选票一共395票,且当选者的得票数比其他4位候选人的平均得票数要多60票,则这名当选者一共获得_____票。
A: 62B: 67C: 122D: 127
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析假定其他四位候选人的平均票数为M,则根据题意可得4M+M+60=395,解得M=67,因此当选者一共获得67+60=127票。故正确答案为D。
41、赵先生34岁,钱女士30岁,一天,他们碰上了赵先生的三个邻居,钱女士问起了他们的年龄,赵先生说:他们三人的年龄各不相同,三人的年龄之积是2450,三人的年龄之和是我俩年龄之和。问三个邻居中年龄最大的是多少岁?_____
A: 42B: 45C: 49D: 50
参考答案: C 本题解释:正确答案是C考点年龄问题解析三个人的年龄之积为2450,对2450做因式分解得2450=2×5×5×7×7,三个人的年龄之和为64。所以试着把5个因数组合成3个不同的整数,使他们的和为64。可知5、10、49符合要求,5+10+49=64,故三个邻居中年龄最大是49岁。故正确答案为C。标签构造调整
42、有一项工作任务,小明先做4小时,小方接着做8小时可以完成,小明先做6小时,小方接着做4小时也可以完成,如果小明先做2小时后再让小方接着做,那么小方可以完成工作还需要几个小时?_____
A: 8B: 10C: 11D: 12
参考答案: D 本题解释:正确答案是D考点工程问题解析解析1:小明先做4个小时,小方接着做8个小时可以完成,小明先做6个小时,小方接着做4个小时完成,即小明先增加2个小时工作,小方后面可以减小4个小时的工作(反之亦然),如果小明先只工作2个小时,即比第一种情况小明减少了2个小时工作,小方必须增加4个小时的工作,所以小明接着工作8+4=12(小时),故正确答案为D。解析2:设总的任务为为1,则小明的效率为x,小方的效率为y,则有4x+8y=1,6x+4y=1,解得x=1/8,y=1/16,则小明做2小时还剩1-2×(1/8)=3/4,小方还需要做3/4÷1/16=12(小时),故正确答案为D。
43、某旅游景点商场销售可乐,每买3瓶可凭空瓶获赠1瓶可口可乐,某旅游团购买19瓶,结果每人都喝到了一瓶可乐,该旅游团有多少人?_____
A: 19B: 24C: 27D: 28
参考答案: D 本题解释: D 解析:由题意知:买2瓶可乐就可以喝3瓶,所以19:N=2:3,N=28.5,商家不可能亏本,所以取28,选D。
44、现有篮球、排球、乒乓球、足球、网球五门选修课,每名学生必须要从中选出而且仅选择2门选修课,问至少有多少名学生进行选课,才能保证至少有6名学生所选的选修课相同?_____
A: 48B: 50C: 51D: 70
参考答案: C 本题解释:【答案】C。解析:要求五门课程选出两门,共有C25=10种,要至少有6名学生所选的选修课相同,那么这10中选课方式各有5名学生选择,共有10×5=50人,之后再来一人,就可以保证有6名学生所选的选修课相同,则为50+1=51人,所以答案为C。
45、(2006国家,第41题)某市居民生活用电每月标准用电量的基本价格为每度0.50元,若每月用电量超过标准用电量,超出部分按其基本价格的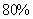 收费,某户九月份用电84度,共交电费39.6元,则该市每月标准用电量为多少度?_____
收费,某户九月份用电84度,共交电费39.6元,则该市每月标准用电量为多少度?_____
A: 60度B: 65度C: 70度D: 75度
参考答案: A 本题解释:参考答案:A题目详解:解法一:采用十字交叉法: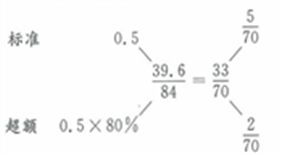
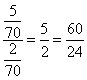 由于总用电为84度,所以标准、超额分别为60、24度。解法二:设每个月标准用电为x,则根据题意,可列方程:
由于总用电为84度,所以标准、超额分别为60、24度。解法二:设每个月标准用电为x,则根据题意,可列方程: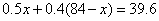
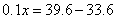
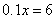
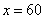 所以,该市每月标准用电量为60度。因此,选A。考查点:数量关系>数学运算>特殊情境问题>分段计算问题
所以,该市每月标准用电量为60度。因此,选A。考查点:数量关系>数学运算>特殊情境问题>分段计算问题
46、某班男生比女生人数多80%,一次考试后,全班平均成级为75分,而女生的平均分比男生的平均分高20%,则此班女生的平均分是_____。
A: 84B: 85C: 86D: 87
参考答案: A 本题解释:正确答案是A设男生的平均分为y,则女生的平均分是1.2y,根据整除特性可知,女生的平均分数肯定能够被12整除,观察四个选项,只有A选项84能够被12整除,故A为正确选项。
47、某工厂生产的零件总数是一个三位数,平均每个车间生产了35个,统计员在记录时粗心地将该三位数的百位数与十位数对调了,结果统计的零件总数比实际总数少270个,问该工厂所生产的零件总数最多可能是多少个?_____
A: 525B: 630C: 855D: 960
参考答案: B 本题解释:正确答案是B考点多位数问题解析由平均每个车间生产了35个可知,零件总数能够被35整除,仅A、B符合;观察这两个选项,百位数与十位数对调后差值均为270,要求最大值,显然630更大,故正确答案为B。
48、有20名工人修筑一段公路,计划15天完成。动工3天后抽出5人去其他工地,其余人继续修路。如果每人工作效率相同且不变,那么修完这段公路实际用_____。
A: 19天B: 18天C: 17天D: 16天
参考答案: A 本题解释:正确答案是A考点工程问题解析解析1:设总工程为300,则每人每天工作量为300÷15÷20=1。第一阶段3天20人共完成工作量为3×20=60,第二阶段工作量为300-60=240,剩余15人每天完成工作量为15,还需240÷15=16天,则总共需3+16=19天。解析2:去其他工地的5人12天共完成工作量为5×12=60,需要剩余的15人工作60÷15=4天,则修完这条公路总共需要15+4=19天。故正确答案为A。标签赋值思想
49、某学校入学考试,确定了录取分数线。在报考的学生中,只有1/3被录取,录取者平均分比录取分数线高6分,没有被录取的学生其平均分比录取分数线低15分,所有考生的平均分是80分,推知录取分数线是_____。
A: 80B: 84C: 88D: 90
参考答案: C 本题解释:【答案】C。解析:不难看出,总共有多少人参加考试对本题的最终结果没有影响,仅是录取分数线的1/3对结果有影响,也即最后结果只与这个比例有关,而与总数无关。那么就可以直接看做录取了1个人,有2个人没录取,总人数为3人,则假定录取分数线为x分,于是得方程:(x﹢6)﹢(x-15)×2=80×3,解得x=88。故正确答案为C。
50、超市规定每3个空汽水瓶可以换一瓶汽水,小李有11个空汽水瓶,最多可以换几瓶汽水_____。
A: 5B: 4C: 3D: 2
参考答案: A 本题解释:正确答案是A考点计数模型问题解析3个空瓶换1瓶水,因此3空瓶=1汽水+1空瓶,可以得出等价公式:2空瓶=1汽水,因此小李的11个空汽水瓶可以换5瓶汽水。故正确答案为A。
51、在1000以内,除以3余2,除以7余3,除以11余4的数有多少个?_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:正确答案是B考点余数与同余问题解析同余问题,不符合“余同取余,和同加和,差同减差,最小公倍数做周期”的口诀,通过余数组获得通式。除以3余2的余数组为2、5、8、11、14、17、···;除以7余3的余数组为3、10、17、···。结合此两者可知满足前两条的被除数可写成21n+17,其余数组为17、38、59、···;而除以11余4的余数组为4、15、26、37、48、59、···。结合此两者可知满足三条的被除数可写成231n+59。由题意:0≤231n+59≤1000,解得0≤n≤4。所以这样的数共有5个,故正确答案为B。口诀解释:余同取余,例如“一个数除以7余1,除以6余1,除以5余1”,可见所得余数恒为1,则取1,被除数的表达式为210n+1;和同加和,例如“一个数除以7余1,除以6余2,除以5余3”,可见除数与余数的和相同,取此和8,被除数的表达式为210n+8;差同减差,例如“一个数除以7余3,除以6余2,除以5余1”,可见除数与余数的差相同,取此差4,被除数的表达式为210n-4。特别注意前面的210是5、6、7的最小公倍数。
52、2011×201+201100—201.1×2910的值为_____。
A: 20110B: 21010C: 21100D: 21110
参考答案: A 本题解释:原式=2011×(201+100—291)=2011×10=20110。故选A。
53、有一船从A城到B城,顺水时需要 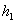 小时,逆水时需要
小时,逆水时需要  小时,如果两城之间距离是
小时,如果两城之间距离是 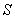 ,那么往返两城一次,平均速度为_____。
,那么往返两城一次,平均速度为_____。
A: 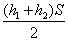 B:
B: 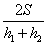 C:
C: 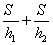 D:
D: 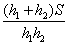
参考答案: B 本题解释:参考答案:.B题目详解:根据公式,可知:平均速度=总路程/总时间,总路程是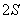 ,总时间是
,总时间是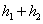 ,所以平均速度是
,所以平均速度是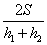 ;所以,选B。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
;所以,选B。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
54、三个单位共有180人,甲、乙两个单位人数之和比丙单位多20人,甲单位比乙单位少2人,求甲单位的人数_____。
A: 48人B: 49人C: 50人D: 51人
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析解析1:设甲单位的人数为x人,则乙单位的人数为(x+2)人,丙单位的人数为(x+x+2-20)即为(2x-18)人,根据题意可得:x+(x+2)+(2x-18)=180,解得x=49,故选择B选项。解析2:由“三个单位共有180人,甲、乙两个单位人数之和比丙单位多20人”可得甲、乙两单位人数之和为:(180+20)÷2=100,又知“甲单位比乙单位少2人”,因此甲单位人数为:(100-2)÷2=49,故选择B选项。故正确答案为B。
55、某运输队有大货车和小货车24辆,其中小货车自身的重量和载货量相等,大货车的载货量是小货车的1.5倍,自身重量是小货车的2倍。所有车辆满载时共重234吨,空载则重124吨,那么该运输队的大货车有多少辆? _____
A: 4B: 5C: 6D: 7
参考答案: D 本题解释:D【解析】设大货车数量为x,小货车自重量为a,小货车数量为24-x,列方程x?2a+(24-x)?a=124[x?2a+(24-x)?a]+x?1 5a+(24-x)?a=234 解得x=7。故选D。
56、李老师带领一班学生去种树,学生恰好被平分为4个小组,总共种树667棵,如果师生每人种树的棵数一样多,那么这个班共有学生多少人?_____
A: 28B: 36C: 22D: 24
参考答案: A 本题解释:参考答案:A题目详解: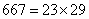 。这个班师生每人种树的棵数只能是667的约数:1、23、29、667。当每人种23棵树时,全班人数应是
。这个班师生每人种树的棵数只能是667的约数:1、23、29、667。当每人种23棵树时,全班人数应是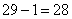 ,而28恰好是4的倍数,符合题目要求。以此方法计算,每人种1或29或667棵树时,所得人数不能被4整除,故不符合题目要求。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
,而28恰好是4的倍数,符合题目要求。以此方法计算,每人种1或29或667棵树时,所得人数不能被4整除,故不符合题目要求。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
57、把一根钢管锯成5段需要8分钟,如果把同样的钢管锯成20段需要多少分钟?_____
A: 32分钟B: 38分钟C: 40分钟D: 152分钟
参考答案: B 本题解释:正确答案是B考点计数模型问题解析锯成5段需要锯4次,即每次需要2分钟,而锯20段需要锯19次,因此需要:19×2=38分钟,故正确答案为B。
58、某鞋业公司的旅游鞋加工车间要完成一出口订单,如果每天加工50 双,要比原计划晚3 天完成,如果每天加工60 双,则要比原计划提前2 天完成,这一订单共需要加工多少双旅游鞋?_____
A: 1200 双 B: 1300 双 C: 1400 双 D: 1500 双
参考答案: D 本题解释:【答案】D[解析]能被50、60整除的,排除B和C,再依次代入A和D,A不符合,所以选D。
59、甲、乙两地相距100千米,张先骑摩托车从甲出发,1小时后李驾驶汽车从甲出发,两人同时到达乙地。摩托车开始速度是50千米/小时,中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟,那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 3/2C: 1/3D: 2
参考答案: C 本题解释: C解析:汽车行驶100千米需100÷80=5/4(小时),所以摩托车行驶了5/4+1+1/6=29/12(小时)。如果摩托车一直以40千米/小时的速度行驶,29/12小时可行驶96(2/3)千米,与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷(50-40)=1/3(小时)。故本题选C.
60、9e2006的个位数是_____。(9e2006表示9的2006次方)
A: 1B: 2C: 8D: 9
参考答案: A 本题解释:正确答案是A考点计算问题解析9的奇数次方尾数为9,偶数次方尾数为1,故9e2006的为数尾数为1,正确答案为A。
61、两港相距560千米,甲船往返两港需105小时,逆流航行比顺流航行多用了35小时。乙船的静水速度是甲船的静水速度的2倍,那么乙船往返两港需要多少小时?_____
A: 24B: 20C: 28D: 48
参考答案: D 本题解释:参考答案:.D题目详解:甲船往返航行的时间分别是: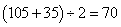 小时,70/2=35甲船逆水速度:
小时,70/2=35甲船逆水速度: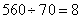 千米/小时,甲船顺水速度:
千米/小时,甲船顺水速度: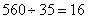 千米/小时,甲船在静水中的速度是:
千米/小时,甲船在静水中的速度是: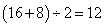 千米/小时,水流的速度是:
千米/小时,水流的速度是: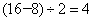 千米/小时;乙船在静水中的速度是:
千米/小时;乙船在静水中的速度是: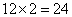 千米/小时,乙船往返一次所需要的时间是:
千米/小时,乙船往返一次所需要的时间是: 小时。所以,选D。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
小时。所以,选D。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
62、河道赛道场长120米,水流速度为2米/秒,甲船速度为6米/秒,乙船速度为4米/秒。比赛进行两次往返,甲、乙同时从起点出发,先顺水航行,问多少秒后甲 、乙船第二次迎面相遇?_____
A: 48B: 50C: 52D: 54
参考答案: C 本题解释:【答案】C。解析:甲船顺水速度为2+6=8米/秒,逆水速度为6-2=4米/秒;乙船顺水速度为2+4=6米/秒,逆水速度为4-2=2米/秒。
63、(2005北京社招,第13题)某剧院有25排座位,后一排比前一排多2个座位,最后一排有70个座位。这个剧院共有多少个座位?_____
A: 1104B: 1150C: 1170D: 1280
参考答案: B 本题解释:参考答案:B题目详解:解法一:根据项数公式: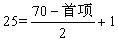 得首项=22。根据求和公式:
得首项=22。根据求和公式: 选择B。[注释]因为剧院一共有25排座位,所以座位总数肯定是25的倍数,马上得出答案为B。解法二:第一排有
选择B。[注释]因为剧院一共有25排座位,所以座位总数肯定是25的倍数,马上得出答案为B。解法二:第一排有 个座位所以总座位数是
个座位所以总座位数是 个考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
个考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
64、小赵,小钱,小孙一起打羽毛球,每局两人比赛,另一人休息,三人约定每一局的输方下一局休息,结束时算了一下,小赵休息了2局,小钱共打了8局,小孙共打了5局,则参加第9局比赛的是_____。
A: 小钱和小孙B: 小赵和小钱C: 小赵和小孙D: 以上皆有可能
参考答案: B 本题解释:正确答案是B考点统筹规划问题解析本题关键在于三个人打羽毛球,一个人休息的时候必然是另外两个人比赛的时候。因此条件“小赵休息了2局”,说明小钱和小孙对战了2局,则两人其余的比赛都是和小赵进行的,于是总的比赛局数为8+5-2=11局。三人比赛中,任何一个人不可能连续休息两场,也即每个人的休息场次只能是间隔的,而11局比赛中小孙打了5局,休息了6局,那么他只能是这11局中的第2、4、6、8、10局中上场。因此第9局比赛中小孙没有上场,也即参加比赛的是小赵和小钱。故正确答案为B。
65、某市举办经济建设成就展,计划在六月上旬组织5个单位参观,其中1个单位由于人数较多,需要连续参观2天,其他4个单位只需参观1天。若每天最多只能安排一个单位参观,则参观的时间安排共有_____种。
A: 630B: 700C: 15120D: 16800
参考答案: C 本题解释:正确答案是C考点排列组合问题解析 标签公式应用
标签公式应用
66、已知正整数数列{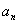 }满足
}满足 ,且第七项等于18,则该数列的第10项为_____。
,且第七项等于18,则该数列的第10项为_____。
A: 5道B: 6道C: 7道D: 8道
参考答案: C 本题解释:参考答案:C题目详解:设总题数位x,两人都没答对的题目为y: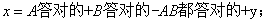
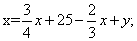 解得,
解得, 又因为,x是12的倍数,
又因为,x是12的倍数, 在这个区间上,唯一的12的倍数是36;所以,
在这个区间上,唯一的12的倍数是36;所以,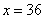 时,
时,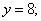 所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>不等式问题>由不等式确定未知量取值范围
所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>不等式问题>由不等式确定未知量取值范围
67、有面积为1平方米、4平方米、9平方米、16平方米的正方形地毯各10块,现有面积为25平方米的正方形房间需用以上地毯来铺设,要求地毯互不重叠且而好铺满。问最少需几块地毯? _____
A: 6块B: 8块C: 10块D: 12块
参考答案: B 本题解释:最少需地毯块数,即尽量用大面积的地毯,25=16+9×1 ——10块25=9+3×4+4×1——8块25=4×4+9×1 ——13块,所以最小块数为8.具体是一块9平方米,三块4平方米。四块1平方米,选B。
68、把黑桃、红桃、方片、梅花四种花色的扑克牌按黑桃10张、红桃9张、方片7张、梅花5张的顺序循环排列。问第2015张扑克牌是什么花色?_____
A: 黑桃B: 红桃C: 梅花D: 方片
参考答案: C 本题解释:正确答案是C考点周期问题解析由题意可知,每个大周期为10+9+7+5=31,2015÷31=65,没有余数,说明第2015张为大周期中的最后一张牌的花色,即梅花。故正确答案为C。
69、 _____
_____
A: AB: BC: CD: D
参考答案: B 本题解释:正确答案是B考点计算问题解析 故正确答案为B。
故正确答案为B。
70、_____ 
A: AB: BC: CD: D
参考答案: B 本题解释:正确答案是B考点几何问题解析因为正三角形的周长和正六边形的周长相等,又因为正三角形和正六边形的边长的个数比是1:2,所以其边长之比为2:1,假设正三角形的边长为2,则正六边形的边长为1。正六边形可以分成6个小正三角形,如下图所示,边长为1的小正三角形面积:加长为2的正三角形面积=1:4。所以正六边形面积:正三角形面积=6:4=1.5,故正确答案为B。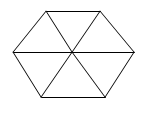 标签赋值思想
标签赋值思想
71、某家店准备打折出售一批滞销的电脑,经核算,如果按正价打九折销售,每台还可盈利305元,如果打八折,就要亏损175元。那么这种电脑的进货价是_____元。
A: 4800B: 4625C: 4015D: 3940
参考答案: C 本题解释:这种电脑打九折和打八折的差价是305+175=480(元),那么正价为480÷(90%-80%)=4800(元),进货价为4800×90%-305=4015(元)。故本题答案为C。
72、分数4/9、17/35、101/203、3/7、151/301中最大的一个是_____。
A: 4/9B: 17/35C: 101/203D: 151/301
参考答案: D 本题解释:D【解析】首先目测可以知道3/7、17/35和101/203都小于1/2,而4/9和151/301都大于1/2,所以只要比较二者的大小就可以,通过计算,151/301大,所以选择D。
73、有8个队参加比赛,采用所示的淘汰制方式。问在比赛前抽签时,可以得到多少种实质不同的比赛安排表?_____ 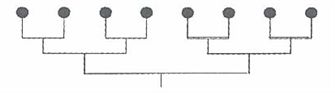
A: 4030B: 315C: 5040D: 164
参考答案: B 本题解释:参考答案:B题目详解:我们标上字母如图:全排列为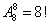 。因为A/B,B/A实质赛程一样;同理:C/D,E/F,G/H,I/J,K/L,M/N均是,所以除以7个2。于是,共有
。因为A/B,B/A实质赛程一样;同理:C/D,E/F,G/H,I/J,K/L,M/N均是,所以除以7个2。于是,共有 种实质不同的赛程安排。所以,选B。
种实质不同的赛程安排。所以,选B。 考查点:数量关系>数学运算>排列组合问题>比赛问题>淘汰赛
考查点:数量关系>数学运算>排列组合问题>比赛问题>淘汰赛
74、(2006北京社招,第18题)有-水池,池底有泉水不断涌出,要想把水池的水抽干,l0台抽水机需抽8小时,8台抽水机需抽12小时,如果用6台抽水机,那么需抽多少小时?_____
A: 16B: 20C: 24D: 28
参考答案: C 本题解释:参考答案:C题目详解:依题意:设泉水的原有存量为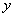 ;单位时间进水量即自然增长速度为
;单位时间进水量即自然增长速度为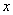 ;存量完全消失所消耗的时间
;存量完全消失所消耗的时间 为所求;代入公式:
为所求;代入公式: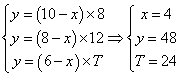 所以,选C。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
所以,选C。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
75、五个数写成一排,前三个数平均值是15,后两个数平均值是10,则这五个数的平均值是_____。
A: 11B: 12.5C: 13D: 14
参考答案: C 本题解释:正确答案是C考点平均数问题解析根据题干可知,前三个数的和为15×3=45,后两个数的和为10×2=20,则五个数的和为65,其平均数为13。故正确答案为C。
76、分多次用等量清水去冲洗一件衣服,每次均可冲洗掉上次所残留污垢的3/4,则至少需要多少次才可使得最终残留的污垢不超过初始污垢的1%?_____
A: 3B: 4C: 5D: 6
参考答案: B 本题解释:正确答案是B考点浓度问题解析由题意可得,(1-3/4)^n≤1%,4^n≥100,则n≥4,故正确答案为B。
77、同学们进行队列训练,如果每排8人,最后一排6人;如果每排10人,最后一排少4人。参加队列训练的学生最少有多少人?_____
A: 46B: 54C: 62D: 66
参考答案: A 本题解释:参考答案:A题目详解:每排10人,最后一排少4人,换种方式理解就是最后一排站了6人:因此此题是余数问题中余同的情况,"余同取余,最小公倍数做周期"可知:8和10的最小公倍数是40。因此,这些学生至少有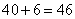 人。所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>余同
人。所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>余同
78、某单位今年一月份购买5包A4纸、6包B5纸,购买A4纸的钱比B5纸少5元;第一季度该单位共购买A4纸15包、B5纸12包,共花费510元。那么每包B5纸的价格比A4纸便宜_____。
A: 1.5元B: 2.0元C: 2.5元D: 3.0元
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析设A4纸和B5纸的价格分别为x元和y元。根据题意可得6y-5x=5,15x+12y=510,解得x=20,y=17.5,那么B5纸的价格比A4纸便宜20-17.5=2.5元。故正确答案为C。
79、一段路程分为上坡、平路、下坡三段,路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米,路程全长是50千米,小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A 本题解释: A解析:上坡、平路、下坡的速度之比是:14∶25∶36=5∶8∶10平路速度为:3×8/5=24/5(千米/小时)下坡速度为:3×10/5=6(千米/小时)上坡路程为:50×1/(1+2+3)=50/6=25/3(千米)平路路程为:50×2/(1+2+3)=50/3(千米)下坡路程为:50×3/(1+2+3)=25(千米)25/3÷3+50/3÷24/5+25÷6=10(5/12)(小时)故本题选A。
80、从某车站以加速度为1/18米/秒2始发的甲列车出发后9分钟,恰好有一列与甲列车同方向,并以50米/秒作匀速运行的乙车通过该车站,则乙车运行多少分钟与甲车距离为最近?_____
A: 9B: 3C: 5D: 6
参考答案: D 本题解释:D。当甲车速度小于乙车时,乙车逐渐缩短与甲车的距离;当甲车速度大于乙车时,两车之间距离拉大;仅当两车速度相同时,两车距离最小。根据Vt=Vo+at,可得50=1/18×9×60+1/18×t,求得t=360秒=6分钟。
81、某高校对一些学生进行问卷调查。在接受调查的学生中,准备参加注册会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备选择两种考试都参加的有46人,不参加其中任何一种考试的都15人。问接受调查的学生共有多少人?_____
A: 120B: 144C: 177D: 192
参考答案: A 本题解释:正确答案是A考点容斥原理问题解析假设只参加一种考试的有X人,则可知:X+46×2+24×3=63+89+47,可知X=35,因此接受调查的学生共有35+46+24+15=120人。故正确答案为A。注:将只符合一个条件、只符合两个条件和三个条件都符合的分别看作三个整体,以A、B、C表示三个集合,以X、Y、Z分别表示只符合一个条件、只符合两个条件和三个条件都满足的部分,则有A+B+C=X+2Y+3Z及A∪B∪C=X+Y+Z成立。
82、龟兔赛跑,全程5.2千米,兔子每小时跑20千米,乌龟每小时跑3千米,乌龟不停的跑;兔子边跑边玩,它先跑了1分钟后玩了15分钟,又跑了2分钟后玩15分钟,再跑3分钟后玩15分钟,以此类推。那么先到达终点比后到达终点的快多少分钟?_____
A: 10B: 20C: 15D: 13.4
参考答案: D 本题解释:参考答案D题目详解:乌龟刚时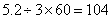 分钟;兔子总共跑了
分钟;兔子总共跑了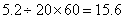 分钟。
分钟。 ,兔子一共休息了5次,共
,兔子一共休息了5次,共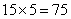 分钟。所以兔子共用时:
分钟。所以兔子共用时: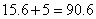 分钟。兔子先到达终点,比后到达终点的乌龟快
分钟。兔子先到达终点,比后到达终点的乌龟快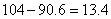 分钟。考查点:数量关系>数学运算>行程问题>追及问题>直线追及问题>直线一次追及问题
分钟。考查点:数量关系>数学运算>行程问题>追及问题>直线追及问题>直线一次追及问题
83、某公司计划采购一批电脑,正好赶上促销期,电脑打9折出售,同样的预算可以比平时多买10台电脑。问该公司的预算在平时能多买多少台电脑?_____
A: 60.B: 70C: 80D: 90
参考答案: D 本题解释:【答案】D。解析:设平时可以购买x台,电脑打折前价格为100,则打折后为90,依题意100x=90(x+10),解得=90。
84、马场有甲、乙、丙、丁四个入口可以提供人进入游玩,如果现在开了甲、乙两个入口,经过了4.5小时游客全部能够进入,如果开乙、丙两个入口,游客3小时能全部进入,如果开丙、丁两个入口,游客3.5小时全部进入。若只打开甲、丁两个入口,则需要几个小时,游客才能全部进入?_____
A: 63/11B: 63/32C: 196/33D: 172/33
参考答案: A 本题解释:【答案】A。解析:设总人数为1,则开甲、乙两个口,1小时能进入2/9人;开乙、丙两个口,1小时能进入1/3人;开丙、丁两个口,一小时能进入2/7人;三种情况同时存在时,一小时能进入的人数为甲口+乙口+乙口+丙口+丙口+丁口=2(乙口+丙口)+甲口+丁口=2/9+1/3+2/7=53/63(人)。又因乙口+丙口=1/3(人),所以甲、丁两口同时开放,1小时进入的人数为11/63人。所以只打开甲、丁两个口,游客全部进入,需要的时间是63/11小时。
85、如果当“张三被录取的概率是1/2,李四被录取的概率是1/4时,命题:要么张三被录取,要么李四被录取” 的概率就是_____
A: 1/4 B: 1/2 C: 3/4D: 4/4
参考答案: B 本题解释:B。【解析】要么张三录取要么李四录取就是2人不能同时录取且至少有一人录取,张三被录取的概率是1/2,李四被录取的概率是1/4,(1/2) ×(3/4)+(1/4) ×(1/2)=3/8+1/8=1/2其中(1/2) ×(3/4)代表张三被录取但李四没被录取的概率,(1/2) ×(1/4)代表张三没被录取但李四被录取的概率。李四被录取的概率为1/4=>没被录取的概率为1-(1/4)=3/4。
86、将进货单价为90元的某商品按100元一个出售时,能卖出500个。这种商品如果每个涨价1元。其销售量就会减少10个,为了获得最大利润,售价应定为_____。
A: 110元B: 120元C: 130元D: 150元
参考答案: B 本题解释:参考答案:B题目详解:设利润为y,售价x,可列方程: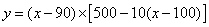 ,解这个二次方程,求得当x=120,y取得最大。所以,选B考查点:数量关系>数学运算>利润利率问题>销售数量和售价反向变化引起的最大利润问题
,解这个二次方程,求得当x=120,y取得最大。所以,选B考查点:数量关系>数学运算>利润利率问题>销售数量和售价反向变化引起的最大利润问题
87、计算:(2+4+6+8+…+2010)-(1+3+5+7+…+2009)=_____。
A: 995B: 1011C: 1111D: 1005
参考答案: D 本题解释:【解析】原式=(2-1)+(4-3)+(6-5)+(8-7)+…+(2010-2009)=1+1+1+1+…+1从2到2010共有1005个偶数,所以原式等于1005个1相加,等于1005,故本题答案为D。
88、张先生向商店订购某种商品80件,每件定价100元。张先生向商店经理说:“如果你肯减价,每减1元,我就多订购4件。”商店经理算了一下,如果减价5%,由于张先生多订购,仍可获得与原来一样多的利润。则这种商品每件的成本是_____。
A: 75元B: 80元C: 85元D: 90元
参考答案: A 本题解释:【解析】A。设成本为x元。减价5%即减去了5元,同样就要多购买4×5=20件,利润相同,即可得到等式(100-x)×80=(95-x)×(80+20),得x=75。
89、 _____
_____
A: AB: BC: CD: D
参考答案: B 本题解释:正确答案是B考点计算问题解析根据尾数法,可知最后两位(即小数点之后)为:01+09+16+64=90,故正确答案为B。
90、已知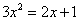 ,则
,则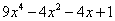 =_____ B: 1C: 2D: 4
=_____ B: 1C: 2D: 4
参考答案: C 本题解释:参考答案:C题目详解:根据题干中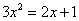 ,可得
,可得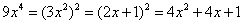 ,那么:
,那么: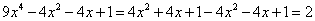 。因此,选C。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
。因此,选C。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
91、有一条400米长的环形跑道。甲、乙两人骑车从A点出发,背向而行。甲的初始速度为1米/秒,乙的初始速度为11米/秒。每当两人相遇。甲的速度就增加1米/秒。乙的速度减少1米/秒。那么当两人以相等的速度相遇时,距离A点多少米?_____
A: 50B: 60C: 75D: 100
参考答案: D 本题解释:D。此题为环形相遇问题,由于每次相遇路程相同,s=400米,速度和均为1+11=12米/秒,因此每次相遇时间都等于400÷12秒。两人速度相等时均为6米/秒,甲骑行总路程为400÷12×(1+2+3+4+5+6)=700米。400×2-700=100米,距离A点100米。
92、三位专家为10幅作品投票,每位专家分别都投出了5票,并且每幅作品都有专家投票。如果三位专家都投票的作品列为A等,两位专家投票的列为B等,仅有一位专家投票的作品列为C等,则下列说法正确的是_____。
A: A等和B等共6幅B: B等和C等共7幅C: A等最多有5幅D: A等比C等少5幅
参考答案: D 本题解释:正确答案是D考点不定方程问题解析解析1:分别以等级代表其数量,根据题意可得A+B+C=10……①;3A+2B+C=15……②②-①×2可得:C-A=5,因此正确答案为D。解析2:代入选项法。根据题意可得A+B+C=10……①;3A+2B+C=15……②此时有3个未知量,只有2个方程,典型的不定方程问题。将选项代入,依次验证是否成立即可。以选项A为例,若选项A正确,则有:A+B=6。到此得到第三个方程,便可求解此方程组,得C=4,A=-1,B=7。故排除A。类似的方法可排除选项B、C。故正确答案为D。解析3:根据题意可得A+B+C=10……①;3A+2B+C=15……②由②-①消去C,可得2A+B=5。由于A、B、C均为非负整数,由此可知0≤2A≤5,因此A只能取值0、1、2。依次代回,可得A、B、C的可能取值为0、5、5;1、3、6;2、1、7三种情形,只有选项D上述三组数据都符合。故正确答案为D。解析4:根据题意可得A+B+C=10……①;3A+2B+C=15……②对不定方程而言,往往不能得到唯一的一组解。但从选项容易看出,只要求出其中一组解即可验证不符合的选项,将其排除掉即可。因此令A=0,发现B=5、C=5,符合非负整数要求。此时可迅速排除前两个选项,而选项C显然错误。故正确答案为D。
93、一种溶液,蒸发掉一定量的水后,溶液的浓度为10%;再蒸发掉同样多的水后,溶液的浓度变为12%;第三次蒸发掉同样多的水后,溶液的浓度将变为多少?_____
A: 14%B: 17%C: 16%D: 15%
参考答案: D 本题解释:正确答案是D考点浓度问题解析在蒸发的过程中,溶液的量发生变化,但其中溶质保持不变,因此将溶质作为解题突破口,给溶质赋值。为方便后面的计算,设其溶质为60,则可知其浓度在10%时,溶液量为600,其浓度在12%时,溶液量为500。这说明在变化过程中蒸发掉了水为100。因此第三次蒸发同样多的水后,溶液还剩400,故其浓度为15%。故正确答案为D。标签赋值思想
94、一件工作甲先做6小时,乙接着做12小时可以完成。甲先做8小时,乙接着做6小时也可以完成。如果甲先做3小时后,再由乙接着做,还需要多少小时完成? _____
A: 16B: 18C: 21D: 24
参考答案: C 本题解释:C【解析】设甲、乙两人每小时的工作量x、y,可列方程6x+12y=18x+6y=1 解得x=110y=130,甲先做了110×3,工作还剩1-310=710,故乙还需要710÷130=21 小时。故选C。
95、在一个长16米、宽12米、高8米的库房中最多可以装下多少只长4市尺、宽3市尺、高2市尺的箱子?_____
A: 1564B: 1728C: 1686D: 1835
参考答案: B 本题解释:参考答案:B题目详解:根据公式1米=3市尺先进行单位换算,库房的体积为: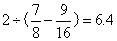 能放箱子的个数为:
能放箱子的个数为: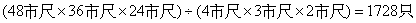 。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
96、有3个企业共订阅300份《经济周刊》杂志,每个企业至少订99份,最多订101份,问一共有多少种不同的订法? _____
A: 6B: 7C: 8D: 9
参考答案: B 本题解释:B。【解析】份数的选择有99,100,101或100,100,100,则第一种选择有A33=6种订法,6+1=7
97、某企业实行计件工资报酬,加工一件合格的得4元;不合格的不计报酬且每件扣除12元。某员工一个月价格1000件,得3600元报酬。该员工这个月价格产品的合格率是多少?_____
A: 96%B: 96.5%C: 97.5%D: 98%
参考答案: C 本题解释:正确答案:C解析:本题考查鸡兔同笼问题。每加工一件不合格产品,要损失4+12=16元,假设全部合格,则应得4×1000元,与所得的3600元相差4000-3600=400元,所以一共有400÷16=25件不合格,合格率为(1000-25)÷l000=97.5%。故答案为C。
98、(山东行测真题)共有920个玩具交给两个车间制作完成、已知甲车间每个人能够完成17个,乙车间每个人能够完成23个,现已知甲、乙两车间共有四十多人,问甲车间比乙车间多多少人?_____ B: 1C: 2D: -2
参考答案: A 本题解释:参考答案:A题目详解:设甲车间有x人,乙车间有y人,则:17x+23y=920;23y和920都能被23整除:则l7x能被23整除,而17和23互质,则x能被23整除;而两个车间人数为四十多人,则x=0、23或46:若x=0,则y=40,x+y=40,舍去;若x=23,则y=23,x+y=46,满足题意,此时x-y=0,选择A;若x=46,则x=6,x+y=52,舍去。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>不定方程问题>二元一次不定方程
99、火车驶过长900米的铁路桥,从车头上桥到车尾离桥共用1分25秒,紧接着列车又穿过一条长1800米的隧道,从车头进隧道到车尾离开隧道用了2分40秒,则火车车身长为_____。
A: 120米B: 100米C: 80米D: 90米
参考答案: A 本题解释:参考答案:A题目详解:应用方程法:由于火车速度相同,设车身长度为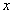 米;从车头上桥到车尾离桥火车行驶距离为:
米;从车头上桥到车尾离桥火车行驶距离为: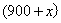 米;从车头进遂道到车尾离开遂道行驶距离为:
米;从车头进遂道到车尾离开遂道行驶距离为: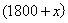 米;列方程:
米;列方程: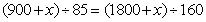 ,解
,解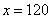 米。所以,选A。考查点:数量关系>数学运算>行程问题>初等行程问题
米。所以,选A。考查点:数量关系>数学运算>行程问题>初等行程问题
100、某单位有职工15人,其中业务人员9人。现要从整个单位选出3人参加培训,要求其中业务人员的人数不数少于非法业务人员的人数。问有多少种不同的选人方法?_____
A: 156B: 216C: 240D: 300
参考答案: D 本题解释:正确答案是D,全站数据:本题共被作答1次,正确率为100.00%解析按照业务员的数量进行分类:第一类:业务员3人,非业务0人,则从9个业务员人中选3人,C(3,9)=84种;第二类:业务员2人,非业务1人。则先从9个业务员里面选2人,C(2,9)=36种,再从6个非业务员里面选1人,C(1,6)=6种,两者相乘等于216种。最后,将两类进行求和得到300种。故正确答案为D。速解本题考查排列组合类题目的重点知识点--分类讨论,只要找到关键分类点”业务人员数”,进行分类计算,即可得到结果。考点排列组合问题标签分类分步笔记编辑笔记