1、甲乙两人从相距1350米的地方,以相同的速度相对行走,两人在出发点分别放下1个标志物。再前进10米后放下3个标志物。前进10米放下5个标志物,再前进10米放下7个标志物,以此类推。当两个相遇时,一共放下了几个标志物?_____
A: 4489B: 4624C: 8978D: 9248
参考答案: D 本题解释:正确答案是D考点数列问题解析以10米为间隔,可知1350米的路程被分成135个间隔,因此共有136个放标志物的点,按甲乙平分为两组,每组为68个点,故甲或乙最后均放置135个标志物。由求和公式可知总数为(1+135)÷2×68×2=9248。因此正确答案为D。注:等差数列求和公式,和=(首项+末项)×项数÷2秒杀技易知全程被分为135个间隔,从而得出每组放置标志物的点为偶数,注意到每次放下标志物都为奇数,从而可知每组的标志物总数必然为偶数。又考虑到甲乙两组是相同的,而选项中C、D分别为A、B的两倍,而A、B中B为偶数,故可猜测B为一人放下的标志物数,而D为答案。标签猜题技巧
2、(2004国家,第36题)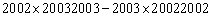 的值是_____。
的值是_____。
A: 60C: 70D: 80
参考答案: B 本题解释:参考答案:B题目详解:应用因式分解法:将进行乘法运算的数拆分为两数的乘积形式;再利用乘法交换律进行计算;原式=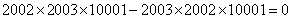 ;所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
;所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
3、甲、乙两车运一堆货物。若单独运,则甲车运的次数比乙车少5次;如果两车合运,那么各运6次就能运完,甲车单独运完这堆货物需要多少次_____
A: 9B: 10C: 13D: 15
参考答案: B 本题解释:【答案】B。解析:工程问题。设甲单独需要x,则乙单独需要x+5,依题意有1/x+1/(x+5)=1/6,解得x=10。
4、一袋白糖,第一次用去0.3斤,第二次用去余下的3/4,这时袋内还有白糖0.2斤,该袋糖原有多少斤?_____
A: 1.1B: 0.5C: 1.5D: 2
参考答案: A 本题解释: A 【解析】0.2÷(1-3/4)+0.3=1.1。
5、(2009天津、湖北、陕西联考,第95题)有4支队伍进行4项体育比赛,每项比赛的第一、第二、第三、第四名分别得到5,3,2,1分,每队的4项比赛的得分之和算作总分,如果已知各队的总分不相同,并且A队获得了三项比赛的第一名,问总分最少的队伍最多得多少分?_____
A: 7B: 8C: 9D: 10
参考答案: B 本题解释:参考答案:B题目详解:本题需要运用“构造法”和“极端法”。由于题目求“总分最少的队伍最多得多少分”,我们需要让各队的得分尽可能的平均。每项比赛产生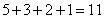 分,4项比赛一共产生
分,4项比赛一共产生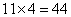 分,最终平均每人得到
分,最终平均每人得到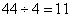 分。A已经获得了
分。A已经获得了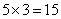 分,超过平均分,需要A最后=场比赛得尽量少的分,即1分,那么剩下3个人将得到
分,超过平均分,需要A最后=场比赛得尽量少的分,即1分,那么剩下3个人将得到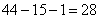 分。要让剩下三个人比分尽可能的平均,可以构造
分。要让剩下三个人比分尽可能的平均,可以构造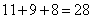 ,在这个条件下,部分最少的队伍可以得到最多的分数,即8分。下面我们构造这种比赛的情形:
,在这个条件下,部分最少的队伍可以得到最多的分数,即8分。下面我们构造这种比赛的情形: 考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
6、一个小数的小数点向右移动一位与向左移动一位所得的两数之和为1214.222,这个小数是多少?_____
A: 118.82B: 119.22C: 119.82D: 120.22
参考答案: D 本题解释:参考答案 题目详解:设原来的数为x:小数点向右移动一位,即原来的数乘以10;小数点向左移动一位,即原来的数乘以0.1;两数之和为:l0x+0.lx=1214.222;解得x=120.22;所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的排列与位数关系
题目详解:设原来的数为x:小数点向右移动一位,即原来的数乘以10;小数点向左移动一位,即原来的数乘以0.1;两数之和为:l0x+0.lx=1214.222;解得x=120.22;所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的排列与位数关系
7、一个圆形牧场面积为3平方公里,牧民骑马以每小时18公里的速度围着牧场外沿巡视一圈,约需多少分钟?_____
A: 12B: 18C: 20D: 24
参考答案: C 本题解释:正确答案是C考点几何问题解析
8、某次投资活动中在三个箱子中均放有红、黄、绿、蓝、紫、橙、白、黑8种颜色的球各一个。奖励规则如下:从三个箱子分别摸出一个球,摸出的3个球均为红球得一等奖,摸出的3个球至少有一个绿球得二等奖,摸出的3个球均为彩色球(黑、白除外)得三等奖,那么不中奖的概率是_____。
A: 0—25%之间B: 25—50%之间C: 50—75%之间D: 75—100%之间
参考答案: B 本题解释:正确答案是B考点概率问题解析
9、甲容器有浓度为3%的盐水190克,乙容器中有浓度为9%的盐水若干克,从乙取出210克盐水倒入甲,甲容器中的盐水的浓度是多少? _____
A: 5.45%B: 6.15%C: 7.35%D: 5.95%
参考答案: B 本题解释: B。根据两溶液混合公式可得,3%×190+9%×210=(190+210)×C,解得C=6.15%。故正确答案为B。
10、西南赛区四支球队为了争夺小组第一名而进行小组循环赛,已知小马队已比赛了3场,小熊队已比赛了2场,小龙队已比赛了1场,问小牛队比赛了几场_____
A: 3B: 2C: 1
参考答案: B 本题解释:参考答案:B题目详解:小马队已比赛了3场:说明小马队和小熊队、小龙队、小牛队各打了1场;小龙队已比赛了1场:说明小龙队只和小马队比赛了1场;小熊队已比赛了2场:因为和小马队比赛了1场,所以还有1场比赛。因为小龙队只和小马队比赛过,所以小熊队只能和小牛队进行比赛。因此小牛队比赛了2场,分别是和小马队、小熊队进行的比赛。所以,选B。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
11、两个游泳运动员在长为30米的游泳池内来回游泳,甲的速度为1米/秒,乙为0.6米/秒,他们分别从两端出发,来回共游了5分钟。转身时间不计,这段时间内他们相遇多少次?_____
A: 120B: 1440C: 2160D: 2880
参考答案: C 本题解释:参考答案:C题目详解:根据题意,可知:第一次相遇,甲、乙总共走了2个全程,第二次相遇,甲、乙总共走了4个全程,乙比甲快,相遇又在P点。所以可以推出:从第一次相遇到第二次相遇,甲从第一个P点到第二个P点,路程正好是第一次的路程,则P到A点的路程为P到B点路程的2倍。假设一个全程为3份,第一次相遇甲走了2份,乙走了4份;第二次相遇,乙正好走了1份到B地,又返回走了1份;2个全程里乙走了:(540÷3)×4=180×4=720千米,乙总共走了:720×3=2160千米。所以,选C考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
12、现有一种预防禽流感药物配置成的甲、乙两种不同浓度的消毒溶液。若从甲中取2100克,乙中取700克混合而成的消毒浓度为3%;若从甲中取900克,乙中取2700克,则混合而成的溶液的浓度为5%。则甲、乙两种消毒溶液的浓度分别为_____。
A: 3%6%B: 3%4%C: 2%6%D: 4%6%
参考答案: C 本题解释:【答案】C。解析:设两种溶液的浓度分别为a、b,则可列方程2100a+700b=(2100+700)×3%,900a+2700b=(900+2700)×5%,解得a=2%,仅C选项符合,故正确答案为C。老师点睛:甲中去2100克,乙中取700克混合而成的消毒溶液浓度为3%,则甲、乙两溶液的浓度必然是一个比3%大,一个比3%小,只有C选项符合,故正确答案为C。
13、(2009河北选调,第49题)一个盒子里有8个红球、6个蓝球、4个绿球、2个白球,如果闭上眼睛,从盒子中摸球,每次只许摸一个球,至少要摸出几个球,才能保证摸出的这几个球中至少有两个颜色相同?_____
A: 4B: 5C: 6D: 8
参考答案: B 本题解释:参考答案:B题目详解:题目要求“保证摸出的球至少有两个颜色相同”,最不利的情况就是“总是摸出颜色不相同的球”,总共只有4种颜色,可以摸出4个颜色不相同的球,因此摸5个就能保证摸出的球有两个颜色相同。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1
14、从0,1,2,7,9五个数字中任选四个不重复的数字,组成的最大四位数和最小四位数的差是_____。
A: 8442B: 8694 C: 8740D: 9694
参考答案: B 本题解释:答案:B。由题意可得:最大的四位数为9721,最小的四位数为1027,故两者的差是9721-1027=8694。
15、某数除以11余8,除以13余10,除以17余12,那么这个数的最小可能值是_____
A: 140B: 569C: 712D: 998
参考答案: D 本题解释:D。选项中只有998加上3能整除11和13,加上5能整除17。
16、商场的自动扶梯以匀速由下往上行驶,两个孩子嫌扶梯走得太慢,于是在行驶的扶梯上,男孩每秒钟向上走2个梯级,女孩每2秒钟向上走3个梯级。结果男孩用40秒钟到达,女孩用50秒钟到达。则当该扶梯静止时,可看到的扶梯梯级有_____。
A: 80级 B: 100级 C: 120级 D: 140级
参考答案: B 本题解释:B。【解析】男孩所走的台阶数为40×2=80,女孩所走的台阶数为50/2×3=75,那么电梯的速度就应该为(80-75)/(50-40)=0.5,电梯所经过的台阶就为40×0.5=20, 电梯经过的台阶加上男孩经过的台阶,就是电梯的台阶数,即100级。
17、为节约用水,某市决定用水收费实行超额超收,标准用水量以内每吨2.5元,超过标准的部分加倍收费。某用户某月用水15吨,交水费62.5元,若该用户下个月用水12吨,则应交水费多少钱?_____
A: 42.5元B: 47.5元C: 50元D: 55元
参考答案: B 本题解释:参考答案:B题目详解:如果该用户15吨水全部都交5元钱/吨,则他应当交75元水费,比实际缴纳额少了12.5元。少缴纳的12.5元是因为未超出标准用水量的部分,每吨缴纳2.5元,因此标准水量为:12.5÷2.5=5吨因此,无论是15吨或是12吨,都已经超过了标准水量,所以用水12吨时,应当比用水15吨少缴纳:3×5=15元因此,用水量为12吨时,应缴纳水费:62.5-15=47.5元。所以,选B。考查点:数量关系>数学运算>特殊情境问题>分段计算问题
18、甲、乙两个容器均有50厘米深,底面积之比为5:4,甲容器水深9厘米,乙容器水深5厘米,再往两个容器各注入同样多的水,直到水深相等,这时两容器的水深是_____。
A: 20厘米B: 25厘米C: 30厘米D: 35厘米
参考答案: B 本题解释:正确答案是B考点几何问题解析设注入水后的水深为y厘米,则根据注入水同样多,可知(y-9)×5=(y-5)×4,解得y=25,故正确答案为B。
19、我们知道,一个正方形可以剪成4个小正方形,那么一个正方形能否剪成11个正方形,能否剪成13个正方形(大小不一定相同)?_____
A: 前者能,后者不能B: 前者不能,后者能C: 两个都能D: 两个都不能
参考答案: C 本题解释:【答案】C。
20、有41个学生要坐船过河,渡口处只有一只能载4人的小船(无船工),他们要全部渡过河去,至少要使用这只小船渡河多少次?_____
A: 23B: 24C: 27D: 26
参考答案: C 本题解释:【答案】C。解析:套用公式,过河次数=(41-1)/(4-1)=13.33,过河次数为整数,13<13.33<14,要使所有人都过河,只能取14。所求次数为单程次数,来回总共14×2-1=27次(最后一次过河不再返回)。故正确答案为C。公式:过河问题中每次过河都需要有一个人将船划回来,而最后一次过河不再需要划回来。N个人过河,船最多载M人,则过河次数为(N-1)/(M-1)。过河次数指单程次数,注意最后一次过河不需要人划回来,总次数=单程次数×2-1。
21、某人同时购买2年期、5年期和10年期三种国债,投资额的比为5:3:2。后又以与前次相同的投资总额全部购买5年期国债,则此人两次对5年期国债的投资额占两次总投资的比例的_____。
A: 3/5B: 7/10C: 3/4D: 13/20
参考答案: D
22、一条路上依次有A、B、C三个站点,加油站M恰好位于A、C的中点,加油站N恰好位于B、C的中点,若想知道M和N两个加油站之间的距离,只需知道哪两点之间的距离?_____
A: B和CB: C和NC: A和MD: A和B
参考答案: D 本题解释:正确答案是D考点几何问题解析画图分析可知,MN=AC/2-BC/2=(AC-BC)/2=AB/2,则只需知道AB的距离,就可知道MN的距离。故正确答案为D。
23、现有A、B、C三桶油,先把A的1/3倒入B桶,再把B桶的1/4倒入C桶,最后把C桶的1/10倒入A桶,经这样操作后,三桶油各为90升。问A桶原来有油多少升?_____
A: 90B: 96C: 105D: 120
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析三桶油各为90升。先看第三步:把C桶的1/10倒入A桶之后都是90升,那么倒之前C桶是100升,A是80升;再看第一步:把A桶的1/3倒入B桶之后A还有80升,那么A原来就有120升。故正确答案为D。
24、计算:(1+12)×(1-12)×(1+13)×(1-13)×…×(1+199)×(1-199)的值为_____。
A: 1C: 50/101D: 50/99
参考答案: D 本题解释:D[解析]原式=(1+1/2)×(1+1/3)×…×(1+1/99)×(1-1/2)×(1-1/3)×…×(1-1/99)=(3/2×4/3×5/4×…×99/98×100/99)×(1/2×2/3×3/4×…×97/98×98/99)=100/2×1/99=50/99因此,本题正确答案为D。
25、我们知道,一个正方形可以剪成4个小正方形,那么一个正方形能否剪成11个正方形,能否剪成13个正方形(大小不一定相同)?_____
A: 前者能,后者不能B: 前者不能,后者能C: 两个都能D: 两个都不能
参考答案: C 本题解释:正确答案是C考点几何问题解析 标签画图分析
标签画图分析
26、现在时间为4点13分,此时时针与分针成什么角度?_____
A: 30度B: 45度C: 90度D: 120度
参考答案: B 本题解释:正确答案是B考点钟表问题解析解析1:本题属于钟表问题。把钟面看做圆形,12点为原点。4点13分时针在4和5之间,则120<时针的度数<150,分针的度数=360×13/60=78。可知时针和分针所成的角度x满足120-78<X<150-78。42<X<72,在这个范围内的只有B项45度。故正确答案为B。<p>解析2:把钟面看做圆形,12点为原点。看成追击问题。时针每分钟转的度数为360×1/12×1/60=0.5。分针每分钟转的度数为360×1/60=6。4点13分两针的夹角为120+0.5×13-6×13=48.5≈45。故正确答案为B。
27、一艘轮船在两码头之间航行。如果顺水航行需8小时,逆水航行需11小时。已知水速为每小时3千米,那么这艘轮船每小时行驶多少千米,两码头之间的距离是多少千米_____
A: 19,176B: 18,184C: 19,190D: 18,168
参考答案: A 本题解释:【解析】A。顺水航行8小时比逆水航行8小时多航行了(千米),这是逆水航行11-8=3(小时)航行的路程,所以逆水速度是(千米/小时),轮船的速度为16+3=19(千米/小时),两,码头之间的距离为(千米)。
28、“红星”啤酒开展“7个空瓶换l瓶啤酒”的优惠促销活动。现在已知张先生在活动促销期问共喝掉347瓶“红星”啤酒,问张先生最少用钱买了多少瓶啤酒?_____
A: 296B: 298C: 300D: 302
参考答案: B 本题解释:由题可知,6个空瓶可以换一个瓶子里面的啤酒,298÷6=49……4,只有49+298=347。
29、甲、乙两个厂生产同一种玩具,甲厂生产的玩具数量每天保持不变,乙厂生产的玩具数量每天增加一倍,已知第一天甲、乙两个厂生产的玩具总数是98件,第二天甲、乙两个厂生产的玩具总数是106件。那么乙厂生产的玩具数量第一次超过甲厂生产的玩具数量是在第几天?_____
A: 3B: 4C: 5D: 7
参考答案: C 本题解释:正确答案是C考点不等式分析问题解析
30、甲某打电话时忘记了对方电话号码最后一位数字,但记得这个数字不是"0"。甲某尝试用其他数字代替最后一位数字,恰好第二次尝试成功的概率是_____。
A: 1/9B: 1/8C: 1/7D: 2/9
参考答案: A 本题解释:正确答案是A考点概率问题解析最后一个数字不是0,共有9种选择。要求恰好第二次尝试成功,则第一次尝试失败,概率为8/9,第二次更换数字成功,概率为1/8,因此恰好第二次尝试成功的概率为8/9×1/8=1/9。故正确答案为A。秒杀技根据不放回摸球模型,恰好第二次尝试成功的概率与恰好第一次成功的概率相同,因此该概率值为1/9。故正确答案为A。
31、一家公司2006年的月累计利润y(单位:万元)与月份x的变化关系如下表所示: 则该公司2006年的月平均利润是_____万元。
则该公司2006年的月平均利润是_____万元。
A: 15B: 16C: 21D: 30
参考答案: C 本题解释:正确答案是C解析把x=1和x=2代入可得1+b+c=21,4+2b+c=32,联立解得b=8,c=12。当x=12时,y=12×12+8×12+12=252万元,月平均利润为252÷12=21万元,故正确答案为C。考点经济利润问题
32、三位采购员定期去某市场采购,小王每隔9天去一次,大刘每隔6天去一次,老杨每隔7天去一次,三人星期二第一次在这里碰面,下次相会将在星期几?_____
A: 星期一B: 星期五C: 星期二D: 星期四
参考答案: C 本题解释:C解析:此题乍看上去是求9,6,7的最小公倍数的问题,但这里有一个关键词,即“每隔”,“每隔9天”也即“每10天”,所以此题实际上是求10,7,8的最小公倍数。既然该公倍数是7的倍数,那么肯定下次相遇也是星期二。(10,7,8的最小公倍数是5×2×7×4=280。280÷7=40,所以下次相遇肯定还是星期二。)
33、下列哪项能被11整除? _____
A: 937845678B: 235789453C: 436728839D: 867392267
参考答案: A 本题解释:A【解析】9+7+4+6+8=343+8+5+7=2334-23=11所以,答案是A。
34、若 ,
, ,则X和Y的大小关系是_____。
,则X和Y的大小关系是_____。
A: 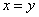 B:
B:  C:
C:  D: 不确定
D: 不确定
参考答案: B 本题解释:参考答案:B题目详解:解法一:令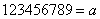 ,则:
,则: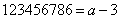 ,
,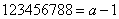 ,
,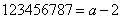 ;故:
;故: ,则
,则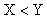 。所以,选B解法二:X=(123456788+1)×(123456787-1)=123456788×123456787-123456788+123456787-1=123456788×123456787-2所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
。所以,选B解法二:X=(123456788+1)×(123456787-1)=123456788×123456787-123456788+123456787-1=123456788×123456787-2所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
35、某次数学竞赛设一、二等奖。已知(1)甲、乙两校获奖的人数比为 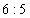 。(2)甲、乙两校获二等奖的人数总和占两校获奖人数总和的
。(2)甲、乙两校获二等奖的人数总和占两校获奖人数总和的 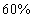 。(3)甲、乙两校获二等奖的人数之比为
。(3)甲、乙两校获二等奖的人数之比为 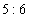 。问甲校获二等奖的人数占该校获奖总人数的百分数是几?_____
。问甲校获二等奖的人数占该校获奖总人数的百分数是几?_____
A: 20B: 30C: 50D: 60
参考答案: C 本题解释:参考答案:C题目详解:已知甲、乙两校获二等奖的人数之比为5:6,那么设甲获二等奖的人数为5份,乙为6份。因为二等奖的人数占两校人数总和的60%,那么甲校获二等奖人数占总数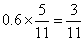 又因为甲、乙两学校获奖人数比为6:5,所以设总人数为11份,甲得奖的占其中6份可知甲校获二等奖者占该校获奖总人数的
又因为甲、乙两学校获奖人数比为6:5,所以设总人数为11份,甲得奖的占其中6份可知甲校获二等奖者占该校获奖总人数的 。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
36、有一批长度分别为3、4、5、6和7厘米的细木条,它们的数量足够多,从中适当选取3根木条作为三角形的三条边,可能围成多少个不同的三角形?_____
A: 25个B: 28个C: 30个D: 32个
参考答案: D 本题解释:正确答案是D考点几何问题解析 标签分类分步
标签分类分步
37、有四个数,其中每三个数的和分别是45,46,49,52,那么这四个数中最小的一个数是多少?_____
A: 12B: 18C: 36D: 45
参考答案: A 本题解释:【答案】A。解析:将45、46、49、52直接相加,可知其值等于原来四个数之和的3倍,于是可知原四个数字之和为:(45+46+49+52)÷3=64,因此最小的数为:64-52=12,故选择A选项。老师点睛:45为最小的三个数之和,平均数为15,则最小的数必然小于15,仅A符合。
38、烙饼需要烙它的正、反面,如果烙熟一张饼的正、反面各用去3分钟,那么用一次可容下2张饼的锅来烙21张饼,至少需要多少分钟?_____
A: 50B: 59C: 63D: 71
参考答案: C 本题解释:参考答案:C题目详解:先将两张饼同时放人锅内一起烙,3分钟后两张饼都熟了一面.这时取出一张,第二张翻个身,再放人第三张,又烙了3分钟,第二张已经烙熟取出来,第三张翻个身,再将第一张放人烙另一面,再烙3分钟,锅内的两张饼均已烙熟。这样烙3张饼,用时9分钟。所以烙21张饼,至少用去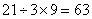 分钟。考查点:数量关系>数学运算>统筹问题>时间统筹问题
分钟。考查点:数量关系>数学运算>统筹问题>时间统筹问题
39、一队战士排成三层空心方阵多出9人,如果在空心部分再增加一层,又差7人,问这队战士共有多少人?_____
A: 121B: 81C: 96D: 105
参考答案: D 本题解释:D[解一]由题意可得空心方阵再往里一层的总人数是:9+7=16(人),每边人数为:16÷4+1=5(人);所以3层空心方阵最外层每边人数为:5+2×3=11(人),总人数为:(11-3)×3×4=96(人);这队战士的总人数是:96+9=105(人)。[解二]相邻两层的人数之差为8人,最里层的人数为9+7+8=24人,次里层为24+8=32人,最外层为32+8=40人,所以总人数为24+32+40+9=105人。
40、四个相邻质数之积为17017,他们的和为_____
A: 48B: 52C: 61D: 72
参考答案: A 本题解释:答案:A【解析】17017分解因数为17×13×11×7,他们的和为48。
41、(2008广东,第13题)60个人上身着白上衣或黑上衣,下身着蓝裤子或黑裤子。其中有12个人穿白上衣蓝裤子,有34个人穿黑裤子,有29个人穿黑上衣,求身着黑裤子黑上衣多少人?_____
A: 13B: 14C: 15D: 20
参考答案: C 本题解释:参考答案:C题目详解:解法一:根据题意,设穿黑裤子黑上衣的人数有x人。根据公式“黑裤子数+黑上衣数-黑裤子黑上衣数=总数-白衣服蓝裤子数”可得: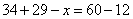 ,解得
,解得 。所以,选C。解法二:根据题意,设上衣分别为1、2,裤子分别为3、4。总共4种穿衣的情况:
。所以,选C。解法二:根据题意,设上衣分别为1、2,裤子分别为3、4。总共4种穿衣的情况: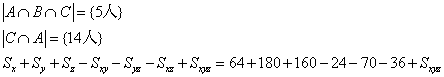 ;
;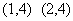 ;又因为:
;又因为: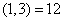 ,
,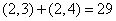 ,
,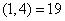 ,
, ;所以,可得:
;所以,可得: 所以,选C。解法三:根据题意,可知:60名运动员中有34人穿黑裤子,则剩下的60-34=26人穿蓝色裤子。而穿蓝色裤子的26人中有12人穿白上衣,那么剩下的26-12=14人穿黑上衣且蓝裤子又穿黑上衣的29人中有14人穿蓝裤子,那么剩下的人穿黑裤子且黑上衣,有29-14=15人。如图所示:
所以,选C。解法三:根据题意,可知:60名运动员中有34人穿黑裤子,则剩下的60-34=26人穿蓝色裤子。而穿蓝色裤子的26人中有12人穿白上衣,那么剩下的26-12=14人穿黑上衣且蓝裤子又穿黑上衣的29人中有14人穿蓝裤子,那么剩下的人穿黑裤子且黑上衣,有29-14=15人。如图所示: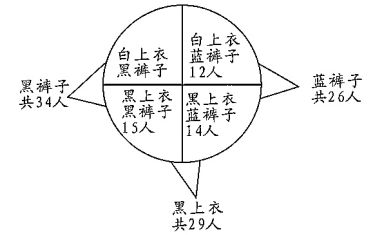 所以,选C。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
所以,选C。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
42、三个圆的半径都是5厘米,三个圆两两相交于圆心。求阴影部分的面积之和。_____ 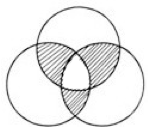
A: 29.25平方厘米B: 33.25平方厘米C: 39.25平方厘米D: 35.35平方厘米
参考答案: C 本题解释:正确答案是C考点几何问题解析使用割补法可知阴影部分的面积相当于半个圆的面积,则可得25π÷2=25×3.14÷2=39.25。故正确答案为C。
43、某单位订阅了30份学习材料发放给3个部门,每个部门至少发放9份材料。问一共有多少种不同的发放方法?_____
A: 7B: 9C: 10D: 12
参考答案: C 本题解释:正确答案是C考点排列组合问题解析 因此正确答案为C。
因此正确答案为C。
44、计算19961997×19971996-19961996×19971997的值是_____。
A: 0B: 1C: 10000D: 100
参考答案: C 本题解释:C【解析】原式=(19961996+1)×19971996-19961996×(19971996+1)=19971996-19961996=10000
45、已知猫跑5步的路程与狗跑3步的路程相同,猫跑7步的路程与兔跑5步的路程相同。而猫跑3步的时间与狗跑5步的时间相同,猫跑5步的时间与兔跑7步的时间相同。猫、狗、兔沿着周长为300米的圆形跑道,同时同向同地出发,问当它们出发后第一次相遇时狗跑了多少路程? _____
A: 8437.5米B: 23437.5米C: 16537.5米D: 25337.5米
参考答案: B 本题解释:【解析】B。解析:猫和狗的速度比为 ;猫和兔的速度比为
;猫和兔的速度比为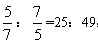 ,可得猫、狗和兔的速度比为225:625:441。猫和狗第一次相遇的时间为300÷(625-225)=3/4;猫和兔第一次相遇的时间为300÷(441-225)=25/18 ,可得猫、狗和兔第一次相遇的时间为3/4和25/18的最小公倍数75/2,故相遇时狗跑了625×75/2=23437.5米。
,可得猫、狗和兔的速度比为225:625:441。猫和狗第一次相遇的时间为300÷(625-225)=3/4;猫和兔第一次相遇的时间为300÷(441-225)=25/18 ,可得猫、狗和兔第一次相遇的时间为3/4和25/18的最小公倍数75/2,故相遇时狗跑了625×75/2=23437.5米。
46、小明通常总是步行上学,有一天他想锻炼身体,前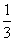 路程快跑,速度是步行速度的4倍,后一段的路程慢跑。速度是步行速度的2倍。这样小明比平时早35分钟到校,小明步行上学需要多少分钟?_____
路程快跑,速度是步行速度的4倍,后一段的路程慢跑。速度是步行速度的2倍。这样小明比平时早35分钟到校,小明步行上学需要多少分钟?_____
A: 60B: 45C: 120D: 90
参考答案: A 本题解释:参考答案:A题目详解:设路程是 ,步行速度是
,步行速度是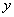 :小明步行上学需要
:小明步行上学需要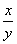 分钟;根据题意,列等式得:
分钟;根据题意,列等式得: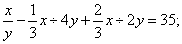 得到
得到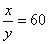 。所以,选A。考查点:数量关系>数学运算>行程问题>初等行程问题
。所以,选A。考查点:数量关系>数学运算>行程问题>初等行程问题
47、(2006北京社招,第18题)有-水池,池底有泉水不断涌出,要想把水池的水抽干,l0台抽水机需抽8小时,8台抽水机需抽12小时,如果用6台抽水机,那么需抽多少小时?_____
A: 16B: 20C: 24D: 28
参考答案: C 本题解释:参考答案:C题目详解:依题意:设泉水的原有存量为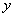 ;单位时间进水量即自然增长速度为
;单位时间进水量即自然增长速度为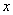 ;存量完全消失所消耗的时间
;存量完全消失所消耗的时间 为所求;代入公式:
为所求;代入公式: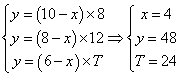 所以,选C。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
所以,选C。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
48、有一本畅销书,今年每册书的成本比去年增加了10%,因此每册书的利润下降了20%,但是今年的销量比去年增加了70%。则今年销售该畅销书的总利润比去年增加了_____。
A: 36%B: 25%C: 20%D: 15%
参考答案: A 本题解释:每本书的利润值下降了20%,为原来的0.8,销量增加了70%,为原来的1.7,1.7×0.8=1.36,1.36—1=0.36,即为36%。
49、某公司三名销售人员2011年的销售业绩如下:甲的销售额是乙和丙销售额的1.5倍,甲和乙的销售是丙的销售额的5倍,已知乙的销售额是56万元,问甲的销售额是_____。
A: 140万元B: 144万元C: 98万元D: 112万元
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析由题意,甲=1.5(乙+丙),甲+乙=5丙,将乙=56代入,可得甲=144,丙=40。故答案为B。秒杀技秒杀一:由甲的销售额是乙丙之和的1.5倍,而1.5中含有因子3,因此甲的销售额能被3整除,仅B符合。秒杀二:甲和乙的销售额之和是丙销售额的5倍,因此甲乙销售额之和能够被5整除,其尾数为0或5,在四个选项中仅B符合这一要求。
50、某单位组织党员参加党史、党风廉政建设,科学发展观和业务能力四项培训,要求每名党员参加且只参加其中的两项。无论如何安排,都有至少5名党员参加的培训完全相同,问该单位至少有多少名党员?_____
A: 17B: 21C: 25D: 29
参考答案: C 本题解释:正确答案是C考点抽屉原理问题解析
51、(2006北京社招,第11题)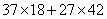 的值是_____。
的值是_____。
A: 1800B: 1850C: 1900D: 2000
参考答案: A 本题解释:参考答案:A题目详解:应用因式分解法: ;
; 考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
52、幼儿园里,老师将一堆桃子分给同学,如果每个同学分3个则余2个,如果每个同学分4个,则有两个同学分不到,该班有多少个同学?_____
A: 10B: 12C: 15D: 18
参考答案: A 本题解释:A【解析】设共有x个同学,由题意得3x+2=4(x-2),解得x=10。
53、一个两位数除以一个一位数,商仍是两位数,余数是8。问:被除数、除数、商以及余数之和是多少?_____
A: 98B: 107C: 114D: 125
参考答案: D 本题解释:【答案】D。解析:猜证结合的98÷10=9余8,10+98+9+8=125。
54、龟兔赛跑,全程5.2千米,兔子每小时跑20千米,乌龟每小时跑3千米。乌龟不停地跑,但兔子却边跑边玩,它先跑一分钟,然后玩十五分钟,又跑二分钟,然后玩十五分钟,又跑三分钟,然后玩十五分钟,……,那么先到达终点的比后到达终点的快多少分钟?_____
A: 104分钟B: 90.6分钟C: 15.6分钟D: 13.4分钟
参考答案: D 本题解释:正确答案是D考点趣味数学问题解析乌龟到达终点所需时间为:5.2÷3×60=104分钟,兔子如果不休息,则需要时间:5.2÷20×60=15.6分钟。而实际兔子休息的规律为每跑1、2、3、······分钟后,休息15分钟,因为15.6=1+2+3+4+5+0.6,所以兔子总共休息的时间为:15×5=75分钟,即兔子跑到终点所需时间为:15.6+75=90.6分钟,因此兔子到达终点比乌龟快:104-90.6=13.4分钟,故正确答案为D。
55、把1~200这200个自然数中,既不是3的倍数,又不是5的倍数,从小到大排成一排,那么第100个是几?_____
A: 193B: 187C: 123D: 40
参考答案: B 本题解释:B【解析】 从1至200的自然数中是3的倍数的数有66个,是5的倍数的数有40个,而既是3又是5的倍数的数有13个。所以从1至200的自然数中是3或5的倍数的数有(66+40-13)=93个,所以从1至200的这200个自然数中,既不是3又不是5的倍数的数有(200-93)=107个。现在要求第100个,即倒数第8个。将它从大到小列出:199、197、196、194、193、191、188、187……即从小到大排列第100个是187。故本题选B。
56、如下图,梯形ABCD的对角线AC⊥BD,其中AD=1/2,BC=3,AC=2×4/5,BD=2.1。问梯形ABCD的高AE的值是_____。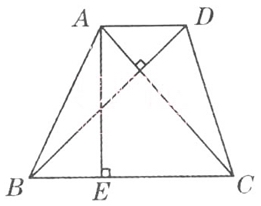
A: 43/24B: 1.72C: 4/252D: 1.81
参考答案: C 本题解释:【解析】由AC×BD=(AD+BC)×AE→AE=42/25。
57、A、B、C三件衬衫的总价格为520元,分别按9.5折,9折,8.75折出售,总价格为474元,A、B两件衬衫的价格比为5﹕4,A、B、C三件衬衫的价格分别是多少元?()
A: 250,200,70B: 200,160,160C: 150,120,250D: 100,80,340
参考答案: B 本题解释:设A,B,C三件衬衫的价格分别为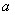 ,
,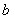 ,
,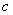 ,则可以列方程组:
,则可以列方程组: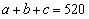 ,
,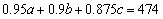 ,
, ,解得
,解得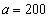 ,
,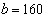 ,
,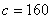 ,所以选B。
,所以选B。
58、100个孩子按1、2、3……依次报数,从报奇数的人中选取k个孩子,他们所报数字之和为1949,问k最大值为多少?_____
A: 43B: 44C: 45D: 46
参考答案: A 本题解释:【答案】A。解析:奇数个奇数的和为奇数,故k的最大值应是奇数,排除B、D;从1开始,45个连续奇数的和是452>1949,排除C,此题答案为A。
59、现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都做错的有4人,则两种实验都做对的有_____。
A: 27人B: 25人C: 19人D: 10人
参考答案: B 本题解释:参考答案:B题目详解:解法一:A={{物理实验做正确的人}};B={{化学实验做正确的人}}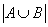 ={{至少做对一种的人数}};
={{至少做对一种的人数}}; ={{两种实验都做对的人}}根据容斥原理可得:
={{两种实验都做对的人}}根据容斥原理可得: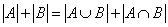 ,代入得:
,代入得: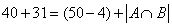 。则
。则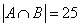 ,所以,选B。解法二:由题意知,两种试验都做错的有4人,则至少做对一种的有46人。而题目已经告知有40人做对物理实验,则说明有6人只做对化学试验。同时有31人作对化学试验,则说明有15人只做对物理实验而做错了化学实验。所以题目的解答为:50-4(全做错)-15(物理对化学错)-6(化学对物理错)=25人。所以,选B。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
,所以,选B。解法二:由题意知,两种试验都做错的有4人,则至少做对一种的有46人。而题目已经告知有40人做对物理实验,则说明有6人只做对化学试验。同时有31人作对化学试验,则说明有15人只做对物理实验而做错了化学实验。所以题目的解答为:50-4(全做错)-15(物理对化学错)-6(化学对物理错)=25人。所以,选B。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
60、(2009浙江,第50题)“红星”啤酒开展“7个空瓶换一瓶啤酒”的优惠促销活动。现在已知张先生在活动促销期间共喝掉347瓶“红星”啤酒,问张先生最少用钱买了多少瓶啤酒?_____
A: 296瓶B: 298瓶C: 300瓶D: 302瓶
参考答案: B 本题解释:参考答案:B题目详解: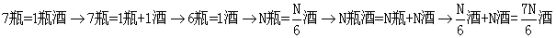 可知
可知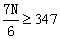 ,解得
,解得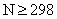 考查点:数量关系>数学运算>统筹问题>空瓶换酒问题
考查点:数量关系>数学运算>统筹问题>空瓶换酒问题
61、水池装有一个排水管和若干个每小时注水量相同的注水管,注水管注水时,排水管同时排水,若用12个注水管注水,8小时可注满水池,若用9个注水管,24小时可注满水,现在用8个注水管注水,那么可用_____注满水池。
A: 12小时B: 36小时C: 48小时D: 72小时
参考答案: D 本题解释:正确答案是D考点牛吃草问题解析设原有水量为N,每小时排水量为Y,可得如下:N=(12-Y)×8=(9-Y)×24,解得N=36,Y=7.5;若用8个注水管,注满时间为t,则有36=(8-7.5)×t,解得t=72小时,故正确答案为D。
62、某商店将定价为6.25元的笔记本降价20%卖出,结果还获成本25%的利润。笔记本的成本为_____。
A: 5元B: 4元C: 3元D: 2元
参考答案: B 本题解释:B【解析】设成本为x元,计算得x=4。
63、气象台测得在S岛正东方向80千米处,一台风中心正以20千米/小时的速度沿北偏西60度的方向匀速移动。若台风中心50千米范围内为影响区域,台风中心移动方向不变、强度不变,该台风对S岛的影响时间约持续_____。
A: 2小时B: 3小时C: 4小时D: 5小时
参考答案: B 本题解释:正确答案是B考点几何问题解析 故正确答案为B。
故正确答案为B。
64、某小学六年级的同学要从10名候选人中投票选举三好学生,规定每位同学必须从这10个人中任选两名,那么至少有_____人参加投票,才能保证必有不少于5个同学投了相同两个候选人的票。
A: 256B: 241C: 209D: 181
参考答案: D 本题解释:【解析】从10人中选2人,共有45种不同的选法。要保证至少有5个同学投了相同两个候选人的票,由抽屉原理知,至少要45×4+1=181人。
65、两排蜂房,一只蜜蜂从左下角的1号蜂房到8号蜂房,假设只向右方(正右或右上或右下)爬行,则不同的走法有_____。
A: 16种B: 18种C: 21种D: 24种
参考答案: C 本题解释: 
66、某盒灯泡中有3只次品和6只正品(每只均可区分),测试员每次取出一只进行测试,直到3只次品全部测出为止。假如第三只次品在第六次测试时被发现,那么不同的测试情况共有多少种?_____
A: 43200B: 7200C: 60D: 120
参考答案: B 本题解释:B。
67、小鲸鱼说:“妈妈,我到您现在这么大时,您就31岁啦!”大鲸鱼说:“我像你这么大年龄时,你只有1岁。”请问小鲸鱼现在几岁?_____
A: 13B: 12C: 11D: 10
参考答案: C 本题解释: C【解析】由题意可得:设小鲸鱼有x岁,大鲸鱼为y岁,则可得出y+(y-x)=31,x-(y-x)=1,解得x=11。故选C。
68、用1元钱买4分、8分、1角的邮票共15张,那么最多可以买1角的邮票几张?_____
A: 6B: 7C: 8D: 9
参考答案: A 本题解释:参考答案:A题目详解:解法一:根据题意,可知:假设15张都买4分的,就多出钱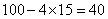 分。一张1角去代替一张4分,要多花6分钱,一张8分去替代一张4分,要多花4分钱;
分。一张1角去代替一张4分,要多花6分钱,一张8分去替代一张4分,要多花4分钱; ,因此15张4分中,有6张可用1角代替,1张用8分代替;即最多可以买1角邮票6张。因此,选A解法二:设可买4分x张,8分的y张,1角的z张,则:
,因此15张4分中,有6张可用1角代替,1张用8分代替;即最多可以买1角邮票6张。因此,选A解法二:设可买4分x张,8分的y张,1角的z张,则: 消元得:
消元得: 易见z最大为6。因此,选A(该解析由用户“dengdeng”于2011-04-0518:01:58贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之算式计算>不定方程问题>多元一次不定方程(组)
易见z最大为6。因此,选A(该解析由用户“dengdeng”于2011-04-0518:01:58贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之算式计算>不定方程问题>多元一次不定方程(组)
69、五个数写成一排,前三个数平均值是15,后两个数平均值是10,则这五个数的平均值是_____。
A: 11B: 12.5C: 13D: 14
参考答案: C 本题解释:正确答案是C考点平均数问题解析根据题干可知,前三个数的和为15×3=45,后两个数的和为10×2=20,则五个数的和为65,其平均数为13。故正确答案为C。
70、正六面体的表面积增加96%,棱长增加多少?_____
A: 20%B: 30%C: 40%D: 50%
参考答案: C 本题解释:【答案】C。解析:根据几何等比放缩性质,表面积为原来的1.96倍时,棱长为原来的1.4倍,因此棱长增加了40%。故正确答案为C。
71、一个停车场有50辆汽车,其中红色轿车35辆,夏利轿车28辆,有8辆既不是红色轿车又不是夏利轿车,停车场有红色夏利轿车多少辆?_____
A: 14B: 21C: 15D: 22
参考答案: B 本题解释:【解析】B。红色夏利=总数-红色非夏利-非红色非夏利-非红色夏利,红色非夏利=红色-红色夏利,非红色夏利=夏利-红色夏利,设则红色夏利=50-(35-红色夏利)-8-(28-红色夏利),得红色夏利=21。
72、(2007北京应届,第13题)某车间从3月2日开始每天调入一人,已知每人每天生产1件产品,该车间从3月1日至3月21日共生产840件产品,该车间原有工人多少名?_____
A: 20B: 30C: 35D: 40
参考答案: B 本题解释:参考答案:B题目详解:设车间原有工人n名,则人数应该是一个公差为1的等差数列。根据项数公式: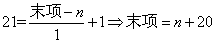 ,根据求和公式:
,根据求和公式: 考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
73、(2005上海,第10题)某单位共有36人。四种血型的人数分别是:A型12人,B型10人,AB型8人,O型6人。如果从这个单位随机地找出两个人,那么这两个人具有相同血型的概率为多少?_____
A: 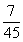 B:
B: 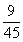 C:
C: 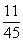 D:
D: 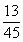
参考答案: C 本题解释:参考答案:C题目详解:从单位找出两个人有: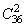 种方法;挑出两种A型血的人有:
种方法;挑出两种A型血的人有: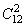 种方法;挑出两种AB型血的人有:
种方法;挑出两种AB型血的人有: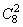 ;种方法;挑出两种O型血的人有:
;种方法;挑出两种O型血的人有: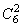 种方法;因此,两个人具有相同血型的概率为
种方法;因此,两个人具有相同血型的概率为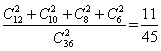 ;所以,选C。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选C。考查点:数量关系>数学运算>概率问题>条件概率
74、一个长方体的长、宽、高恰好是三个连续的自然数,并且它的体积数值等于它的所有棱长之和的2倍,那么这个长方体的表面积是_____
A: 74B: 148C: 150 D154
参考答案: B 本题解释: 【解析】B。设该长方体的长、宽、高分别是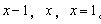 。那么有
。那么有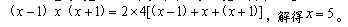 所以这个长方体的表面积为
所以这个长方体的表面积为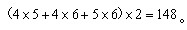
75、_____ 
A: AB: BC: CD: D
参考答案: A 本题解释:正确答案是A考点计算问题解析 秒杀技
秒杀技 标签韦达定理猜题技巧
标签韦达定理猜题技巧
76、(江苏2009A类-16)整数15具有被它的十位数字和个位数字同时整除的性质,则在12和50之间(包括12和50)具有这种性质的整数的个数是_____。
A: 8个B: 10个C: 12个D: 14个
参考答案: A 本题解释:参考答案:A本题得分:题目详解:根据题意,采用列举法:十位数字为1的数有12、15;十位数字为2的数有22、24;十位数字为3的数字有33、36;十位数字为4的数字有44、48.因此,这种性质的整数的个数是:2+2+2+2=8个;所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
77、某单位的员工不足50人,在参加全市组织的业务知识考试中全单位有1/7的人得90~100分,有1/2的人得80~89分,有1/3的人得60~79分,请问这个单位得60分(不包含60分)以下考试成绩的有多少人?_____
A: 1B: 2C: 3D: 4
参考答案: A 本题解释:参考答案:A题目详解:根据题意,该单位的人数必能被7,2,3整除,且不足50人;因此该单位的人数为:42人;得60分以下的人数: 。所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>三个数的最大公约数和最小公倍数
。所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>三个数的最大公约数和最小公倍数
78、甲乙两人相约见面,并约定第一人到达后,等15分钟不见第二人来就可以离去。假设他们都在10点至10点半的任一时间来到见面地点,则两人能见面的概率有多大?_____
A: 37.5%B: 50%C: 62.5%D: 75%
参考答案: D 本题解释:答案:D.[解析]本题为概率类题目。假设甲、乙分别在0-30分钟之内到达约会地点的情况如下图,则只有在阴影部分区域甲乙能够相遇,也就是求阴影部分面积的比例。很容易看出,阴影部分的面积为3/4=75%。
79、一个小于200的数,它除以11余8,除以13余10,那么这个数是多少?_____
A: 118B: 140C: 153D: 162
参考答案: B 本题解释:正确答案是B考点余数与同余问题解析解析1:可直接将4个选项带入,只有B符合题干要求。解析2:根据同余问题口诀”余同取余,和同加和,差同减差,公倍数做周期”,此处符合差同情形,也即除数与余数的差相同,而公倍数为11×13=143,因此被除数的表达式可写为143n-3,符合此表达式的仅B选项。标签直接代入
80、汽车往返甲、乙两地之间,上行速度为30公里/时,下行速度为60公里/时,汽车往返的平均速度为_____公里/时。
A: 40B: 45C: 50D: 55
参考答案: A 本题解释:正确答案是A考点工程问题解析解析1: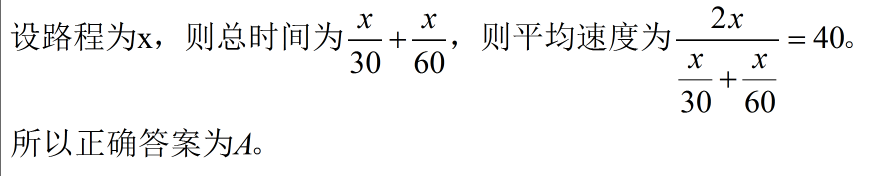 解析2:可直接根据等距离平均速度模型公式得到结果。平均速度=2×30×60/(30+60)=40,故正确答案为A。注:本方法是解析1的简化,不用设未知数,直接计算得到结果,建议使用。标签等距离平均速度模型
解析2:可直接根据等距离平均速度模型公式得到结果。平均速度=2×30×60/(30+60)=40,故正确答案为A。注:本方法是解析1的简化,不用设未知数,直接计算得到结果,建议使用。标签等距离平均速度模型
81、下图中的甲和乙都是正方形,BE=6厘米,EF=4厘米。那么,阴影部分ABC的面积是多少平方厘米?_____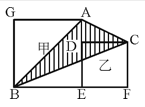
A: 20B: 24C: 21D: 18
参考答案: D 本题解释:正确答案是D考点几何问题解析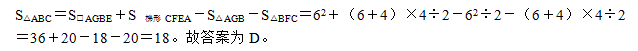
82、 _____
_____
A: 2cmB: 3cmC: 3.5cmD: 4cm
参考答案: A 本题解释:【答案】A。解析:
83、某公司面试员工,其中五分之二的应聘者获得了职位。最终录取者的平均分比录取线高7分,落选者的平均分比录取线低13分,所有应聘者的平均分为58分,则该公司的招聘录取分数线是多少?_____
A: 60B: 63C: 65D: 69
参考答案: B 本题解释:【答案】B。解析:设招聘的录取线是X,录取者的平均分为X+7,落选者的平均分为X-13,设共有5个应聘者,则录取者2个,所以,录取者总的得分2(X+7);落选者3个,落选者总的得分3(X-13)分;所有应聘者的得分为5分,所以,58×5=2(X+7)+3(X-13),可得X=63,可知答案为B。
84、一个球体的半径增加10%后,它的表面积增长百分之几?_____
A: l0%B: 21%C: 33.1%D: 22%
参考答案: B 本题解释:参考答案:B题目详解:根据题意,可知:球体的表面积计算公式为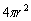 ,故半径增加10%后,表面积增加:
,故半径增加10%后,表面积增加: 。所以它的表面积增长了21%。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以它的表面积增长了21%。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
85、A,B两村庄分别在一条公路L的两侧,A到L的距离|AC|为1公里,B到L的距离|BD|为2公里,C,D两处相距6公里,欲在公路某处建一个垃圾站,使得A,B两个村庄到此处处理垃圾都比较方便,应建在离C处多少公里_____
A: 2.75B: 3.25C: 2D: 3
参考答案: C 本题解释:答案: C 解析:连接AB,交公路L于点E,E点就是A、B两个村庄到此处处理垃圾都比较方便的地方,三角形ACE相似于三角形BDE,则AC⊥CE=BD⊥DE,而CE+DE=6,AC=1,BD=2,解得CE=2,故应建在离C处2公里。
86、校对一份书稿,编辑甲每天的工作效率等于编辑乙、丙每天工作效率之和,丙的工作效率相当于甲、乙每天工作效率之和的1/5。如果三人一起校对只需6天就可完成。现在如果让乙一人单独校对这份书稿,则需要_____天才能完成。
A: 20B: 16C: 24D: 18
参考答案: D 本题解释:D 解析:三人一起完成校对需要6天,那么三人每天的效率之和是1/6。因为甲每天的工作效率等于乙、丙每天工作效率之和,那么甲的工作效率为1/12,乙、丙的效率和也是1/12。设乙单独完成校对需要x天,那么根据题意可得到方程:1/12-1/x=(1/12+1/x)×1/5解得x=18,即乙单独完成校对需要18天,正确答案为D。
87、某单位邀请10为教师中的6为参加一个会议,其中甲,乙两位不能同时参加,则邀请的不同方法有_____种。
A: 84B: 98C: 112D: 140
参考答案: D 本题解释: 答案【D】解析:按要求:甲、乙不能同时参加分成以下几类:A.甲参加,乙不参加,那么从剩下的8位教师中选出5位,有C(8,5)=56种;B.乙参加,甲不参加,同(a)有56种;C.甲、乙都不参加,那么从剩下的8位教师中选出6位,有C(8,6)=28种。故共有56+56+28=140种。
88、李大夫去山里给一位病人出诊,他下午1点离开诊所,先走了一段平路,然后爬上了半山腰,给那里的病人看病。半小时后,他沿原路下山回到诊所,下午3点半回到诊所。已知他在平路步行的速度是每小时4千米,上山每小时3千米,下山每小时6千米。请问:李大夫出诊共走了多少路?_____
A: 5千米B: 8千米C: 10千米D: l6千米
参考答案: B 本题解释: 
89、已知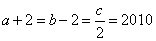 ,且
,且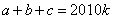 ,那么k的值为:_____
,那么k的值为:_____
A: 4B: 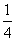 C: 一4D:
C: 一4D: 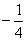
参考答案: A 本题解释:参考答案:A题目详解:由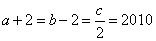 ,得:
,得: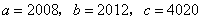 ;则:
;则: ,那么
,那么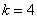 。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
90、如果a、b均为质数,且3a+7b=41,则a+b=_____
A: 5B: 6C: 7D: 8
参考答案: C 本题解释:C。a=2,b=5符合题意,选C。
91、小明今年a岁,芳芳明年(a-4)岁,再过c年,他们相差_____。
A: 4岁B: c+4岁C: 5岁D: c-3岁
参考答案: C 本题解释:【解析】不管过多少年,两人年龄差永远不会改变;今年芳芳是a-5岁,所以相差5岁,选C。
92、(2008浙江)小明、小刚和小红三人一起参加一次英语考试,已知考试共有100道题,且小明做对了68题,小刚做对了58题,小红做对了78题。问三人都做对的题目至少有几题?_____
A: 4题B: 8题C: 12题D: 16题
参考答案: A 本题解释:参考答案:A题目详解:本题可以解读为:做错的题目最多会有多少道。小明答错的为32题,小刚答错的为42题,小红答错的为22题,当他们三人答错的题目各不相同的时候,错题的数量最大。所以错题最多是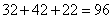 道,也就是至少有100-96=4道题目是三人全对的。因此,选A。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
道,也就是至少有100-96=4道题目是三人全对的。因此,选A。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
93、如图,已知直角梯形ABCD的上底长18厘米,下底长27厘米,高24厘米,三角形ABF、三角形ADE和四边形AECF’面积相等。三角形AEF的面积为多少平方厘米?_____ 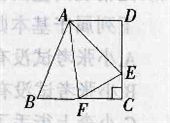
A: 165B: 132C: 160D: 156
参考答案: D 本题解释:参考答案 题目详解:依题意:
题目详解:依题意: 平方厘米;且
平方厘米;且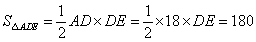 平方厘米;故
平方厘米;故 厘米;则
厘米;则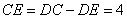 厘米;
厘米; 方厘米;故
方厘米;故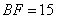 厘米,
厘米,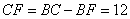 厘米,
厘米,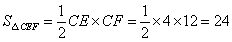 平方厘米;
平方厘米;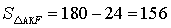 平方厘米;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
平方厘米;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
94、已知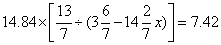 ,则
,则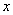 的值是_____
的值是_____
A: 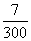 B:
B: 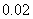 C:
C: 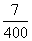 D:
D: 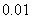
参考答案: D 本题解释:参考答案 题目详解:观察可知14.84是7.42的2倍,则原式整理为
题目详解:观察可知14.84是7.42的2倍,则原式整理为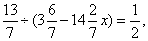 则
则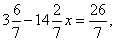 解得
解得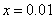 。所以,选D考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
。所以,选D考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
95、有一项工作任务,小明先做4小时,小方接着做8小时可以完成,小明先做6小时,小方接着做4小时也可以完成,如果小明先做2小时后再让小方接着做,那么小方可以完成工作还需要几个小时?_____
A: 8B: 10C: 11D: 12
参考答案: D 本题解释:正确答案是D考点工程问题解析解析1:小明先做4个小时,小方接着做8个小时可以完成,小明先做6个小时,小方接着做4个小时完成,即小明先增加2个小时工作,小方后面可以减小4个小时的工作(反之亦然),如果小明先只工作2个小时,即比第一种情况小明减少了2个小时工作,小方必须增加4个小时的工作,所以小明接着工作8+4=12(小时),故正确答案为D。解析2:设总的任务为为1,则小明的效率为x,小方的效率为y,则有4x+8y=1,6x+4y=1,解得x=1/8,y=1/16,则小明做2小时还剩1-2×(1/8)=3/4,小方还需要做3/4÷1/16=12(小时),故正确答案为D。
96、乘火车从甲城到乙城,1998年初需要19.5小时,1998年火车第一次提速30%,1999年第二次提速25%,2000年第三次提速20%。经过三次提速后,从甲城到乙城乘火车只需要_____。
A: 8.19小时B: 10小时C: 14.63小时D: 15小时
参考答案: B 本题解释:正确答案是B考点行程问题解析设1998年火车的速度为v,三次提速后所需时间为t,三次提速后速度为(1+30%)×(1+25%)×(1+20%)vt=19.5v,解得t=10。因此正确答案为B。
97、甲、乙、丙三个工程队的效率比为6:5:4,现将A、B两项工作量相同的工程交给这三个工程队,甲队负责A工程,乙队负责B工程,丙队参与A工程若干天后转而参与B工程。两项工程同时开工,耗时16天同时结束,问丙队在A工程中参与施工多少天?_____
A: 6B: 7C: 8D: 9
参考答案: A 本题解释:正确答案是A考点工程问题解析解析1:根据题目给出的效率比,直接赋值三个工程队的效率分别为6、5、4,并假设丙队参与A工程Y天,则根据题意可得6×16+4Y=5×16+4(16-Y),解得Y=6。故正确答案为A。解析2:根据题目中的效率比,直接赋值三个工程队的效率分别为6、5、4,将两工程合在一起看整体,则三个工程队一天的工作量为6+5+4=15,则16天的总工作量为15×16=240,于是A工程的工作量为120,其中甲完成了6×16=96,则丙需要参与(120-96)÷4=6天。故正确答案为A。秒杀技秒杀1:将效率比看做份数,甲比乙每天多1份,16天则多16份,而丙一天完成4来源:91考试网 91eXAm.org份,因此完成这16份需要4天,也即丙参与A工程比参与B工程少4天,于是参与A工程的天数为(16-4)÷2=6天。故正确答案为A。秒杀2:由题意甲效率高于乙效率,因此丙必然在甲中参与天数少于16天的一半,也即答案只在A、B中选择,这两个选项中,优先考虑代入A选项验证,符合条件,故正确答案为A。标签直接代入赋值思想
98、某城市9月平均气温为28.5度,如当月最热日和最冷日的平均气温相差不超过10度,则该月平均气温在30度及以上的日子最多有多少天?_____
A: 24B: 25C: 26D: 27
参考答案: B 本题解释:设该月的日平均气温在30度及以上的日子为2天,要使其最多,则最热日的气温应尽可能地接近30度,故可假设最热日的气温都是30度,最冷日的气温都是20度,根据题意可知,30x+20×(30一x)≤28.5×30→x≤25.5。故选B。
99、某天体沿正圆形轨道绕地球一圈所需时间为29.53059天,转速约1公里/秒。假设该天体离地球的距离比现在远10万公里而转速不变,那么该天体绕地球一圈约需要多少天?_____
A: 31 B: 32 C: 34 D: 37
参考答案: D 本题解释: D。算式为[29.53059×24×60×60×1/π+100000×2]×π÷1÷60÷60÷24≈36.8天,所以答案为D项。
100、甲、乙两名运动员在400米的环形跑道上练习跑步,甲出发1分钟后乙同向出发,乙出发2分钟后第一次追上甲,又过了8分钟,乙第二次追上甲,此时乙比甲多跑了250米,问两人出发地相隔多少米:_____
A: 200B: 150C: 100D: 50
参考答案: B 本题解释:正确答案是B,解析方法一:设甲与乙的速度分别为 和
和 ,由题意,从第一次乙追上甲到第二次追及,甲与乙的路程差为400米,故
,由题意,从第一次乙追上甲到第二次追及,甲与乙的路程差为400米,故 ,解得两人速度差为
,解得两人速度差为 ,由于甲一共跑了11分钟,乙一共跑了10分钟,在后10分钟内,乙比甲多跑了
,由于甲一共跑了11分钟,乙一共跑了10分钟,在后10分钟内,乙比甲多跑了 ,由于乙最终比甲多跑250米,故甲最开始的1分钟跑了250米,又根据乙2分钟时第一次追上甲,可得该过程中甲与乙的路程差为
,由于乙最终比甲多跑250米,故甲最开始的1分钟跑了250米,又根据乙2分钟时第一次追上甲,可得该过程中甲与乙的路程差为 ,故两人最初相距
,故两人最初相距 。方法二:直接分析,在两人第一次相遇到第二次相遇的过程中,乙比甲多跑了400米,故在最开始的两分钟内甲比乙多跑150米,故两人开始时相距150米。故正确答案为B。考点:行程问题
。方法二:直接分析,在两人第一次相遇到第二次相遇的过程中,乙比甲多跑了400米,故在最开始的两分钟内甲比乙多跑150米,故两人开始时相距150米。故正确答案为B。考点:行程问题