题34表            某厂商市场概率与收入矩阵表（单位：万元）

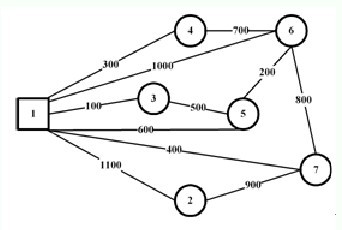
35．某住宅区安装供水管道如题35图。图中：方框表示供水管道的进水阀门，圆圈代表住宅，连线表示可以铺设的管道线路，线上数据表示距离（单位：米）。试以最小枝杈树方法画出最优管道线路方案，并计算管道的 总长度。

36．某公司现有位于不同城市的两个工厂A、B和3个仓库U、V、W。考虑公司的发展，公司决定选择在X城新建一个工厂，各工厂生产能力、仓库需求及工厂到仓库的单位运费如题36表。试建立供需平衡的运输表，并以西北角法求其最初的运输方案。

题36表      各工厂生产能力、仓库需求及工厂到仓库的单位运费表

六、计算题Ⅲ(本大题共2小题，每小题7分，共14分)

写出下列每小题的计算过程，否则只给结果分。

37．某公司产品生产需要A、B两种原料的总量至少为350吨，其中A原料至少购进125吨。加工每吨原料A需要2小时，加工每吨原料B需要1小时，而公司的加工能力总共只有600小时；每吨原料A价格为2万元，每吨原料B价格为3万元，试求在满足生产需要前提下，在公司加工能力范围内，如何购买两种原料可使总成本最低？试建立该问题的线性规划数学模型并用图解法求出最优解。

38．将37题线性规划问题转换为标准形式，以原点为基础求出基础可行解，并建立初始单纯形表。

七、计算题 Ⅳ(本大题共2小题，每小题8分，共16分)

写出下列每小题的计算过程，否则只给结果分。

39．某企业设备安装工程有10项活动，其各项活动的明细表如题39表。试绘制网络图。

题39表                    某企业安装工程活动明细表