C.ρ=0                                                             D.ρ=－1

8.已知随机变量X的概率密度为f _X(x)，令Y=2X，则Y的分布函数F_Y(y)是

9.设X₁，X₂，…，X_n，…是独立同分布的随机序列，且具有相同的数学期望和方差E(X_i)=0.1，D(X_i)=0.09(i=1，2，…，n，…)，则=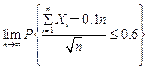

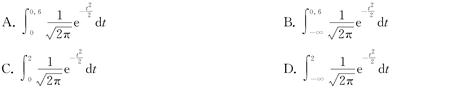
10.设随机变量X和Y相互独立且同服从正态分布N(0，4).从中分别抽取样本X₁，X₂和Y₁，Y₂，则统计量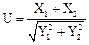服从

A.t(2)                                                              B.t(4)

C.χ²(2)                                                             D.χ²(4)

非选择题部分

注意事项：

　　用黑色字迹的签字笔或钢笔将答案写在答题纸上，不能答在试题卷上。

二、填空题(本大题共15小题，每小题2分，共30分)

11.设A，B分别表示甲、乙两人投篮命中，则A∪B表示的事件是______.

12.设随机变量X服从参数为1的泊松分布，则P{X=2}=______.

13.设随机变量(X，Y)服从平面矩形区域D={(x，y)|0≤x≤2，－1≤y≤1}的均匀分布，其联合概率密度函数是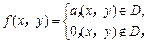则a=______.

14.设随机变量X服从正态分布N(55，100)，则P{X≥45}=______.(Φ(1)=0.8413)

15.设二维随机变量(X，Y)的分布律如下：

则b=______.

16.将不同的两封信随机地投入3个邮筒中，则第一个邮筒中有一封信的概率是______.

17.设随机变量X服从参数为0.5的指数分布，则E(X²)=______.

18.设随机变量X，Y相互独立且都服从卡方分布χ²(2)，则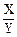服从______分布.(写出参数)

19.在假设检验中，显著性水平α就是犯______错误的概率.

20.已知随机变量X的分布函数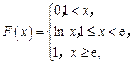则P{X≥2}=______.

21.已知P(A)=0.7，P(B)=0.4，P(A－B)=0.5，则P(A|B)=______.

22.已知二维随机变量(X，Y)的方差为：D(X)=16，D(Y)=25，若D(X+Y)=49，则Cov(X，Y)=______.

23.设随机变量X服从卡方分布χ²(n)，若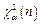是自由度为n的卡方分布的α分位数，则=______.

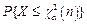24.设随机变量X服从二项分布B(2，0.1)，若随机变量Y=2X－1，则P{Y>0}=______.

25.设总体X服从二项分布B(10，p)，x₁，x₂，…，x_n是从总体X中抽取的一个简单随机样本，则参数p的矩估计是______.

三、计算题（本大题共2小题，每小题8分，共16分）

26.试卷中有一道选择题，共有4个答案可供选择，其中只有1个答案是正确的.任一考生如果会解这道题，则一定能选出正确答案；如果不会解这道题，则不妨任选1个答案.设考生会解这道题的概率是0.8.

(1)求考生选出正确答案的概率；

(2)已知某考生所选答案是正确的，求他确实会解这道题的概率.

27.现有6组观测数据，由下表给出：

试用最小二乘法建立y对x的线性回归方程.

四、综合题（本大题共2小题，每小题12分，共24分）

28.设随机变量X的分布律为

求：(1)随机变量X的分布函数F(x)；(2)E(X)，D(X).

29.设二维随机变量(X，Y)的概率密度函数是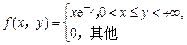

(1)求X和Y的边缘概率密度函数；

(2)问X与Y是否相互独立，为什么?

(3)求E(X)，E(Y).

五、应用题（本大题10分）

30.某种零件的椭圆度服从正态分布.改变工艺前抽取16件，测得数据并算得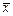=0.081，s_X=0.025；改变工艺后抽取20件，测得数据并计算得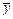=0.07，s_Y=0.02，问：改变工艺前后，方差有无明显差异?(显著性水平α取0.05)

(附：F_α/2(15，19)=2.6171，F_α/2(19，15)=2.7559)