|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
题目序号后的方框用2B铅笔涂黑.如果全选,则按第15题作答结果计分.)
 15.(选修4-1:几何证明选讲) 15.(选修4-1:几何证明选讲)
如图,PA是圆的切线,A为切点,PBC是圆的割线,
且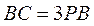 ,则 ,则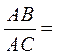 . .
16.(选修4-4:坐标系与参数方程)
在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系. 已知直线l的极坐标方程为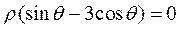 ,曲线C的参数方程为 ,曲线C的参数方程为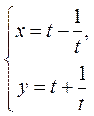 ( t为参数) ,l与C相交于A ( t为参数) ,l与C相交于A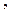 B两点,则 B两点,则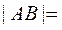 . .
三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分11分)
某同学用“五点法”画函数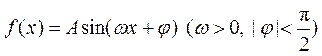 在某一个周期内的图象 在某一个周期内的图象
时,列表并填入了部分数据,如下表:
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数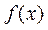 的解 的解
析式;
(Ⅱ)将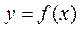 图象上所有点向左平行移动 图象上所有点向左平行移动 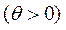 个单位长度,得到 个单位长度,得到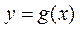 的图 的图
象. 若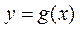 图象的一个对称中心为 图象的一个对称中心为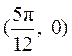 ,求 ,求 的最小值. 的最小值.
18.(本小题满分12分)
设等差数列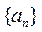 的公差为d,前n项和为 的公差为d,前n项和为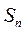 ,等比数列 ,等比数列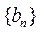 的公比为q.已知 的公比为q.已知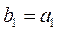 , ,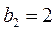 , ,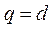 , ,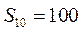 . .
(Ⅰ)求数列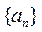 , ,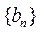 的通项公式; 的通项公式;
(Ⅱ)当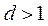 时,记 时,记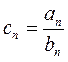 ,求数列 ,求数列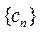 的前n项和 的前n项和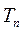 . .
19.(本小题满分12分)
 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马 中,侧棱 中,侧棱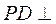 底面 底面 , ,
且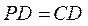 ,过棱 ,过棱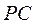 的中点 的中点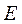 ,作 ,作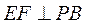 交 交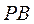 于 于
点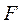 ,连接 ,连接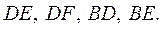
(Ⅰ)证明: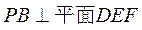 .试判断四面体 .试判断四面体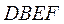 是 是
否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
(Ⅱ)若面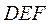 与面 与面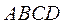 所成二面角的大小为 所成二面角的大小为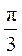 , ,
求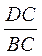 的值. 的值.
20.(本小题满分12分)
某厂用鲜牛奶在某台设备上生产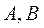 两种奶制品.生产1吨 两种奶制品.生产1吨 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨 产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天 产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天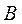 产品的产量不超过 产品的产量不超过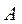 产品产量的2倍,设备每天生产 产品产量的2倍,设备每天生产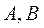 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利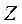 (单位:元)是一个随机变量. (单位:元)是一个随机变量.
(Ⅰ)求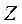 的分布列和均值; 的分布列和均值;
(Ⅱ) 若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
21.(本小题满分14分)
一种作图工具如图1所示.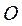 是滑槽 是滑槽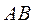 的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且 的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且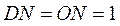 , ,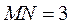 .当栓子D在滑槽AB内作往复运动时,带动N绕 .当栓子D在滑槽AB内作往复运动时,带动N绕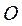 转动一周(D不动时,N也不动),M处的笔尖画出的曲线记为C.以 转动一周(D不动时,N也不动),M处的笔尖画出的曲线记为C.以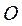 为原点, 为原点,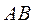 所在的直线为 所在的直线为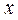 轴建立如图2所示的平面直角坐标系. 轴建立如图2所示的平面直角坐标系.
(Ⅰ)求曲线C的方程;
(Ⅱ)设动直线 与两定直线 与两定直线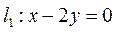 和 和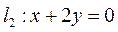 分别交于 分别交于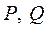 两点.若直线 两点.若直线
总与曲线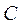 有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若 有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若
存在,求出该最小值;若不存在,说明理由.
22.(本小题满分14分)
已知数列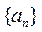 的各项均为正数, 的各项均为正数,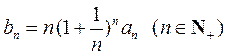 ,e为自然对数的底数. ,e为自然对数的底数.
(Ⅰ)求函数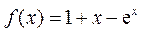 的单调区间,并比较 的单调区间,并比较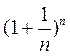 与e的大小; 与e的大小;
(Ⅱ)计算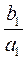 , ,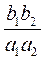 , ,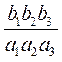 ,由此推测计算 ,由此推测计算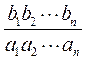 的公式,并给出证明; 的公式,并给出证明;
(Ⅲ)令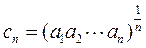 ,数列 ,数列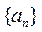 , ,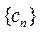 的前 的前 项和分别记为 项和分别记为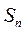 , ,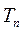 , 证明: , 证明: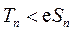 . .
绝密★启用前
2015年普通高等学校招生全国统一考试(湖北卷)
数学(理工类)试题参考答案
一、选择题(本大题共10小题,每小题5分,共50分)
1.A 2.B 3.D 4.C 5.A 6.B 7.B 8.D 9.C 10.B
二、填空题(本大题共6小题,考生需作答5小题,每小题5分,共25分)
11.9 12.2 13.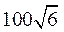
14.(Ⅰ)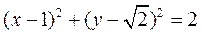 ;(Ⅱ)①②③ 15. ;(Ⅱ)①②③ 15.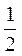 16. 16.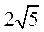
三、解答题(本大题共6小题,共75分)
17.(11分)
(Ⅰ)根据表中已知数据,解得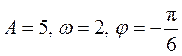 . 数据补全如下表: . 数据补全如下表:
且函数表达式为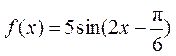 . .
(Ⅱ)由(Ⅰ)知 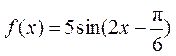 ,得 ,得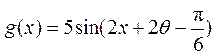 . .
因为 的对称中心为 的对称中心为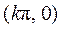 , ,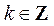 . .
令 ,解得 ,解得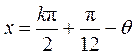 , ,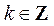 . .
由于函数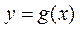 的图象关于点 的图象关于点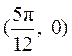 成中心对称,令 成中心对称,令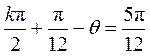 , ,
解得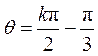 , ,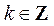 . 由 . 由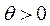 可知,当 可知,当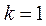 时, 时, 取得最小值 取得最小值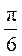 . .
18.(12分)
(Ⅰ)由题意有,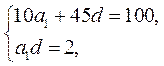 即 即
解得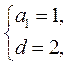 或 或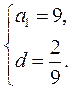 故 故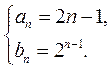 或 或
(Ⅱ)由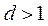 ,知 ,知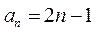 , ,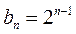 ,故 ,故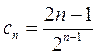 ,于是 ,于是
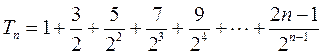 , ① , ①
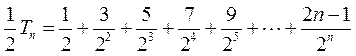 . ② . ②
①-②可得
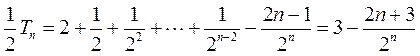 , ,
故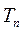  . .
19.(12分)
(解法1)
(Ⅰ)因为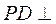 底面 底面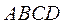 ,所以 ,所以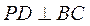 , ,
由底面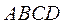 为长方形,有 为长方形,有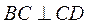 ,而 ,而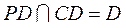 , ,
所以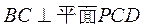 . 而 . 而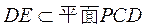 ,所以 ,所以 . .
又因为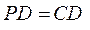 ,点 ,点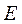 是 是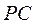 的中点,所以 的中点,所以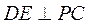 . .
而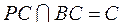 ,所以 ,所以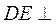 平面 平面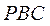 . 而 . 而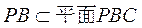 ,所以 ,所以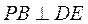 . .
又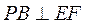 , ,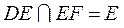 ,所以 ,所以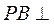 平面 平面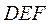 . .
由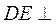 平面 平面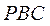 , ,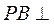 平面 平面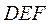 ,可知四面体 ,可知四面体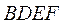 的四个面都是直角三角形, 的四个面都是直角三角形,
即四面体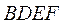 是一个鳖臑,其四个面的直角分别为 是一个鳖臑,其四个面的直角分别为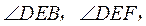 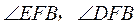 . .
(Ⅱ)如图1,在面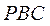 内,延长 内,延长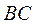 与 与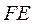 交于点 交于点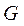 ,则 ,则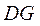 是平面 是平面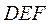 与平面 与平面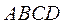
的交线. 由(Ⅰ)知,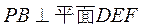 ,所以 ,所以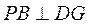 . .
又因为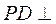 底面 底面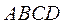 ,所以 ,所以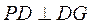 . 而 . 而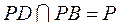 ,所以 ,所以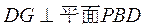 . .
故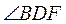 是面 是面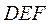 与面 与面 所成二面角的平面角, 所成二面角的平面角,
设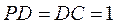 , ,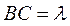 ,有 ,有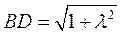 , ,
在Rt△PDB中, 由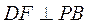 , 得 , 得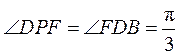 , ,
则 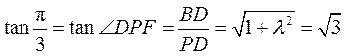 , 解得 , 解得 . .
所以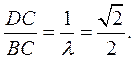
故当面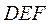 与面 与面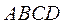 所成二面角的大小为 所成二面角的大小为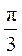 时, 时,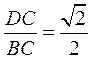 . .
(解法2)
(Ⅰ)如图2,以 为原点,射线 为原点,射线 分别为 分别为 轴的正半轴,建立空间直角坐标系. 设 轴的正半轴,建立空间直角坐标系. 设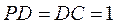 , ,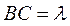 ,则 ,则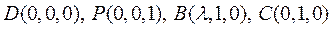 , ,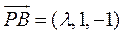 ,点 ,点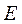 是 是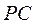 的中点,所以 的中点,所以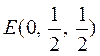 , ,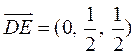 , ,
于是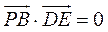 ,即 ,即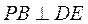 . .
又已知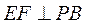 ,而 ,而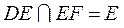 ,所以 ,所以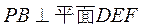 . .
因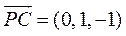 , , 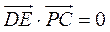 , 则 , 则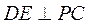 , 所以 , 所以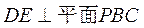 . .
由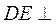 平面 平面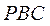 , ,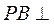 平面 平面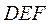 ,可知四面体 ,可知四面体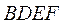 的四个面都是直角三角形, 的四个面都是直角三角形,
 即四面体 即四面体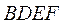 是一个鳖臑,其四个面的直角分别为 是一个鳖臑,其四个面的直角分别为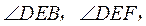 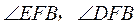 . .
(Ⅱ)由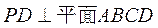 ,所以 ,所以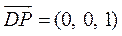 是平面 是平面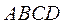 的一个法向量; 的一个法向量;
由(Ⅰ)知,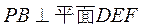 ,所以 ,所以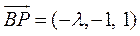 是平面 是平面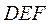 的一个法向量. 的一个法向量.
若面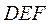 与面 与面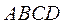 所成二面角的大小为 所成二面角的大小为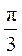 , ,
则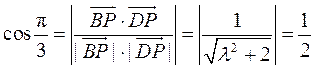 , ,
解得 . 所以 . 所以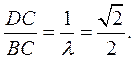
故当面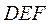 与面 与面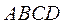 所成二面角的大小为 所成二面角的大小为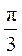 时, 时,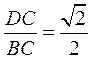 . .
20.(12分)
(Ⅰ)设每天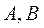 两种产品的生产数量分别为 两种产品的生产数量分别为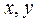 ,相应的获利为 ,相应的获利为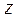 ,则有 ,则有
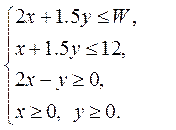 (1) (1)
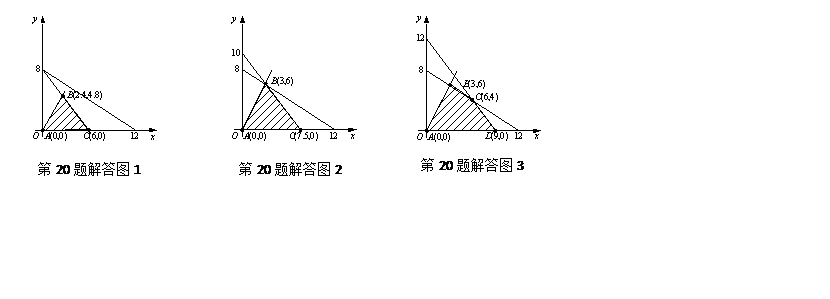 目标函数为 目标函数为 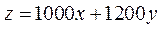 . &n . &n
|