|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
bsp;
当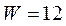 时,(1)表示的平面区域如图1,三个顶点分别为 时,(1)表示的平面区域如图1,三个顶点分别为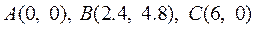 . .
将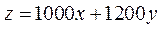 变形为 变形为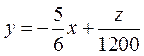 , ,
当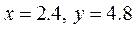 时,直线 时,直线 : :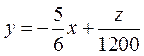 在 在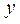 轴上的截距最大, 轴上的截距最大,
最大获利 . .
当 时,(1)表示的平面区域如图2,三个顶点分别为 时,(1)表示的平面区域如图2,三个顶点分别为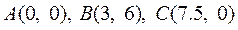 . .
将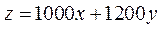 变形为 变形为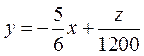 , ,
当 时,直线 时,直线 : :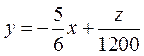 在 在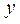 轴上的截距最大, 轴上的截距最大,
最大获利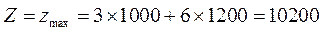 . .
当 时,(1)表示的平面区域如图3, 时,(1)表示的平面区域如图3,
四个顶点分别为 . .
将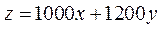 变形为 变形为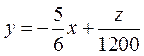 , ,
当 时,直线 时,直线 : :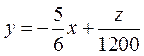 在 在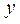 轴上的截距最大, 轴上的截距最大,
最大获利 . .
故最大获利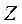 的分布列为 的分布列为
|
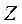
|
8160 |
10200 |
10800 |
|
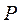
|
0.3 |
0.5 |
0.2 |
因此,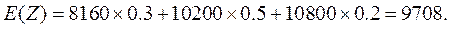
(Ⅱ)由(Ⅰ)知,一天最大获利超过10000元的概率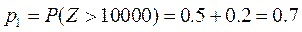 , ,
由二项分布,3天中至少有1天最大获利超过10000元的概率为

21.(14分)
(Ⅰ)设点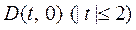 , , ,依题意, ,依题意,
 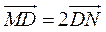 ,且 ,且 , ,
所以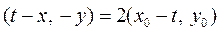 ,且 ,且
即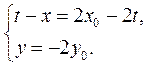 且 且
由于当点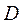 不动时,点 不动时,点 也不动,所以 也不动,所以 不恒等于0, 不恒等于0,
于是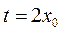 ,故 ,故 ,代入 ,代入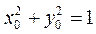 ,可得 ,可得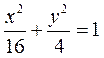 , ,
即所求的曲线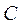 的方程为 的方程为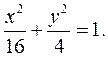
(Ⅱ)(1)当直线 的斜率不存在时,直线 的斜率不存在时,直线 为 为 或 或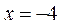 ,都有 ,都有 . .
(2)当直线 的斜率存在时,设直线 的斜率存在时,设直线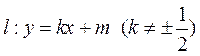 , ,
由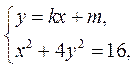 消去 消去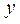 ,可得 ,可得 . .
因为直线 总与椭圆 总与椭圆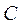 有且只有一个公共点, 有且只有一个公共点,
所以 ,即 ,即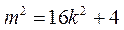 . ① . ①
又由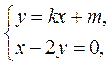 可得 可得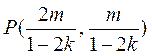 ;同理可得 ;同理可得 . .
由原点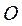 到直线 到直线 的距离为 的距离为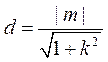 和 和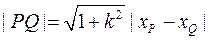 ,可得 ,可得
 . ② . ②
将①代入②得,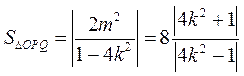 . .
当 时, 时, ; ;
当 时, 时, . .
因 ,则 ,则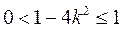 , , ,所以 ,所以 , ,
当且仅当 时取等号. 时取等号.
所以当 时, 时,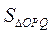 的最小值为8. 的最小值为8.
综合(1)(2)可知,当直线 与椭圆 与椭圆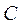 在四个顶点处相切时,△OPQ的面积取得最小值8. 在四个顶点处相切时,△OPQ的面积取得最小值8.
22.(14分)
(Ⅰ)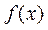 的定义域为 的定义域为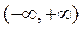 , ,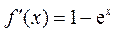 . .
当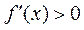 ,即 ,即 时, 时,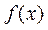 单调递增; 单调递增;
当 ,即 ,即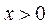 时, 时,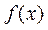 单调递减. 单调递减.
故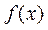 的单调递增区间为 的单调递增区间为 ,单调递减区间为 ,单调递减区间为 . .
当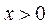 时, 时, ,即 ,即 . .
令 ,得 ,得 ,即 ,即 . ① . ①
(Ⅱ) ; ; ; ;
 . .
由此推测: 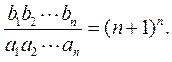 ② ②
下面用数学归纳法证明②.
(1)当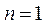 时,左边 时,左边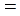 右边 右边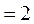 ,②成立. ,②成立.
(2)假设当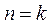 时,②成立,即 时,②成立,即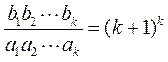 . .
当 时, 时, ,由归纳假设可得 ,由归纳假设可得
 . .
所以当 时,②也成立. 时,②也成立.
根据(1)(2),可知②对一切正整数n都成立.
(Ⅲ)由 的定义,②,算术-几何平均不等式, 的定义,②,算术-几何平均不等式, 的定义及①得 的定义及①得
 
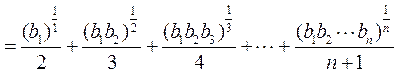
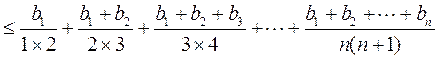

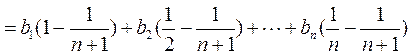
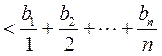 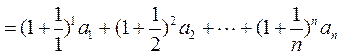
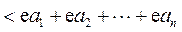 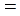 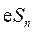 . .
即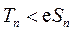 . .
|