1、选择题  如图所示，在固定的光滑水平杆(杆足够长)上，套有一个质量为m="0.5" kg的光滑金属圆环，轻绳一端拴在环上，另一端系着一个质量为M=1.98kg的木块，现有一质量为m0=20g的子弹以v0=100m/s的水平速度射入木块并留在木块中(不计空气阻力和子弹与木块作用的时间，g取10m/s2)，求：

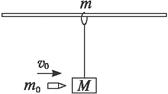
①圆环、木块和子弹这个系统损失的机械能；
②木块所能达到的最大高度．

参考答案：（1）99J（2）0.01m

本题解析：①子弹射入木块过程，动量守恒，则有
?
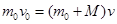v=1m/s?
机械能只在该过程有损失，损失的机械能为
?
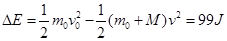②木块（含子弹）在向上摆动过程中，木块（含子弹）和圆环水平方向动量守恒，则有：
?
?
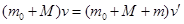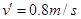根据机械能守恒定律有?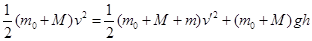
联立解得h=0.01m

本题难度：一般

2、选择题  质量为m的物体，以速度v离开高为H的桌子,当它落到距地面高为h的A点时速度为vA，在不计空气阻力的情况下,以地面为参考面，下列说法不正确的是

A．物体在A点具有的重力势能为mgh
B．物体在A点具有的机械能是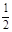mV+mgh
C．物体在A点具有的动能是mg(H－h)
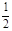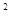D．物体落地瞬间具有的机械能是m V+mgh

参考答案：D

本题解析：运动过程中，小球只受重力作用，机械能是守恒的，所以若取地面为零势能面，物体在A点具有的机械能为。若取桌面为零势能面，物体在A点具有的机械能是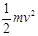，AB正确，重力势能的减小量转化为动能了所以物体在A点具有的动能是，C正确。D错误。

本题难度：简单

3、计算题  如图所示，有一轻质杆OA，可绕O点在竖直面内自由转动，在杆的另一端A点和中点B各固定一个质量都为m的小球，设杆长为L，开始时，杆静止在水平位置，求释放杆后，杆转到竖直位置时，B球的速度是多少？

参考答案：

本题解析：

本题难度：困难

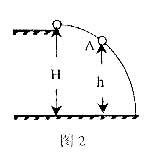
4、选择题  如图所示，M为固定在水平桌面上的有缺口的方形木块，abcd为半径是R的光滑圆弧形轨道，a为轨道的最高点，de面水平且有一定长度．今将质量为m的小球在d点的正上方高为h处由静止释放，让其自由下落到d处切入轨道内运动，不计空气阻力，则

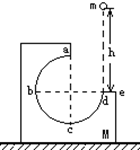
A．只要h大于R，释放后小球就能通过a点
B．只要改变h的大小，就能使小球通过a点后，既可能落回轨道内，又可能落到de面上
C．无论怎样改变h的大小，都不可能使小球通过a点后落回轨道内
D．无论怎样调节h的大小，都不可以使小球飞出de面之外(即e的右侧)

参考答案：C

本题解析：据题意，当小球从h高处自由释放，只有小球的速度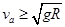小球才可以通过a点，据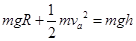可得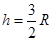，即只有使小球的高度h大于或等于这个高度才可以通过a点，A选项错误；小球从a点飞出后做平抛运动，据求出平抛运动的时间为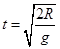，进而可以求出平抛运动的水平位移为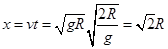，即一旦小球通过了a点，小球将不会再落回轨道内，B选项错误而C选项正确；据以上分析，只要h足够大，就可以使小球的水平位移大于de，所以D选项错误。

本题难度：一般

5、简答题  过山车质量均匀分布，从高为h的平台上无动力冲下倾斜轨道并进入水平轨道，然后进入竖直圆形轨道，如图17，已知过山车的质量为M，长为L，每节车厢长为a，竖直圆形轨道半径为R,L> 2πR，且R>>a，可以认为在圆形轨道最高点的车厢受到前后车厢的拉力沿水平方向，为了不出现脱轨的危险，h至少为多少？（用R、L表示，认为运动时各节车厢速度大小相等，且忽略一切摩擦力及空气阻力）

参考答案：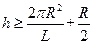

本题解析：取过山车为研究对象，过山车从平台上滑下到车厢占满竖直圆形轨道过程中，由于只有重力做功，故机械能守恒，竖直圆形轨道上的过山车可以把这部分的重心看作在轨道的圆心上，所以有：

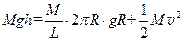?①（4 分）
在竖直方向受到重力和轨道对它向下的压力，受力分析如图所示，设一节车厢质量为m，则有：
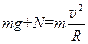? ② （3 分）N≥0 ?③ （3 分）
联立解得　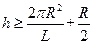? (4分)

本题难度：一般