1、计算题  气球质量为200kg，载有质量为50kg的人，静止在空中距地面20m高的地方，气球下悬一根质量可忽略不计的绳子，此人想从气球上沿绳慢慢下滑至地面，为了安全到达地面，则这根绳长至少应为多少米？（不计人的高度）

参考答案：解：以人和气球为研究对象（系统），这个系统所受重力与空气浮力平衡，故系统动量守恒，此系统类似于人船模型。设人的质量为，气球的质量为M，气球静止时离地高为H，当人到达地面时，气球又上升了h，则有：
其中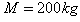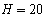，，m，即可求得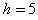：m
故此人要想从气球上沿绳慢慢安全到达地面，这根绳长至少应为：H+h=25 m

本题解析：

本题难度：一般

2、简答题  如图5-8所示，质量分别为mA="0.5" kg、mB="0.4" kg 的长板紧挨在一起静止在光滑的水平面上，质量为mC="0.1" kg的木块C以速度vC0="10" m/s滑上A板左端，最后C木块和B板相对静止时的共同速度vCB="1.5" m/s.求：

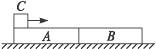
图5-8
（1）A板最后的速度vA；
（2）C木块刚离开A板时的速度vC.

参考答案：(1)0.5 m/s? (2)5.5 m/s

本题解析：C在A上滑动的过程中，A、B、C组成的系统动量守恒，则
mCvC0=mCvC+(mA+mB)vA
C在B上滑动时，B、C组成的系统动量守恒，则
mCvC+mBvA=(mC+mB)vCB
解得vA="0.5" m/s，vC="5.5" m/s.

本题难度：简单

3、计算题  如图所示，水平地面上有一上表面光滑的长木板C(其左端有一竖直小挡板)，其上放有可视为质点的两小物块A和B，其间夹有一根长度可忽略的轻弹簧，弹簧与物块间不相连，其中小物块B距离木板C的右端很近。已知mA=mB="4.0kg," mC=1.0kg地面与木板C间的动摩擦因数为μ=0.20，重力加速度为g=10m/s2。开始时整个装置保持静止，两个小物块A、B将轻质弹簧压紧使弹簧贮存了弹性势能E0=100J。某时刻同时释放A、B，则：
(1)当小物块B滑离木板最右端时，求两小物块的速度魄vA、vB；
(2)若小物块A与挡板的碰撞时间极短且无机械能损失，求在它们第一次碰撞的过程中小物块A对挡板的冲量大小；
(3)在小物块A与挡板第一次碰撞到第二次碰撞的过程中，求木板C的位移大小。

参考答案：

本题解析：略

本题难度：一般

4、计算题  如图所示，质量，长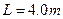的木板B静止在光滑水平地面上，其上表面正中央放置一个质量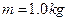的小滑块A，A与B之间的动摩擦因数为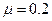。现同时给A、B瞬时冲量使二者获得水平向右的初速度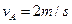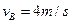，、；已知在B与墙壁碰撞前A没有滑离B，且A、B已经达到共同速度。设B与墙壁碰撞时间极短，且无机械能损失，重力加速度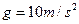。求：

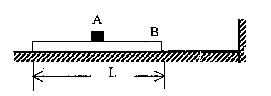
（1）B与墙壁碰撞前，A、B的共同速度大小；
（2）在B与墙壁碰撞前的过程中，A相对于B滑行的距离；
（3）A在B上滑动的整个过程中，A、B系统因摩擦产生的热量。

参考答案：(1)有题可知，B与墙碰撞前A、B已达共同速度V，对A、B系?统有动量守恒定律?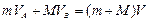?----3分?得 V="3.6m/s?" --------2分
（2）由功能关系?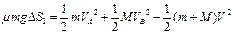?---3分
得? A相对于B向左滑行?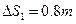?- ----2分
（3 ）B与墙碰撞后，设A、B达到共同速度V/时，A仍在B上，
对A、B系统有动量守恒定律?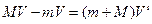?----2分
由功能关系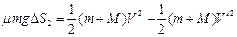? -----2分
得? A相对于B向右滑行??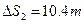
因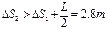? ----1分?所以在达共同速度前，A已从B右端滑出
故A、B系统因摩擦产生的热量为?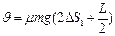----2分??----1分

本题解析：略

本题难度：简单

5、计算题  如图所示，质量为M的小车静止在光滑的水平面上，小车的最右端站着质量为m的人。若人水平向右以相对车的速度u跳离小车，则人脱离小车后小车的速度多大？方向如何？

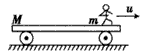
参考答案：解：设速度u的方向为正方向，并设人脱离车后小车的速度大小为v，则人对地的速度大小为（u -v）
根据动量守恒定律得0=m(u-v)-Mv
所以小车速度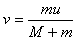，方向和u的方向相反

本题解析：

本题难度：一般