微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
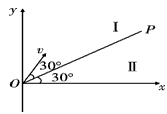
1、计算题 如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为 ,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是他们的边界,OP上方区域I中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成
,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是他们的边界,OP上方区域I中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成 角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:
角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:
(1)区域II中磁场的磁感应强度大小;
(2)Q点的坐标。
参考答案:解:(1)设质子在磁场I和II中做圆周运动的轨道半径分别为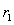 和
和 ,区域II中磁感应强度为
,区域II中磁感应强度为 ,由牛顿第二定律
,由牛顿第二定律
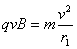 ?①?
?①?
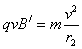 ?②
?②
粒子在两区域运动的轨迹如图所示: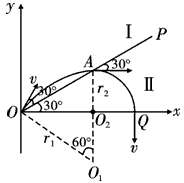 由几何关系可知,质子从A点出磁场I时的速度方向与OP的夹角为30°,故质子在磁场I中轨迹的圆心角为
由几何关系可知,质子从A点出磁场I时的速度方向与OP的夹角为30°,故质子在磁场I中轨迹的圆心角为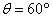
则 为等边三角形
为等边三角形
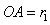 ?③
?③
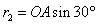 ?④
?④
由①②③④解得区域II中磁感应强度为
(2)Q点坐标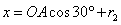
故x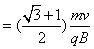
本题解析:
本题难度:困难
2、选择题 质子(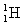 )和α粒子(
)和α粒子(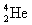 )以相同的速度垂直进入同一匀强磁场中,它们在垂直于磁场的平面内做匀速圆周运动,它们的轨道半径和运动周期关系是
)以相同的速度垂直进入同一匀强磁场中,它们在垂直于磁场的平面内做匀速圆周运动,它们的轨道半径和运动周期关系是
[? ]
A. RH:Rα=1:2,TH:Tα=1:2
B. RH:Rα=2:1,TH:Tα=1:2
C. RH:Rα=1:2,TH:Tα=2:1
D. RH:Rα=1:4,TH:Tα=1:4
参考答案:A
本题解析:
本题难度:一般
3、简答题 如图,ABCD是边长为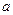 的正方形。质量为
的正方形。质量为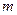 、电荷量为
、电荷量为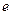 的电子以大小为
的电子以大小为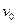 的初速度沿纸面垂直于BC边射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射,都只能从A点射出磁场。不计重力,求:
的初速度沿纸面垂直于BC边射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射,都只能从A点射出磁场。不计重力,求:

(1)次匀强磁场区域中磁感应强度的方向和大小;
(2)此匀强磁场区域的最小面积。
参考答案:见解析
本题解析:(1)设匀强磁场的磁感应强度的大小为B。令圆弧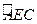 是自C点垂直于BC入射的电子在磁场中的运行轨道。电子所受到的磁场的作用力
是自C点垂直于BC入射的电子在磁场中的运行轨道。电子所受到的磁场的作用力


应指向圆弧的圆心,因而磁场的方向应垂直于纸面向外。圆弧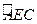 的圆心在CB边或其延长线上。依题意,圆心在A、C连线的中垂线上,故B 点即为圆心,圆半径为
的圆心在CB边或其延长线上。依题意,圆心在A、C连线的中垂线上,故B 点即为圆心,圆半径为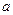 按照牛顿定律有
按照牛顿定律有

联立①②式得

(2)由(1)中决定的磁感应强度的方向和大小,可知自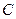 点垂直于
点垂直于 入射电子在A点沿DA方向射出,且自BC边上其它点垂直于入射的电子的运动轨道只能在BAEC区域中。因而,圆弧
入射电子在A点沿DA方向射出,且自BC边上其它点垂直于入射的电子的运动轨道只能在BAEC区域中。因而,圆弧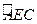 是所求的最小磁场区域的一个边界。
是所求的最小磁场区域的一个边界。
为了决定该磁场区域的另一边界,我们来考察射中A点的电子的速度方向与BA的延长线交角为 (不妨设
(不妨设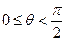 )的情形。该电子的运动轨迹
)的情形。该电子的运动轨迹 如右图所示。
如右图所示。
图中,圆 的圆心为O,pq垂直于BC边,由③式知,圆弧
的圆心为O,pq垂直于BC边,由③式知,圆弧 的半径仍为
的半径仍为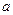 ,在D为原点、DC为x轴,AD为
,在D为原点、DC为x轴,AD为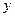 轴的坐标系中,P点的坐标
轴的坐标系中,P点的坐标 为
为

这意味着,在范围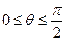 内,p点形成以D为圆心、
内,p点形成以D为圆心、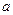 为半径的四分之一圆周
为半径的四分之一圆周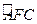 ,它是电子做直线运动和圆周运动的分界线,构成所求磁场区域的另一边界。
,它是电子做直线运动和圆周运动的分界线,构成所求磁场区域的另一边界。
因此,所求的最小匀强磁场区域时分别以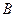 和
和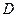 为圆心、
为圆心、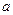 为半径的两个四分之一圆周
为半径的两个四分之一圆周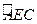 和
和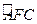 所围成的,其面积为
所围成的,其面积为
本题难度:一般
4、选择题 如图甲所示,一不计重力而质量为m、带电荷量为+q的粒子,在a点以某一个初速度水平射入一个磁场区域,沿曲线abcd运动,ab、bc、cd都是半径为R的圆弧。粒子在每段圆弧上运动的时间都为t。如果选由纸面垂直穿出的磁感应强度为正,则磁场区域I、Ⅱ、Ⅲ三部分的磁感应强度B随x变化的关系是图乙中的

[? ]
A、
B、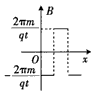
C、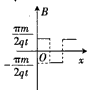
D、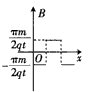
参考答案:C
本题解析:
本题难度:一般
5、选择题 如右图所示,带有正电荷的A粒子和B粒子同时以同样大小的速度从宽度为d的有界匀强磁场的边界上的O点分别以30°和60°(与边界的夹角)射入磁场,又恰好都不从另一边界飞出,则下列说法中正确的是
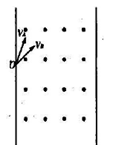
A.A、B两粒子在磁场中做圆周运动的半径之比是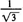
B.A、B两粒子在磁场中做圆周运动的半径之比是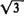
C.A、B两粒子的 之比是
之比是
D.A、B两粒子的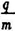 之比是
之比是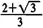
参考答案:D
本题解析:有几何关系的 ,所以两粒子在磁场中做圆周运动的半径之比
,所以两粒子在磁场中做圆周运动的半径之比 ,由
,由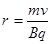 ,可得q/m之比与半径之比成反比,所以选D。
,可得q/m之比与半径之比成反比,所以选D。
本题难度:一般