微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 (9分)如图所示,足够长、宽度L1=0.1m、方向向左的有界匀强电场场强E=70 V/m,电场左边是足够长、宽度L2=0.2 m、磁感应强度B=2×10-3 T的有界匀强磁场。一带电粒子电荷量q=+3.2×10-19C,质量m=6.4×10-27 kg,以v=4×104 m/s的速度沿OO′垂直射入磁场,在磁场中偏转后进入右侧的电场,最后从电场右边界射出。(粒子重力不计)求:
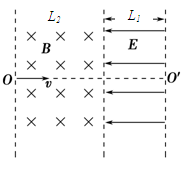
(1)带电粒子在磁场中运动的轨道半径和时间;
(2)带电粒子飞出电场时的速度大小。
参考答案:(1)0.4m; ;(2)3×104 m/s
;(2)3×104 m/s
本题解析:(1)带电粒子在磁场中运动时,由牛顿运动定律,有
qvB=m
R=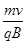 =
= m=0.4 m.
m=0.4 m.
轨迹如图所示,由L2=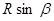 得β=π/6
得β=π/6
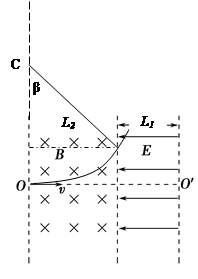
又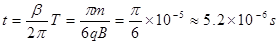
(2)由动能定理得: mv末2—
mv末2— mv2=—EqL1可得v末=3×104 m/s
mv2=—EqL1可得v末=3×104 m/s
考点:带电粒子在匀强电场及在匀强磁场中的运动;牛顿定律及动能定理.
本题难度:困难
2、选择题 三个速度大小不同的同种带电粒子,沿同一方向从图中长方形区域的匀强磁场上边缘射入当它们从下边缘飞出时对入射方向的偏角分别为90°、60°、30°,则它们在磁场中运动的时间之比为:

[? ]
A.1:1:1?
B.1:2:3?
C.3:2:1?
D.1: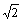 :
: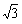
参考答案:C
本题解析:
本题难度:一般
3、计算题 (12分)下图是某装置的垂直截面图,虚线A1A2是垂直截面与磁场区边界面的交线,匀强磁场分布在A1A2的右侧区域,磁感应强度B=0.4T,方向垂直纸面向外,A1A2与垂直截面上的水平线夹角为45°。A1A2的左侧,固定的薄板和等大的挡板均水平放置,它们与垂直截面交线分别为S1、S2,相距L=0.2m。在薄板上P处开一小孔,P与A1A2线上点D的水平距离为L。在小孔处装一个电子快门。起初快门开启,一旦有带正电微粒通过小孔,快门立即关闭,此后每隔T=3.0×10-3s开启一次并瞬间关闭。从S1S2之间的某一位置水平发射一速度为v0的带正电微粒,它经过磁场区域后入射到P处小孔。通过小孔的微粒与档板发生碰撞而反弹,反弹速度大小是碰前的0.5倍。(忽略微粒所受重力影响,碰撞过程无电荷转移。已知微粒的荷质比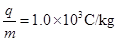 。只考虑纸面上带电微粒的运动)求:
。只考虑纸面上带电微粒的运动)求:
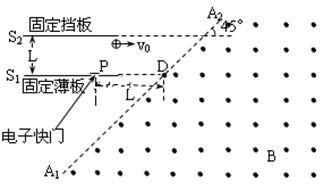
(1)满足题目的微粒在磁场中运动的半径的条件?
(2)经过一次反弹直接从小孔射出的微粒,其初速度v0应为多少?
(3)上述(2)问中微粒从最初水平射入磁场到第二次离开磁场的时间。
参考答案:(1)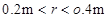 ;(2)v0="100m/s" ;(3)
;(2)v0="100m/s" ;(3)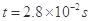
本题解析:(1)如图所示:
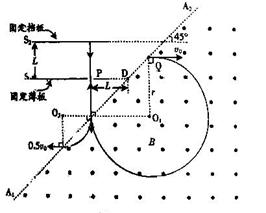
设带正电微粒在S1S2之间任意点Q以水平速度v0进入磁场,微粒受到的洛仑兹力为f,在磁场中做圆周运动的半径为r,欲使微粒能进入小孔,半径r的取值范围为: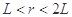
代入数据得: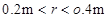 ①
①
(2) 由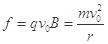 得:
得: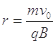 ②
②
对应微粒初速度,代入数据得:80m/s<v0<160m/s ③
欲使进入小孔的微粒与挡板一次相碰返回后能通过小孔,还必须满足条件:
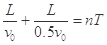 其中n=1,2,3,…… ④
其中n=1,2,3,…… ④
由③④可知,只有n=2满足条件,即有:v0=100m/s ⑤
(3)设微粒在磁场中做圆周运动的周期为T0,从水平进入磁场到第二次离开磁场的总时间为t,设t1、t4分别为带电微粒第一次、第二次在磁场中运动的时间,第一次离开磁场运动到挡板的时间为t2,碰撞后再返回磁场的时间为t3,运动轨迹如图所示,则有:
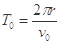 ⑥
⑥ 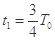 ⑦
⑦  ⑧
⑧  ⑨
⑨ 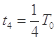 ⑩
⑩
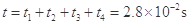 11
11
评分标准:①②③每式2分,④⑤每式2分 ⑥⑦⑧⑨⑩⑾共2分。
考点:本题考查了带电粒子在磁场中的运动、牛顿第二定律、向心力、带电粒子在电场中的运动。
本题难度:困难
4、填空题 放射源中有三种不同的粒子,其中一种不带电,另两种分别带正负电荷,置于磁场中,形成如图三条轨迹,则不带电的粒子的轨迹是______,带负电的粒子的轨迹是______.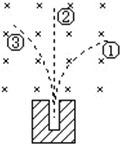
参考答案:由于磁场方向垂直纸面向里,根据左手定则,若粒子带正电,粒子向左偏转,粒子不带电,则粒子不发生偏转,当粒子带负电,则粒子向右偏转
故由图知,①带负电②不带电③带正电.
故答案为:②,①
本题解析:
本题难度:一般
5、简答题 在光滑绝缘的水平桌面上,有两个质量均为m,电量为+q的完全相同的带电粒子P1和P2,在小孔A处以初速度为零先后释放.在平行板间距为d的匀强电场中加速后,P1从C处对着圆心进入半径为R的固定圆筒中(筒壁上的小孔C只能容一个粒子通过),圆筒内有垂直水平面向上的磁感应强度为B的匀强磁场.P1每次与筒壁发生碰撞均无电荷迁移,P1进入磁场第一次与筒壁碰撞点为D,∠COD=θ,如图所示.延后释放的P2,将第一次欲逃逸出圆筒的P1正碰圆筒内,此次碰撞刚结束,立即改变平行板间的电压,并利用P2与P1之后的碰撞,将P1限制在圆筒内运动.碰撞过程均无机械能损失.设d=
πR,求:在P2和P1相邻两次碰撞时间间隔内,粒子P1与筒壁的可能碰撞次数.
附:部分三角函数值
| φ | | | | | | | | |
tanφ
3.08
1.73
1.00
0.73
0.58
0.48
0.41
0.36
0.32
|
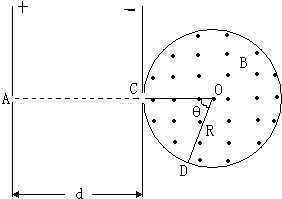
参考答案:粒子在磁场中匀速圆周运动的周期T=2πmqB,
? 由几何知识,得半径r=Rtanθ2=mvqB
? 从C到D的时间tCD=π-θ2πT
?P1、P2每次碰撞都应当在C点.
? 设P1在圆筒内转动了n圈和筒壁碰撞了K次后与P2相碰于C点,则K+1=2πnθ
? 所以两粒子每次碰撞的时间间隔t=tCD(K+1)=2πmqB?π-θ2π(k+1)=m(π-2πnk+1)qB(k+1)
? 在t 时间内,P2向左运动x再回到C,平均速度为v2
? t=2xv2=4xv≤4dv=5πR2v
? 由上述两式可得,5πR2v≥m(π-2πnk+1)qB(k+1)
? (k+1)mvqB(1-2nk+1)≤52R
? ?tannπk+1(k+1-2n)≤52
? 当?n=1,K=2、3、4、5、6、7?时符合条件,K=1、8、9…不符合条件
? 当?n=2,3,4….时,无论K等于多少,均不符合条件.
答:在P2和P1相邻两次碰撞时间间隔内,粒子P1与筒壁的可能碰撞次数为2、3、4、5、6、7.
本题解析:
本题难度:一般