1、计算题  [物理

参考答案：

本题解析：

本题难度：一般

2、简答题  两个分别具有动能E1=1MeV的氘核正面相碰，结果出现生成氦核（

参考答案：核反应方程为：21H+21H→32He+10n，
设21H，32He，10n的质量分别为ml、m2、m3，反应后的总动能为E．
由能量守恒得2El+2mlc2=（m2+m3）c2+E则：
E=2El+（2m1+m2一m3）c2=2×1+（2×2.0141+3.0160-1.0087）×931=5.25MeV
在碰撞的过程中，动量守恒，可得
m2υ2=m3υ3，又E2En=12m2υ2212m3υ33=m2(m3m2υ3)2m3υ23=m3m2
上式中只有En，E2都未知，而En+E2=E，则合分比定理将上式变为
E2+EnEn=m2m2+m3
故放出粒子的动能En=m2m2+m3(E2+En)=m2m2+m3E=3.01603.0160.1.0087×5.25=3.9MeV．
答：粒子的动能为3.9MeV．

本题解析：

本题难度：一般

3、选择题  如图光滑水平面上有质量相等的A和B两个物体，B上装有一轻质弹簧，B原来静止，A以速度v正对B滑行，当弹簧压缩到最短时，有：（?）

A．A的动量减小到最小，但不为零
B．A和B具有相同的速度
C．此时B的加速度达到最小
D．此时A和B的总动能达到最大

参考答案：B

本题解析：在压缩弹簧的过程中，没有机械能的损失，减少的动能转化为弹簧的弹性势能．在压缩过程中水平方向不受处力，动量守恒．则有当B开始运动时，A的速度等于v，所以没有损失动能．当B的速度v时，根据动量守恒定律有A的速度等于零，所以系统动能又等于初动能；而在AB速度相等时，此时弹簧压缩至最短，故弹簧的弹性势能最大，故动能应最小，故此时A的速度不为零，A错误；B正确；
因为此时弹簧的弹力最大，所以AB小球的加速度最大，不为零，C错误；
此时弹簧的弹性势能最大，所以动能最小，D错误
故选B
点评：题中A的动能转化为AB的动能及弹簧的弹性势能，而机械能守恒，故当弹性势能最大时，系统损失的机械能最多,弹簧压缩至最短，

本题难度：一般

4、简答题  如图所示，质量为M=3kg、长度为L=1.2m的木板静止在光滑水平面上，其左端的壁上有自由长度为L0=0.6m的轻弹簧，右端放置一质量为m=1kg的小物块，小物块与木块间的动摩擦因数为μ=0.4，今对小物块施加一个水平向左的瞬时冲量I0=4N?s，小物块相对于木板向左运动而压缩弹簧使弹性势能增大为最大值Emax，接着小物块又相对于木板向右运动，最终恰好相对静止于木板的最右端，设弹簧未超出弹性限度，并取重力加速度为g=10m/s2．求：
（1）当弹簧弹性势能最大时小物块速度v；
（2）弹性势能的最大值Emax及小物块相对于木板向左运动的最大距离Lmax．

参考答案：（1）由动量定理得I0=mv0
弹簧弹性势能最大时物块与木板的速度相同，则由动量守恒定律得 mv0=（m+M）v　
于是可解得：v=1m/s．
（2）由动量守恒定律和功能关系得
mv0=（m+M）u
物块相对于木板向左运动过程：12mv20=12（m+M）v2+μmgLmax+Emax　　　　　　
物块相对于木板向右运动过程：12mv20=12（m+M）u2+2μmgLmax
可解得：Emax=3J，Lmax=0.75m．
答：
（1）当弹簧弹性势能最大时小物块速度v是1m/s；
（2）弹性势能的最大值Emax为3J，小物块相对于木板向左运动的最大距离Lmax是0.75m．

本题解析：

本题难度：简单

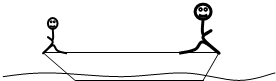
5、选择题  质量M=100kg的小船静止在平静水面上，船的两端站着质量分别为40kg和60kg的游泳者甲和乙，在同一水平线上甲向左乙向右同时相对于岸3m/s的水平速度跃入水中，如图所示，是小船的运动速率和方向为（　　）
A．小于1m/s，向左
B．大于1m/s，向左
C．小于1m/s，向右
D．大于1m/s，向右