微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
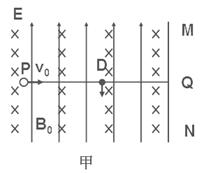
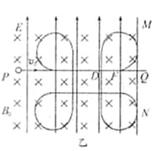
1、计算题 (18分)如图甲所示,竖直面MN的左侧空间存在竖直向上的匀强电场(上、下及左侧无边界)。一个质量为m、电量为q的可视为质点的带正电的小球,以大小为v0的速度垂直于竖直面MN向右作直线运动。小球在t=0时刻通过电场中的P点,为使小球能在以后的运动中竖直向下通过D点(P、D间距为L,且它们的连线垂直于竖直平面MN,D到竖直面MN的距离DQ等于L/π),经过研究,可以在电场所在的空间叠加如图乙所示随时间周期性变化的、垂直纸面向里的磁场,设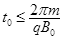 且为未知量。求:
且为未知量。求:
(1)场强E的大小;
(2)如果磁感应强度B0为已知量,试推出满足条件t1的表达式;
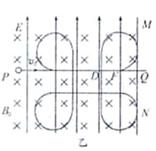
(3)进一步的研究表明,竖直向下的通过D点的小球将做周期性运动。则当小球运动的周期最大时,求出磁感应强度B0及运动的最大周期T的大小,并在图中定性画出此时小球运动一个周期的轨迹。
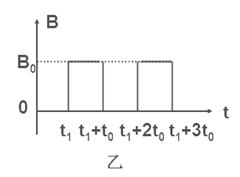
 ?
?
参考答案:(1)E=mg/q?(2)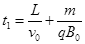
(3)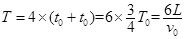 ?小球在电场中运动一个周期的轨迹图如图所示
?小球在电场中运动一个周期的轨迹图如图所示
本题解析:(1)小球进入电场,做匀速直线运动时 Eq=mg ①?(2分)
E=mg/q? ②?(2分)
(2)在t1时刻加磁场,小球在时间t0内做匀速圆周运动,设圆周运动周期为T0,半径为R 。
有: 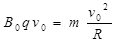 ③(2分) ?竖直向下通过D点应有:PF-PD=R?
③(2分) ?竖直向下通过D点应有:PF-PD=R?
即: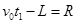 ?④(2分)?将④代入⑤式解得
?④(2分)?将④代入⑤式解得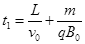 ?⑤(2分)
?⑤(2分)
(3)小球运动的速率始终不变,当R变大时,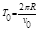 也增加,小球在电场中的运动周期T也增加。在小球不飞出电场的情况下,当T最大时有:DQ="2R" 即?
也增加,小球在电场中的运动周期T也增加。在小球不飞出电场的情况下,当T最大时有:DQ="2R" 即?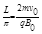 ⑥(2分)解得
⑥(2分)解得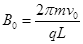 ?⑦(2分)
?⑦(2分)
结合乙图及轨迹图可知,小球在电场中运动的最大周期:
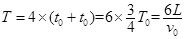 ?⑧(2分)
?⑧(2分)
小球在电场中运动一个周期的轨迹图如图所示(2分)
本题难度:一般
2、计算题 (16分)如图所示,在平面直角坐标系xoy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向里的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场.一粒子源固定在x轴上坐标为(-L,0)的A点.粒子源沿y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上坐标为(0,2L)的C点,电子经过磁场偏转后恰好垂直通过第一象限内与x轴正方向成15°角的射线ON(已知电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用).求:
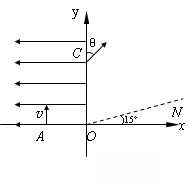
⑴匀强电场的电场强度E的大小;
⑵电子离开电场时的速度方向与y轴正方向的夹角θ;
⑶圆形磁场的最小半径Rmin.
参考答案:⑴E=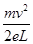 ;⑵θ=45°;⑶Rmin=
;⑵θ=45°;⑶Rmin=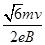 。
。
本题解析:⑴电子在从A运动到C的过程中,只受沿+x方向的电场力eE作用,故做类平抛运动,设其运动时间为t,因此在x方向上有:L= ?①
?①
在y方向上有:2L=vt?②
由①②式联立解得:E=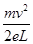
⑵根据类平抛运动的结论可知,电子离开电场时的速度的反向延长线将交于y方向位移的中点,即经过(-L,L)点,因此tanθ=1,θ=45°
⑶电子进入磁场后仅受洛伦兹力evCB作用,在磁场中做匀速圆周运动,设其轨道半径为r,根据牛顿第二定律有:evCB=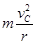 ?③
?③
根据几何关系可知:vC=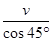 ?④
?④
根据题意作出电子的运动轨迹示意图如下图所示
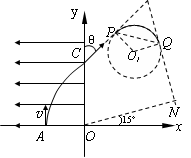
由图中几何关系可知,电子在磁场中偏转120°后垂直于ON射出,因此当图中PQ为圆形磁场的直径时其半径最小,即有:Rmin=rsin60°?⑤
由③④⑤式联立解得:Rmin=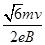
本题难度:困难
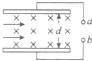
3、填空题 如图所示是等离子发电机示意图.磁感应强度B为O.5T,两极间距离为20cm,要使输出电压为220V.则等离子体的速度为______,a是电源的______极.
参考答案:电场强度E=Ud.
稳定时,洛伦兹力与电场力相等,则qvB=qE,解得:
v=EB=UBd=2200.5×0.2m/s=2200m/s.
根据左手定则知,正电荷向上偏转,负电荷向下偏转,则上极板带正电,a是电源的正极.
故答案为:2200m/s,正.
本题解析:
本题难度:简单
4、计算题 如图所示,竖直放置的金属薄板M、N间距为d.绝缘水平直杆左端从N板中央的小孔穿过,与M板固接,右端处在磁感应强度为B的匀强磁场中.质量为m、带电量为+q的中空小球P,套在水平直杆上,紧靠M板放置,与杆的动摩擦因数为μ.当在M、N板间加上适当的电压U后,P球将沿水平直杆从N板小孔射出,试问:
(1)此时M、N哪个板的电势高?它们间的电势差必须大于多少?
(2)若M、N间电压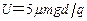 时,小球能沿水平直杆从N板中央小孔射入磁场,则射入的速率多大?若磁场足够大,水平直杆足够长,则小球在磁场中运动的整个过程中,摩擦力对小球做多少功?
时,小球能沿水平直杆从N板中央小孔射入磁场,则射入的速率多大?若磁场足够大,水平直杆足够长,则小球在磁场中运动的整个过程中,摩擦力对小球做多少功?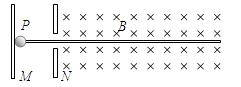
参考答案:(1)(8分)
若要小球P沿水平直杆从板间射出,必须使M板电势高于N板电势。? 2分
小球P能沿水平直杆从板间射出,必须使电场力大于小球所受的摩擦力,即
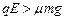 ? 2分
? 2分
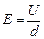 ? 2分
? 2分
故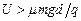 ? 2分
? 2分
即M板电势至少比N板高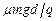
(2)(10分)
设P球射出电场时的速率为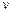 ,由动能定理得:
,由动能定理得:
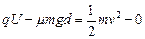 ? 2分
? 2分
即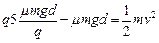 ?
?
解得: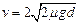 ? 2分
? 2分
小球P射入磁场后受到竖直向上的洛伦兹力作用,可能出现三种情况。
Ⅰ.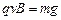 ,则小球不受摩擦力,做匀速直线运动。故摩擦力做功为零。1分
,则小球不受摩擦力,做匀速直线运动。故摩擦力做功为零。1分
Ⅱ.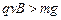 ,则直杆对小球有向下的压力,小球受摩擦力减速,当减速到洛仑兹力与重力大小相等后做匀速运动。设小球匀速时的速度为
,则直杆对小球有向下的压力,小球受摩擦力减速,当减速到洛仑兹力与重力大小相等后做匀速运动。设小球匀速时的速度为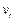 ,则
,则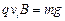 ? 1分
? 1分
设此过程中摩擦力做的功为W,由动能定理得: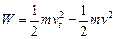 ? 1分
? 1分
即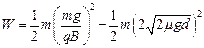
解得: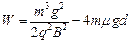 ? 1分
? 1分
上式中前后两项颠倒(即功的正负颠倒的),扣结论的1分
Ⅲ.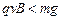 ,则直杆对小球有向上的支持力,
,则直杆对小球有向上的支持力,
小球受摩擦力减速,最终速度减为零。 1分
则摩擦力所做的功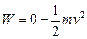
解得: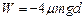 ? 1分
? 1分
功的正负颠倒,扣结论的1分
本题解析:略
本题难度:一般
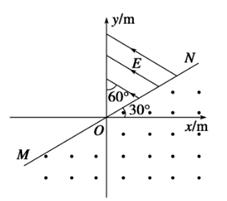
5、计算题 (12分)如图所示,在xoy平面内,直线MN与x轴正方向成30o角,MN下方是垂直于纸面向外的匀强磁场,MN与y轴正方向间存在电场强度E=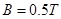 ×105N/C的匀强电场,其方向与y轴正方向成60o角且指向左上方,一重力不计的带正电粒子,从坐标原点O沿x轴正方向进入磁场,已知粒子的比荷
×105N/C的匀强电场,其方向与y轴正方向成60o角且指向左上方,一重力不计的带正电粒子,从坐标原点O沿x轴正方向进入磁场,已知粒子的比荷 =107C/kg,结果均保留两位有效数字,试问:
=107C/kg,结果均保留两位有效数字,试问:
(1)若测得该粒子经过磁场的时间t1= ,求磁感应强度的大小B;
,求磁感应强度的大小B;
(2)若测得该粒子经过磁场的时间t1= ,粒子从坐标原点开始到第一次到达y轴正半轴的时间t
,粒子从坐标原点开始到第一次到达y轴正半轴的时间t
(3)若粒子的速度v0=1.0×106m/s,求粒子进入电场后最终离开电场时的位置坐标
参考答案:(1)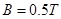 (2)
(2)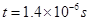 (3)
(3)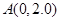
本题解析:(1)由几何关系可知: ,又
,又 联立可得
联立可得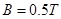
(2)设粒子在磁场中的运动半径为r,速度为v,由几何关系可知 ,POQ为等腰三角形,所以
,POQ为等腰三角形,所以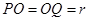 ,
,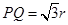 ,故
,故 ,
,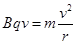 ,联立可得
,联立可得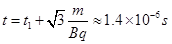
(3)粒子进入电场后做类平抛运动,设垂直于电场方向的距离为m,电场方向的距离为n,粒子离开电场时经过y轴,其位置坐标为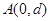 ,所以
,所以
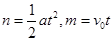 ,
, ,解得
,解得 ,又
,又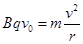 ,所以
,所以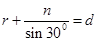 ,
,
联立可得

本题难度:一般