1、计算题  宽度为L，足够长的光滑倾斜导轨与水平面间夹角为θ，匀强磁场磁 感应强度为B，方向垂直于导轨向上，范围足够大，导轨的上端连着一个阻值为R的电阻，下端连着一个阻值为2R的电阻，导轨电阻不计。金属棒ab长为L，质量为m，电阻也为R，垂直地放在导轨上。在某一平行于导轨向上的恒力(图中未画出)的作用下，ab棒从静止开始沿导轨向上运动，最后达到稳定的运动状态。整个过程中，通过斜面底端电阻2R的最大电流为I，求：

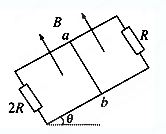
(1)通过ab棒的最大电流；(2)ab棒的最大加速度；(3)ab棒的最大速度。

参考答案：(1)3I?(2) 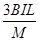?(3)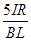

本题解析：(1)ab棒在外力F的作用下沿导轨向上做加速度a逐渐减小的加速运动，当a＝0时，速度v＝vm最大，此时电流也最大。
由电路结构知，此时，通过ab棒的电流为3I
(2)当速度v＝vm时，有F－3BIL－mgsinθ＝0 得F＝3BIL＋mgsinθ
刚开始时，v＝0，a＝am最大，
所以F－mgsinθ＝mam得am＝?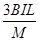
(3)a＝0时，v＝vm，ab棒的电动势E＝BLvm又E＝3I×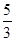R＝5IR
可得vm＝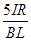

本题难度：一般

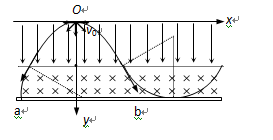
2、计算题  坐标原点O处有一放射源，它向xOy平面内的x轴下方各个方向发射速度大小都是v0的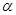粒子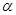，粒子的质量为m、电量为q；在0<y<d的区域内分布有指向y?轴正方向的匀强电场，在y≥d的区域内分布有垂直于xOy平面向里的匀强磁场，磁感应强度B=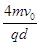，ab为一块很大的平面感光板，在磁场内平行于x轴放置，如图所示。测得进入磁场的a粒子的速率均为2v0，观察发现此时恰好无粒子打到ab板上。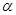（粒子的重力忽略不计）
(1)求电场强度的大小；
(2)求感光板到x轴的距离；
(3)磁感应强度为多大时所有粒子均能打到板上？并求出此时ab板上被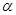粒子打中的区域的长度。

参考答案：（1）? (2) ?(3)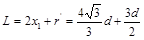

本题解析：（1）根据动能定理：? ------?(2分)
由于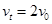?可得： 场强大小为? ------?(1分)
（2）对于沿x轴负方向射出的粒子进入磁场时与x轴负方向夹角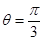? ------ (1分)
其在电场中沿x方向的位移??------ (2分)?
易知若此粒子不能打到ab板上，则所有粒子均不能打到ab板，因此此粒子轨迹必与ab板相切? ------ (2分)
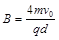根据洛伦兹力提供向心力------(1分)
可得其圆周运动的半径?------ (2分)
? ------ (1分)

（3）易知沿x轴正方向射出的粒子若能打到ab板上，则所有粒子均能打到板上。其临界情况就是此粒子轨迹恰好与ab板相切。可知此时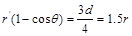? ------ (1分)
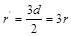? ------ (1分)

磁感应强度为原来的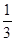，即当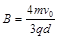恰好所有粒子均能打到板上? ------ (1分)
ab板上被打中区域的长度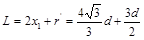? ------ (3分)

本题难度：一般

3、简答题  如图所示，水平放置的两平行金属板，它们之间的区域足够大，两板间有一个方向竖直向下的匀强电场，电场强度为E。现一带正电的粒子以速度v0沿垂直于场强方向由P点射入两板间的电场中，当粒子在电场中运动一段时间后它的速度大小达到2v0，这时将电场撤去，同时在两板间加一垂直于纸面方向的匀强磁场，过一段时间后又将磁场撤去，使该粒子恰好能通过P点沿着v0的反方向射出两板间的区域，不计粒子所受的重力作用。

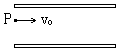
求：所加磁场的磁感强度的方向和大小

参考答案：磁场方向垂直于纸面向里?；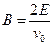

本题解析：
磁场方向垂直于纸面向里
设粒子在Q点的速度为2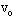
则有θ=60°

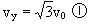
所以2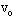的反向延长线与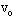的的正向延长线的夹角也为60°。过Q点做与直线AQ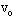，的正向延长线均相切的圆，两切点分别为Q、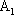。设圆的圆心为O，则直线O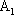，OQ均为半径，作直线OA，则OA为∠QA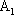的平分线，作过Q点AA1的垂线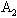Q。则Q为粒子做平抛运动过程中的竖直位移，设平抛运动的时间为t，粒子的质量为m，带电量为q。

本题难度：一般

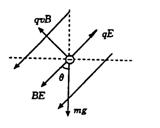
4、计算题  在地面上方的真空室内，存在匀强电场和匀强磁场。已知电场强度和磁感应强度的方向是相同的，电场强度的大小E ="4N/c,B=" 0.15T。今有一个带负电的质点以v = 20m/s的速度在此区域内沿垂直于电场强度方向做匀速直线运动，求此带电质点的电量与质量之比q/m以及磁场的所有可能方向。（g=9.8m/s2）

参考答案：由题意可知质点受的重力，电场力和洛伦兹力的合力必为零。由此推知三力在同一竖直平面内，如图所示由平衡条件得



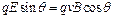
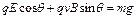
解得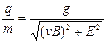代入数据得：q/m = 1.96C/kg，?
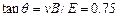，所以，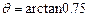
即磁场是沿与重力方向成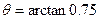，且斜向向下的一切方向。

本题解析：略

本题难度：简单

5、计算题  如图所示，质量M=0.01kg的导体棒ab，垂直放在相距l=0.1m的平行光滑金属导轨上。导轨平面与水平面的夹角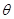=30°，并处于磁感应强度大小B=5T、方向垂直于导轨平面向下的匀强磁场中。左侧是水平放置的平行金属板，它的极板长s=0.1m，板间距离d=0.01m。定值电阻R=2Ω，Rx为滑动变阻器的阻值，不计其它电阻。

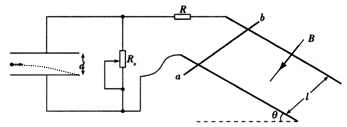
（1）调节Rx＝2Ω，释放导体棒，当棒沿导轨匀速下滑时，求通过棒的电流I及棒的速率v
（2）改变Rx ，待棒沿导轨再次匀速下滑后，将质量m=10-8kg、电量q=10-4C的带正电的粒子从两金属板中央左侧以v0=103 m/s水平射入，（不计粒子的重力），若它恰能从下板右边缘射出，求此时的Rx.

参考答案：（1）0.1A，0.8m/s（2）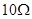

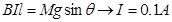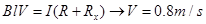本题解析：（1）根据受力分析可得：?（３分）
　　　（３分）
（２）根据牛顿第二定律可得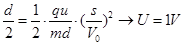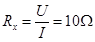：　。（３分）
点评：由电磁感应定律求电动势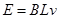、闭合电路欧姆定律求电流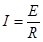，由导体棒受力平衡求速度，由带电粒子的匀速通过电容器求电压，结合闭合电路求速度．

本题难度：简单