|
|
|
高考物理高频考点《匀变速直线运动》试题强化练习(2017年最新版)(十)
2017-09-25 07:23:40
来源:91考试网
作者:www.91exam.org 【 大 中 小】
|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 (19分)如图所示的传送带装置,长度为4 m,与水平方向之间的夹角为37°,传送带以0.8 m/s的速度匀速运行,从流水线上下来的工件每隔2 s有一个落到A点(可认为初速度为零),工件质量为1 kg.经传送带运送到与B等高处的平台上,再由工人运走.已知工件与传送带之间的动摩擦因数为μ=0.8,sin 37°=0.6,cos 37°=0.8,g=10 m/s2.求:

(1)每个工件从落上传送带的A点开始到被传送至最高点B所经历的时间;
(2)传送带对每个工件所做的功;
(3)由于传送工件,传送带的动力装置需增加的功率.
参考答案:(1)6 s (2)24.32 J(3)14.72 W
本题解析:(1)工件刚放上传送带时的加速度为
a=μgcos 37°-gsin 37°=0.4 m/s2?(2分)
当工件速度达v=0.8 m/s时,工件相对传送带静止
工件加速的时间t1= = = s=2 s? (1分) s=2 s? (1分)
加速运动的位移
s1= at12= at12= ×0.4×22 m=0.8 m? (1分) ×0.4×22 m=0.8 m? (1分)
在AB段匀速运动的位移为
s2=4 m-0.8 m=3.2 m? (1分)
所用的时间为t2= = = s=4 s? (1分) s=4 s? (1分)
总时间为t=t1+t2=6 s? (1分)
(2)由动能定理得
W-mgLsin 37°= mv2?(3分) mv2?(3分)
W=mgLsin 37°+ mv2 mv2
=1×10×4×0.6 J+ ×1×0.82 J=24.32 J?(2分) ×1×0.82 J=24.32 J?(2分)
(3)因工件在AB段上加速运动的时间为2 s,所以在位移xt内总是有一个工件位于传送带上,该工件对传送带的滑动摩擦力为Ff1=mgμcos 37°=6.4 N (2分)
工件在AB段上匀速运动过程中,因前后两工件相隔时间为2 s,两工件之间的距离为2×0.8 m=1.6 m,所以这段距离内始终有两个工件位于传送带上,每个工件对传送带的摩擦力为Ff2=mgsin 37°=6 N ?(3分)
传送带动力装置需增加的功率为
P=(Ff1+2Ff2)v=18.4×0.8 W=14.72 W?(2分)
本题难度:一般
2、选择题 甲、乙两物体同时由同一地点向同一方向作直线运动,其υ-t图象如图所示,下列说法正确的是( )
A.20s末甲、乙两物体相距最远
B.前40s内甲、乙两物体间的距离逐渐减小,40s末乙追上甲
C.前40s内甲、乙两物体间距离一直在增大,40s末达到最大
D.前40s内甲、乙两物体间的距离先增大后减小,40s末乙追上甲
| 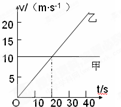
参考答案:A、速度相等时,甲乙两物体相距最远.故A正确,C错误.
B、前40s内,两物体的距离先增大,后减小,40s末两者的位移相等,乙追上甲.故B错误,D正确.
故选AD.
本题解析:
本题难度:一般
3、选择题 某物体做匀变速直线运动,其位移与时间的关系为x=0.5t+t2(m),则当物体速度为3 m/s时,物体已运动的时间为( ).
A.6 s
B.3 s
C.2.5 s
D.1.25 s
|
参考答案:D
本题解析:根据x=v0t+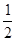 at2=0.5t+t2知,初速度v0=0.5m/s,加速度a=2m/s2.根据速度时间公式v=v0+at得,
at2=0.5t+t2知,初速度v0=0.5m/s,加速度a=2m/s2.根据速度时间公式v=v0+at得,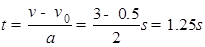 ,故D正确.
,故D正确.
考点:匀变速运动的规律.
本题难度:一般
4、选择题 物体沿光滑的斜面由静止开始匀加速下滑,在第3秒内的位移是2.5m,那么它的( )
A.加速度是0.5m/s2
B.第3S末的速度是2.5m/s
C.在前3秒内的位移是4.5m
D.ns内的位移n2m
参考答案:由中时刻的瞬时速度等于这段时间内的平均速度,所以第3秒内的位移是2.5m,则有第2.5秒的瞬时速度为xt=2.51m/s=2.5m/s
A、v=at?可知,a=vt=2.52.5m/s2=1m/s2,故A错误;
B、第3S末的速度为v=at=1×3m/s=3m/s,故B错误;
C、前3秒内的位移是x=12at2=12×1×32m=4.5m,故C正确;
D、由 x=12at2公式可得,ns内的位移为n22m,故D错误;
故选:C
本题解析:
本题难度:简单
5、计算题 甲、乙两个同学在直跑道上练习4×100 m接力跑,如图所示,他们在奔跑时有相同的最大速度。乙从静止开始全力奔跑需跑出25 m才能达到最大速度,这一过程可看做匀变速运动。现在甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出。若要求乙接棒时奔跑达到最大速度的80%,则:
(1)乙在接力区需奔出多少距离?
(3)乙应在距离甲多远时起跑?
参考答案:解:(1)设两人的最大速度为v,则v2=2ax,(0.8v)2=2ax",得x"=16 m
(2)设乙在距甲为X0处开始起跑,到乙接棒时跑过的距离为x",贝有vt=x0+x",且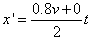 ,解得x0=24 m
,解得x0=24 m
本题解析:
本题难度:一般
An empty sack cannot stand upright. 空袋难站立. /有理走遍天下,无理寸步难行.

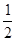 at2=0.5t+t2知,初速度v0=0.5m/s,加速度a=2m/s2.根据速度时间公式v=v0+at得,
at2=0.5t+t2知,初速度v0=0.5m/s,加速度a=2m/s2.根据速度时间公式v=v0+at得,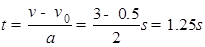 ,故D正确.
,故D正确.
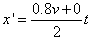 ,解得x0=24 m
,解得x0=24 m