1、选择题  光滑地面上放着两钢球A和B，且mA＜mB，B上固定着一轻弹簧，如图所示，现在A以速率v0碰撞静止的B球，有：(? )?

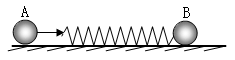
A．当弹簧压缩量最大时，A、B两球的速率都最小；
B．当弹簧恢复原长时，A球速率为零；
C．当A球速率为零时，B球速率最大；
D．当B球速率最大时，弹簧的势能为零；

参考答案：D

本题解析：当两球速度相等时压缩量最大，据动量守恒定律有mAv0=(mA+mB)vAB，则解得vAB=mAv0/(mA+mB)，可见B球速度从0开始增加，所以A选项错误；据mAv0=mAvA+mBvB可知，当弹簧回复原长时，A球的速度可能与初速度反向，也可能与初速度同向，不可能为0，但此时B球的速度最大，所以B、C选项错误，而D选项正确。

本题难度：一般

2、简答题  物理选修3-5
（1）太阳内部发生的核反应主要是轻核的聚变，太阳中存在的主要元素是氢，氢核的聚变反应可以看做是4个氢核（

参考答案：（1）①根据核反应方程质量数和核电荷数守恒得：411H→24He+210e
②△m=4mP-mα-2me=4×1.0073u-4.0015u-2×0.00055u=0.0266?u
△E=0.0266?u×931.5MeV/u=24.8?MeV?
（2）设冰壶的质量为m，冰壶碰撞过程中动量守恒，根据动量守恒定律得：
mv0=mv1+mv2
解得：v2=0.3m/s
答：（1）①该热核反应方程为?411H→24He+210e
②一次这样的热核反应过程中释放出?24.8?MeV能量．
（2）0.3m/s

本题解析：

本题难度：一般

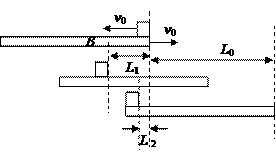
3、简答题  如图所示，一质量为M、长为L的长方形木板B放在光滑的水平地面上，在其右端放一质量为m的小木块A，m＜M。现以地面为参照系，给A和B以大小相等、方向相反的初速度(如图1)，使A开始向左运动，B开始向右运动，但最后A刚好没有滑离B板，以地面为参照系。

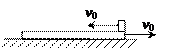
(1)若已知A和B的初速度大小为V0， 求它们最后的速度大小和方向。
(2)若初速度的大小未知，求小木块A向左运动到达的最远处(从地面上看)离出发点的距离。

参考答案：V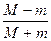＝。方向向右 。L1=。

本题解析：用能量守恒定律和动量守恒定律求解。

A刚好没有滑离B板，表示当A滑到B板的最左端时，A、B具有相同的速度，设此速度为V， A和B的初速度的大小为V0，则据动量守恒定律可得：?MV0－mV0="(m+m)V?"
解得：V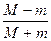＝。 V0，方向向右 。
对系统的全过程，由能量守恒定律得：
Q=fL=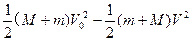
对于A fL1=
由上述二式联立求得L1=。

本题难度：简单

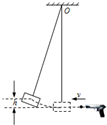
4、简答题  如图所示，一质量M=1.0kg的砂摆，用轻绳悬于天花板上O点．另有一玩具枪能连续发射质量m=0.01kg，速度v=4.0m/s的小钢珠．现将砂摆拉离平衡位置，由高h=0.20m处无初速度释放，恰在砂摆向右摆到最低点时，玩具枪发射的第一颗小钢珠水平向左射入砂摆，二者在极短时间内达到共同速度．不计空气阻力，取g=10m/s2．
（1）求第一颗小钢珠射入砂摆前的瞬间，砂摆的速度大小v0；
（2）求第一颗小钢珠射入砂摆后的瞬间，砂摆的速度大小v1；
（3）第一颗小钢珠射入后，每当砂摆向左运动到最低点时，都有一颗同样的小钢珠水平向左射入砂摆，并留在砂摆中．当第n颗小钢珠射入后，砂摆能达到初始释放的高度h，求n．

参考答案：（1）砂摆从释放到最低点，由动能定理：
Mgh=12Mv02-0，解得：v0=

本题解析：

本题难度：一般

5、计算题  如图所示，半径为R，内表面光滑的半球形容器放在光滑的水平面上，容器左侧靠着竖直墙壁，一个质量为m的小球，从容器顶端A无初速释放，小球能沿球面上升的最大高度距球面底部B的距离为3R/4，小球的运动在竖直平面内。求：
（1）容器的质量M
（2）竖直墙作用于容器的最大冲量。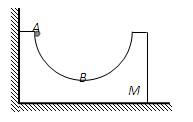

参考答案：（1）在A球释放到B点时，M未动，对A由机械能守恒有：
mgR=mv02（2分）
此后A继续向右运动，但B在A给它作用力情况下，离开墙壁向右运动，
对A、B系统：由水平方向动量守恒得：
mv0="(M+m)" v1（2分）
由机械能守恒得：
mg·R=mv02－(M+m) v12（2分）
由以上三式解得v0=?M=3m（2分）
（2）由于在A球释放到B点时，M未动，此后M离开墙壁向右运动，所以对A、B系统来讲，由动量定理知，竖直墙对容器的最大冲量为A球水平动量的变化，
即Im=mv0
代入v0得Im=m（2分）

本题解析：略

本题难度：一般