1、简答题  一组人乘太空穿梭机，去修理位于离地球地表面0.6×106m的圆形轨道上的哈勃太空望远镜H，机组人员使穿梭机S进入与H相同的轨道并关闭推动火箭，而望远镜则在穿梭机前方数公里外，如图所示（已知：地球半径为6.4×106m）
（1）在穿梭机内，一质量为70kg的人的视重是多少？
（2）①计算轨道上的重力加速度的值；
②计算穿梭机轨道上的速率和周期．
（3）穿梭机需首选进入半径较小的轨道，才有较大的角速度以追上望远镜，用上题的结果判断穿梭机要进入较低轨道时应增加还是减少其原有速率，解释你的答案．

参考答案：
（1）穿梭机内的人处于完全失重状态，故视重为零．
（2）由mg=GMmR2
得：gR2=GM
轨道处的重力角速度g′则有
mg′=GMm(R+h)2
解得：
g′=R2(R+h)2g
又：
GMm(R+h)2=mv2R+h
解得：
v=

本题解析：

本题难度：一般

2、计算题  月球质量是地球质量的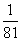，月球的半径是地球半径的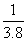.月球上空高500m处有一质量为60kg的物体自由下落。求：
(1)它落到月球表面所需要的时间是多少?
(2)它在月球上的重力和质量跟在地球上有没有不同(g地=9.8m/s2)?

参考答案：解：（1）设月球表面的“重力加速度”为g月，物体在月球上的“重力”等于月球对它的引力
mg月=G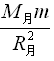，mg地=G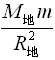两式相比得：
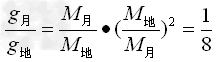×3.82≈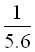
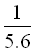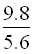即g月=g地=m/s2≈1.75m/s2
所以物体在月球上空500m处自由落下到达月球表面所需要的时间
t=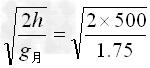s≈24s
（2）物体的质量是恒定的，在月球和地球上的质量都是60kg，但在月球和地球上的重力不同
G地=mg月=60×9.8N=558N
G月=mg月=60×1.75N=105N

本题解析：

本题难度：一般

3、选择题 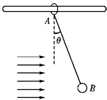 如图所示，水平细杆上套一环A，环A与球B间用一轻质绳相连，质量分别为mA、mB，由于球B受到风力作用，环A与球B一起向右做匀速运动．已知细绳与竖直方向的夹角为θ，则下列说法中正确的是
A.杆对环A的支持力随着风力的增加而增加
B.风力增大时，轻质绳对球B的拉力保持不变
C.球B受到的风力F为mBgtanθ
D.环A与水平细杆间的动摩擦因数为

参考答案：C

本题解析：分析：以环A和球B整体为研究对象，分析支持力随着风力的增加如何变化，求解动摩擦因数．以B球为研究对象，分析球B受到的风力F和轻质绳对球B的拉力如何变化．
解答：A、以整体为研究对象，分析受力如图1所示，根据平衡条件得知：杆对环A的支持力N=（mA+mB）g，所以杆对环A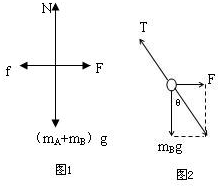的支持力保持不变．故A错误．
B、C以B球为研究对象，分析受力如图2所示，由平衡条件得到：轻质绳对球B的拉力T=，风力F=mBgtanθ，风力F增大时，θ增大，cosθ减小，T增大．故B错误，C正确．
D、由图1得到f=F，环A与水平细杆间的动摩擦因数为μ=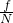=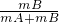tanθ．故D错误．
故选C
点评：本题是两个物体的平衡问题，要灵活选择研究对象．几个物体的速度相同时，可以采用整体法研究．

本题难度：困难

4、简答题  为了探测某星球，宇航员乘飞船沿该星球的近地圆形轨道（可以认为飞船运行半径等于星球半径）绕该星球运行一周，所用时间为T．降落至该星球后，又做了如下两个实验：
实验1：将一质量为m的小球挂在弹簧秤下，静止时读数为F；
实验2：将该小球以一定初速度竖直上抛，经过时间t小球落回原处；
若不考虑该星球的自转，请回答下列问题：
（1）由实验1所给物理量，求出该星球表面的重力加速度g；
（2）求实验2中竖直上抛小球的初速度V0；
（3）若万有引力常量为G，求该星球的半径R和质量M．

参考答案：（1）由F=mg得该星球表面的重力加速度g=Fm
（2）小球上升时间和下落时间相等，均为t2，
则：v0=gt2=Ft2m
（3）在该星球表面，物体重力等于它所受万有引力，有：mg=GmMR2
设飞船的质量为m"，飞船绕行时，飞船所受万有引力提供向心力，则：Gm′MR2═m′(2πT)2R
解得：R═FT24π2m
M=FR2mG=F3T416π4Gm3
答：（1）该星球表面的重力加速度g为Fm；（2）竖直上抛小球的初速度为Ft2m；（3）该星球的半径R为FT24π2m，质量M为M=F3T416π4Gm3．

本题解析：

本题难度：一般

5、填空题  已知月球绕地球运动周期T和轨道半径r，地球半径为R,万有引力常量为G.则地球的质量为       ，地球的平均密度为         。

参考答案：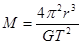  

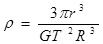
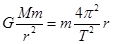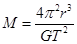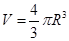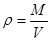本题解析：地球对月球的万有引力充当向心力，，所以根据万有引力定律以及牛顿第二定律可得，解得：，地球的体积，，根据可得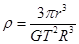
考点：考查了万有引力定律的应用
点评：基础题，关键对公式的灵活应用，计算时需要细心

本题难度：一般