1、填空题  质量相等的两质点分别做匀速圆周运动，若在相等时间内通过的弧长之比为2：3，而转过的角度之比为3：2，则两质点周期之比=______，向心加速度之比=______，向心力之比为=______．

参考答案：在相同时间内，它们通过的弧长之比 SA：SB=2：3，由v=st公式可知，线速度之比vA：vB=SA：SB=2：3．
在相同时间内，转过的角度之比φA：φB=3：2，
由公式ω=θt可知角速度之比ωA：ωB=φA：φB=3：2．
由T=2πω得周期之比TA：TB=ωB：ωA=φB：φA=2：3．
向心加速度之比a=ωAvAωBvB=32×23=11
向心力F=ma，质量相等，则向心力之比等于向心加速度之比1：1；
故答案为：2：3；1：1；1：1．

本题解析：

本题难度：简单

2、计算题  如图所示，杆长为L，杆的一端固定一个质量为m的小球，杆的质量忽略不计，整个系统绕杆的另一端在竖直平面内做圆周运动，求：
(1)?小球在最高点A时速度vA为多大时，才能使杆对小球m的作用力为零？
(2) 小球在最高点A时，杆对小球的作用力F为拉力，且大小F=mg,则小球此时的速度是多少？
(3) 如m=0.50kg，L=0.5m，vA=0.4m/s，则在最高点A时，杆对小球的作用力是多大？是推力还是拉力？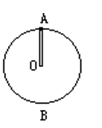

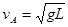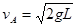参考答案：(1) (2) (3) F=4.84N

本题解析：(1),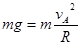
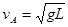
(2)
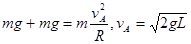
(3)最高点，向心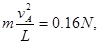力重力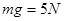，杆对球的作用力为推力，F=4.84N
本题考查圆周运动的规律应用,能通过最高点的临界情况是只有重力提供向心力,在第三问中可以设杆的作用力向下,根据合力提供向心力,求出杆的作用力为正值方向向下,为负值方向向上

本题难度：一般

3、选择题  两个靠近的天体称为双星，它们以两者连线上某点O为圆心做匀速圆周运动，其质量分别为m1、m2，如图所示，以下说法正确的是(? )

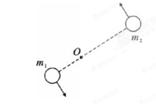
A．它们的角速度相同
B．向心力与质量成正比
C．线速度与质量成反比
D．轨道半径与质量成正比

参考答案：AC

本题解析：在双星问题中它们的角速度相等，设两星之间的距离为L，则有：①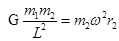?②联立①②可得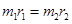：，即轨道半径和质量成反比，同时由万有引力公式可知向心力与质量的乘积成正比．综上分析可知，BD错误，AC正确．
故选AC．
点评：解决问题时要把握好问题的切入点．如双星问题中两卫星的向心力相同，角速度相等．

本题难度：简单

4、选择题  物体做匀速圆周运动时，下列说法正确的是（　　）
A．物体的加速度恒定
B．物体所受合力必须等于零
C．物体的线速度恒定
D．物体所受合力的大小不变

参考答案：匀速圆周运动的过程中，线速度的大小不变，但方向改变，所以线速度改变，角速度不变．所受合力提供向心力，大小不变，方向改变，是个变力，向心加速度方向始终指向圆心，是个变量，故ABC错误，D正确；
故选D．

本题解析：

本题难度：简单

5、计算题  如图所示，图中的装置可测量子弹的速度，其中薄壁圆筒半径为R，圆筒上的a、b两点是一条直径上的两个端点（图中OO′为圆筒轴线）。圆筒以速度v竖直向下匀速运动。若某时刻子弹沿图示平面正好水平射入a点，且恰能经b点穿出。

（1）若圆筒匀速下落时不转动，求子弹射入a点时速度的大小；
（2）若圆筒匀速下落的同时绕OO匀速转动，求圆筒转动的角速度条件。

参考答案：(1)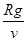  (2)w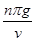＝，n＝1、2、3、……

本题解析：
（1）子弹做平抛运动，水平方向：2R＝v0t,
竖直方向：vt＝gt2,
代入解得：v0＝.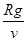
（2）圆筒转动的角度一定是2p的整数倍：
2pn＝wt（n＝1、2、3、……）
而下落时间：t＝,
代入得：w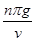＝，n＝1、2、3、……

本题难度：困难