1、选择题  A、B、C三个物体放在旋转圆台上，都没有滑动，如图所示。静摩擦因素均为μ，A的质量为2m，B、C的质量均为m，A、B离轴为R，C离轴为2R.当圆台旋转时，下列说法错误的是：（?）
A. 当圆台匀速转动时，C物的向心加速度最大
B. 当圆台匀速转动时，B的静摩擦力最小
C．当圆台转速逐渐增加时，A受到的静摩擦力始终指向圆台的转轴
D．当圆台转速增加时，C比A先滑动

参考答案：C

本题解析：先对三个物体进行运动分析与受力分析，找出向心力来源，根据向心力公式求出摩擦力，再求出物体受最大静摩擦力时的临界角速度．
解：三个物体都做匀速圆周运动，合力指向圆心，对任意一个受力分析，如图

支持力与重力平衡，F合=f=F向,由于a、b、c三个物体共轴转动，角速度ω相等，
根据题意，rc=2ra=2rb=r,由向心力公式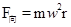，得三物体的向心力分别为：
Fa=2mω2r
Fb=mω2r=mω2r
Fc=mω2（2r）=2mω2r
故A、B正确；故C正确；
对任意一物体，由于摩擦力提供向心力，有μmg=mω2r当ω变大时，所需要的向心力也变大，当达到最大静摩擦力时，物体开始滑动，当转速增加时，A、C所需向心力同步增加，且保持相等，但因C的最大静摩擦力小，C比A先滑动．故D正确．
故选C．
点评：本题可从三个物体中选择任意一个物体，建立物理模型后分析比较，而不需要对三个物体分别分析！难度适中．

本题难度：一般

2、选择题  某公园里的过山车驶过离心轨道的最高点时，乘客在座椅里面头朝下，人体颠倒，若轨道半径为R，人体重为mg，要使乘客经过轨道最高点时对座椅的压力等于自身的重力，则过山车在最高点时的速度大小为

[? ]
A．0
B．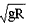
C．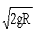
D．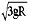

参考答案：C

本题解析：

本题难度：一般

3、填空题  如图所示，半径为R的半球形碗内表面光滑，一质量为m的小球以角速度ω在碗内一水平面做匀速圆周运动，则该平面离碗底的距离h=______．

参考答案：

小球靠重力和支持力的合力提供向心力，小球做圆周运动的半径为r=Rsinθ，根据力图可知tanθ=F向mg=m?Rsinθω2mg
解得cosθ=gRω2．所以h=R-Rcosθ=R-gω2．
故答案为：R-gω2．

本题解析：

本题难度：一般

4、选择题  轻杆一端固定在光滑水平轴O上，另一端固定一质量为m的小球，如图所示。给小球一
初速度，使其在竖直平面 内做圆周运动，且刚好能到达最高点P，下列说法正确的是

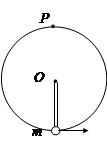
A．小球在最高点时对杆的作用力为零
B．小球在最高点时对杆的作用力为mg
C．若增大小球的初速度，则在最高点时球对杆的力一定增大
D．若增大小球的初速度，则在最高点时球对杆的力可能增大

参考答案：BD

本题解析：A、B以小球为研究对象，设在最高点时杆对小球的作用力大小为F，方向竖直向上．小球刚好能通过最高点P，速度为零，根据牛顿第二定律得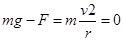，，即有F=mg，再由牛顿第三定律得到，小球在最高点时对杆的作用力也为mg；B正确．
C、由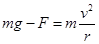得到?，增大小球的初速度，在最高点时球对杆的力为先减小后反向增大；错误
D、若增大小球的初速度，当时，F＜0，F方向竖直向下，杆对小球施加拉力，则球对杆也拉力作用；正确
故选BD
点评：小球在竖直平面内做圆周运动通过最高点的最小速度为0，当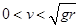时杆对球有支持力，当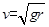时，杆对球的作用力为0，当时杆对球有向下的拉力。

本题难度：一般

5、计算题  长为L的轻杆一端安在光滑固定转动轴O上，另一端固定有一只质量为m的小球A（视为质点）。给小球一个初速度，使它在竖直面内绕O做圆周运动，已知：当小球到达最高点时，小球对杆的压力大小为小球重力的1/4；小球通过最低点时速度大小为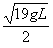。求：
（1）小球通过最高点时的速率V。
（2）小球通过最低点时对杆的拉力大小F。

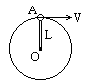
参考答案：解：（1）小球在最高点的受力如图：小球在最高点的向心力由mg和N的合力来提供，由牛顿第二定律得

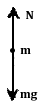
mg－N=m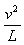
N=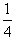mg
解得：v=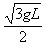
（2）小球在最低点时，杆对小球的拉力为F′，受力如图。同理由牛顿第二定律得：

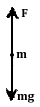
F′－mg=m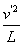
v"=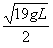
得：F′=5.75mg
由牛顿第三定律可知，小球对杆的拉力大小F=5.75mg

本题解析：

本题难度：一般