1、计算题  如图所示，矩形线圈abcd在磁感强度B=2T的匀强磁场中绕轴OO′，以角速度ω=10πrad／s匀速转动，线圈匝数N=10，总电阻为r=1Ω。ab=0.2m，bc=0.3m，负载电阻R=14Ω。求：
（1）电阻R在0.2s内所发出的热量；
（2）0.05s内流过电阻R的电量（设线圈从图示位置开始计时）；
（3）伏特表的示数；
（4）框转到图示位置时穿过闭合回路磁通量的变化率。

参考答案：（1）Q=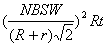=8.96J
（2）0.05秒正好是四分之一周期，线框转到中性面位置，所以q=N=0.08 C
（3）U=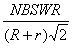=24.87 V
（4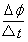）=BSω=3.77 wb/s

本题解析：

本题难度：困难

2、简答题  如图甲所示，在一个正方形金属线圈区域内，存在着磁感应强度B随时间变化的匀强磁场，磁场的方向与线圈平面垂直．金属线圈所围的面积S=200cm2，匝数n=1000，线圈电阻r=1.0Ω．线圈与电阻R构成闭合回路，电阻R=4.0Ω．匀强磁场的磁感应强度随时间变化的情况如图乙所示，求：
（1）在t=2.0s时刻，通过电阻R的感应电流的大小；
（2）在t=2.0s时刻，电阻R消耗的电功率；
（3）0～6.0s内整个闭合电路中产生的热量．

参考答案：（1）根据法拉第电磁感应定律，0～4.0s时间内线圈中磁通量均匀变化，产生恒定的感应电流．
? t1=2.0s时的感应电动势E1=n△Φ△t1=n(B4-B0)S△t1
? 根据闭合电路欧姆定律，闭合回路中的感应电流I1=E1R+r
? 解得?I1=0.2A?
? （2）在t=2.0s时刻，电阻R消耗的电功率P=I12R=0.16W．
?（3）根据焦耳定律，0～4.0s内闭合电路中产生的热量
? Q1=I12（r+R）△t1=0.8?J?
? 由图象可知，在4.0s～6.0s时间内，线圈中产生的感应电动势E2=n△Φ2△t2=nΦ6-Φ4△t2
? 根据闭合电路欧姆定律，t2=5.0s时闭合回路中的感应电流I2=E2R+r=0.8A
? 闭合电路中产生的热量 Q2=I22（r+R）△t2=6.4J
?故0～6.0s内整个闭合电路中产生的热量Q=Q1+Q2=7.2J．
答：（1）在t=2.0s时刻，通过电阻R的感应电流的大小为0.2A；
? （2）在t=2.0s时刻，电阻R消耗的电功率为0.16W；
? （3）0～6.0s内整个 闭合电路中产生的热量为7.2J．

本题解析：

本题难度：一般

3、计算题  电路如图所示，电源电动势E=9V，内阻r=l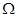，R2=2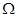，灯A是“6V，6W”，灯B是“4V，4W”求：

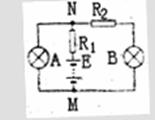
（1）如果要使B灯正常发光，R1应是多大?
（2）这时灯A的实际功率多大?

参考答案：（1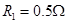） （2）

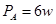
本题解析：B灯正常发光时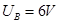，电流?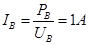
灯泡B和电阻R2 串联，总电压?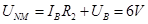
灯泡A与灯泡B和电阻R2 ?并联，所以A的电压也等于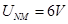，A正常发光,所以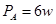?3分
通过A的电流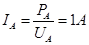
电路总电流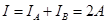?（4分）
?

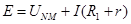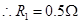
本题难度：一般

4、选择题  供电电路电源的输出电压为U1，线路损失电压为U2，用电器得到的电压为U3，总电流为I，线路导线的总电阻为R，若要计算线路的功率损失，不可用的公式有
[? ]
A．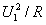
B．IU2
C．I2R
D．
E．I(U1-U3)

参考答案：A

本题解析：

本题难度：一般

5、选择题  某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在了同一坐标上，如图所示.根据图线可知

A．反映Pr变化的图线是c
B．电源电动势为8 V
C．电源内阻为2 Ω
D．当电流为0.5 A时，外电路的电阻为6 Ω

参考答案：ACD

本题解析：根据直流电源的总功率PE=EI，内部的发热功率Pr=I2r，输出功率PR=EI-I2r，可知反映Pr变化的图线是c，反映PE变化的是图线a，反映PR变化的是图线b，A正确；图线a的斜率等于电源的电动势，由得到E=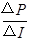=4V，B错误；当I=2A时，Pr=8W，由公式Pr=I2r得，r=2Ω，C错误；当电流为0.5A时，由图读出电源的功率PE=2W．由PE代入得到，R=6Ω，D正确。

本题难度：一般