1、简答题  如图，质量为m=10g，电量为q=10-4C的带正电小球用长为L=0.3m的绝缘细线系于O点放在匀强电场中，静止时悬线与竖直方向夹角θ=600，求：
（1）电场强度；
（2）若通过外力做功将带电小球缓慢拉至竖直方向的最低点并使
悬线拉紧，而小球最终处于静止状态，问外力需做多少功？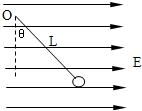

参考答案：（1）分析带电小球的受力情况如图所示，可得：
qE=mgtanθ
解得E=mgtanθq=10×10-3×10×

本题解析：

本题难度：一般

2、计算题  如图所示的坐标系，x轴沿水平方向，y轴沿竖直方向．在x轴上方空间的第一、第二象限内，既无电场也无磁场，在第三象限内存在沿y轴正方向的匀强电场和垂直于xOy平面向里的匀强磁场，在第四象限内存在沿y轴负方向、场强大小与第三象限电场强度相等的匀强电场．一质量为m、电荷量为q的带电质点，从y轴上y＝h处的P1点以一定的水平初速度沿x轴负方向进入第二象限，然后经过x轴上x＝－2h处的P2点进入第三象限，带电质点恰能做匀速圆周运动，之后经过y轴上y＝－2h处的P3点进入第四象限．试求：

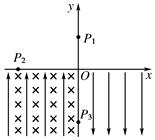
(1)第三象限空间中电场强度和磁感应强度的大小．
(2)带电质点在第四象限空间运动过程中的最小速度．

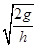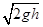参考答案：(1)　　(2)，方向沿x轴正方向

本题解析：(1)质点从P2到P3的运动过程中，重力与电场力平衡，洛伦兹力提供向心力．则qE＝mg
解得E＝
在第二象限内从P1到P2的运动过程是只在重力作用下的平抛运动，即h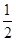＝gt2,2h＝v0t，vy＝gt
那么质点从P2点进入复合场时的速度为
v＝＝2
方向与x轴负方向成45°角，运动轨迹如图所示．

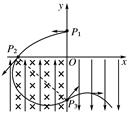
质点在第三象限内满足qvB＝m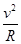
由几何知识可得：(2R)2＝(2h)2＋(2h)2，所以B＝.
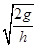(2)质点进入第四象限，水平方向做匀速直线运动，竖直方向做匀减速直线运动．当竖直方向的速度减小到零时，此时质点速度最小，也就是说最小速度vmin是v在水平方向的分量，则vmin＝vcos 45°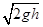＝，方向沿x轴正方向．

本题难度：一般

3、选择题  下列“画阴影”的物体受力分析正确的是 ( ?)

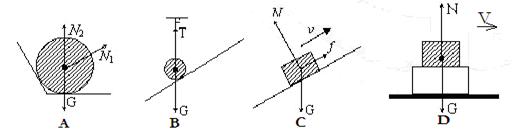
A．两接触面均光滑
B．光滑斜面，挂物体的绳子处于竖直状态
C．物体以初速v依惯性冲上粗糙斜面
D．两物体叠放在水平匀速传送带上一起向右匀速运动

参考答案：BD .

本题解析：光滑的小球静止在墙角，所以小球水平方向受力平衡，故墙对球无支持力（用假设法，如果有该支持力对球而言找不到与之平衡的另一个力故假设不成立，即不存在墙的支持力），故A错误；因为悬绳竖直，光滑小球静止在斜面上，故小球平衡不斜面的支持力，故FN不存在（亦找不到FN的施力物体），故B正确，；
摩擦力与物体间的相对运动方向相反，所以物体受到的摩擦力向下，C错误
两物体一起匀速运动，之间没有相对运动趋势或者相对运动，所以上面的物块只受重力和支持力，D正确，
点评：正确的受力分析是关键，分析受力时不能少力亦不能多力，判断的方法一是找施力物体即分析的每一个力都能找到该力的施力物体，二是满足物体的运动状态即物体在你的受力分析下能保持题设下的运动状态（静止或匀速直线运动等）．

本题难度：简单

4、简答题  如图14所示，一带电量为q=-5×10-3?C，质量为m=0.1kg的小物块处于一倾角为θ=37°的光滑绝缘斜面上，当整个装置处于一水平向左的匀强电场中时，小物块恰处于静止状态．（g取10m/s2）：
（1）求电场强度多大？
（2）若从某时刻开始，电场强度减小为原来的

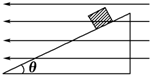
参考答案：（1）

小物块受力如图，则
? 电场力F=mgtanθ
? 又F=qE
? 得到E=mgtanθq=1.5×102N/C
? （2）当电场强度减小为原来的12时，根据动能定理得
? mgLsinθ-q12ELcosθ=12mv2
? 代入解得? v=3m/s
答：（1）电场强度为1.5×10-5N/C．
? （2）若从某时刻开始，电场强度减小为原来的12，物块下滑距离L=1.5m时的速度大小为3m/s．

本题解析：

本题难度：一般

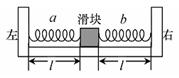
5、选择题  “加速度计”的部分结构简图如图所示，滑块与轻弹簧a、b连接并置于光滑凹槽内，静止时a、b长度均为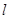；若该装置加速向右运动，a、b长度分别为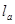、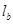，则（?）

A．
B．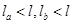
C．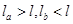
D．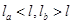

参考答案：D

本题解析：由题意知，静止时，根据平衡条件两弹簧对滑块的弹力等大反向，两弹簧可能同时处于拉伸或压缩状态；若向右加速运动，根据牛顿第二定律可知两弹簧合力向右，若两弹簧时压缩，则a弹簧弹力增大，b弹簧弹力减小，即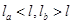；若两弹簧时伸长状态，则a弹簧弹力减小，b弹簧弹力增大，即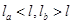，所以D正确；A、B、C错误。

本题难度：一般