1、计算题 (16分)如图所示装置由加速电场、偏转电场和偏转磁场组成。偏转电场处在加有电压的相距为d的两块水平平行放置的导体板之间,匀强磁场水平宽度为l,竖直宽度足够大,处在偏转电场的右边,如图甲所示。大量电子(其重力不计)由静止开始,经加速电场加速后,连续不断地沿平行板的方向从两板正中间射入偏转电场。当两板没有加电压时,这些电子通过两板之间的时间为2t0,当在两板间加上如图乙所示的周期为2t0、幅值恒为U0的电压时,所有电子均能通过电场,穿过磁场,最后打在竖直放置的荧光屏上(已知电子的质量为m、电荷量为e)。求:

(1)如果电子在t=0时刻进入偏转电场,求它离开偏转电场时的侧向位移大小;
(2)通过计算说明,所有通过偏转电场的电子的偏向角(电子离开偏转电场的速度方向与进入电场速度方向的夹角)都相同。
(3)要使电子能垂直打在荧光屏上,匀强磁场的磁感应强度为多少?
参考答案:(1)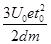 ?(2)见解析?(3)
?(2)见解析?(3)
本题解析:(1)在t=0时刻,电子进入偏转电场,Ox方向(水平向右为正)做匀速直线运动,Oy方向(竖直向上为正)在0-t0时间内受电场力作用做匀加速运动,加速度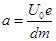 ?(2分)
?(2分)
在t0-2t0时间内做匀速直线运动,速度 ?(1分)
?(1分)
侧向位移 ?(2分)
?(2分)
解得: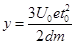 ?(1分)
?(1分)
(2)设电子以初速度v0=vx进入偏转电场,在偏转电场中受电场力作用而加速,不管电子是何时进入偏转电场,在它穿过电场的2t0时间内,其Oy方向的加速度是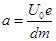 (电压为U0时)或者是0(电压为0时)
(电压为U0时)或者是0(电压为0时)
根据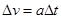 ,可得它在Oy方向上速度增加量都为
,可得它在Oy方向上速度增加量都为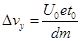 ?(2分)
?(2分)
因此所有电子离开偏转电场时的Oy方向的分速度都相等为 ?(2分)
?(2分)
Ox方向的分速度都为v0=vx,所有电子离开偏转电场的偏向角都相同?(1分)
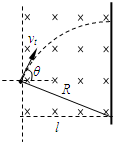
(3)设电子从偏转电场中射出时的偏向角为θ,电子进入匀强磁场后做圆周运动垂直打在荧光屏上,如下图所示,电子在磁场中运动的半径R为: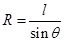 ?(2分)
?(2分)
设电子从偏转电场中出来时的速度为vt,则电子从偏转电场中射出时的偏向角为: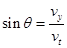 ?(1分)
?(1分)
电子进入磁场后做圆周运动,其半径R为: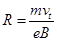 ?(1分)
?(1分)
联立以上各式,解得: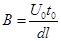 ?(1分)
?(1分)
本题难度:一般
2、简答题 )如图所示,在直角坐标系的第Ⅱ象限和第Ⅳ象限中的直角三角形区域内,分布着磁感应强度均为B=5.0×10-2T的匀强磁场,方向分别垂直纸面向外和向里。质量为m=6.64×10-27kg、电荷量为q=+3.2×10-19C的α粒子(不计α粒子重力),由静止开始经加速电压为U=1 205 V的电场(图中未画出)加速后,从坐标点M(-4,2)处平行于x轴向右运动,并先后通过匀强磁场区域。
?(1)请你求出α粒子在磁场中的运动半径?(2)请你在图中画出α粒子从直线x=-4到直线x=4之间的运动轨迹,并在图中标明轨迹与直线x=4交点的坐标
(3)求出α粒子在两个磁场区域偏转所用的总时间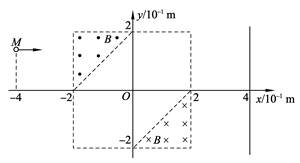
参考答案:(1) (2)图见解析 (3)6.5×10-7 s
(2)图见解析 (3)6.5×10-7 s
本题解析:(1) α粒子在电场中被加速,由动能定理得qU="1/2" mv2(3分)
α粒子在磁场中偏转,则牛顿第二定律得qvB=mv2/r(2分)
联立解得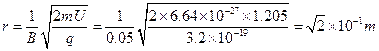 (1分)
(1分)
(2) 能正确作出图象得(6分)

(3) 带电粒子在磁场中的运动周期
T=2πr/v=2πm/qB(2分)
α粒子在两个磁场中偏转的角度均为π/4,在磁场中的运动总时间
t="1/4" T=πm/2qB=(3.14×6.64×10-27)/(2×3.2×10-19×5×10-2)=6.5×10-7 s(3分)
本题难度:一般
3、计算题 (10分)如图,在3、4象限有垂直纸面向外的匀强磁场,在1、2象限有竖直向下的匀强电场。现从y轴上的P点(其坐标为(0,a))水平向右发射一质量为m,电量为q,速度为V0的带电粒子(不计重力).它与+x方向成45°角进入第4象限。
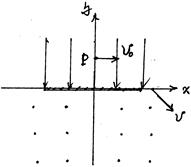
(1)电场强度的大小?
(2)若有一长略大于3a的绝缘弹性板放在x轴上,且中点与坐标原点重合,问磁感应强度多少时,粒子与薄板弹性碰撞后(即碰撞前后水平分速度不变,竖直分速度大小不变,方向相反)可再次从第2象限直接回到P点?
参考答案:
本题解析:(1)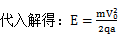 (2)
(2)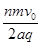 (1)由能量守恒定律可得:
(1)由能量守恒定律可得:
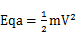 ?
?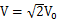
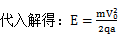
(2)电荷要回到P点,轨迹必须满足对称性,由对称性可得:
电荷的回旋半径r必须满足:
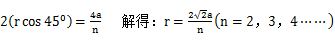
同时为了保证电荷能够与绝缘板碰撞,回旋半径的最小值必须满足:
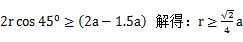
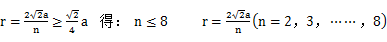
又: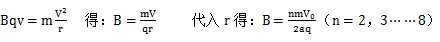
点评:本题难度较大,在电场中应用动能定理不难求得场强大小,但进入磁场后粒子的运动轨迹如何还要判断初速度方向,能够明确回旋半径的最小值是解决本题的关键
本题难度:一般
4、计算题 (17分)如图所示,真空中有以O1为圆心,r为半径的圆形匀强磁场区域,坐标原点O为圆形磁场边界上的一点。磁场的磁感应强度大小为B,方向垂直于纸面向外。x=r的虚线右侧足够大的范围内有方向竖直向下、大小为E的匀强电场。从O点在纸面内向各个不同方向发射速率相同的质子,设质子在磁场中的偏转半径也为r,已知质子的电荷量为e,质量为m。求:
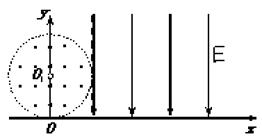
(1)质子射入磁场时的速度大小;
(2)速度方向沿y轴正方向射入磁场的质子到达x轴所需的时间;
(3)速度方向与y轴正方向成37°角且与x轴正方向成127°角射入磁场的质子到达x轴时的位置坐标。(已知sin37°=0.6,cos37°="0.8)"
参考答案:(1)v=eBr/m(2  (3)(
(3)(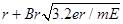 ,0)
,0)
本题解析:(1)设质子射磁场时的速度为v。质子射入磁场后做匀速圆周运动,有evB=mv2/r (2分)
所以v="eBr/m" (1分)
(2)如图,质子沿y轴正方向射入,在磁场中以O2为圆心转过1/4圆弧后从A点垂直于电场方向进入电场。在磁场中的运动周期为T="2πm/(eB)" (1分)

所以质子在磁场中的运动时间? t1="T/4=πm/(2eB)" (1分)
质子进入电场后做类平抛运动,其侧移距离y=at22/2=r(1分)
质子在电场中的加速度a=eE/m(1分)
所以质子在电场中的运动时间t2=  (1分)
(1分)
故质子到达x轴所需的时间t=t1+t2=πm/(2eB)+ ?(1分)
?(1分)
(3)质子射入磁场后,在磁场中以O3为圆心做匀速圆周运动,从P点射出磁场,如图所示,OO1PO3是边长为r的菱形,PO3平行于y轴,质子射出磁场后速度方向与x轴平行。
P点距x轴的距离h=r+rcos53°(3分)

质子垂直于电场方向进入电场做类平抛运动,到达x轴上的Q点。竖直方向的位移h=eEt2/2m (2分)
水平方向的位移s=vt(1分)
解得: ?(1分)
?(1分)
所以Q点的坐标为(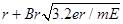 ,0)(1分)
,0)(1分)
本题难度:一般
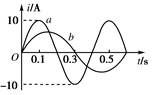
5、选择题 如右图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( ? )
A.线圈先后两次转速之比为3∶2
B.两种情况在0.3 s内通过线圈的磁通量之比为1∶1
C.两种情况在相等时间内产生的焦耳热之比Qa∶Qb=3∶2
D.两种情况在相等时间内产生的焦耳热之比Qa∶Qb=9∶4