1、选择题  如图11所示，在水平地面上方有正交的匀强电场和匀强磁场，匀强电场方向竖直向下，匀强磁场方向水平向里。现将一个带正电的金属小球从M点以初速度v0水平抛出，小球着地时的速度为v1，在空中的飞行时间为t1。若将磁场撤除，其它条件均不变，那么小球着地时的速度为v2，在空中飞行的时间为t2。小球所受空气阻力可忽略不计，则关于v1和v2、t1和t2的大小比较，以下判断正确的是（?）

A．v1=v2
B．v1＜v2
C．t1＜t2
D．t1＞t2

参考答案：AD

本题解析：洛伦兹力不做功，所以落地速度大小不变，由于洛伦兹力方向向上，撤去磁场后运动时间变短，D对；

本题难度：一般

2、计算题  如图所示，与水平面成37°的倾斜轨道AC，其延长线在D点与半圆轨道DF相切，全部轨道为绝缘材料制成且位于竖直面内，整个空间存在水平向左的匀强电场，MN的右侧存在垂直于纸面向里的匀强磁场（C点在MN边界上）。一质量为0.4 kg的带电小球沿轨道AC下滑，至C点时速度为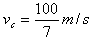，接着沿直线CD运动到D处进入半圆轨道，进入时无动能损失，且恰好能通过F点，在F点速度vF=4 m/s，（不计空气阻力，g=10 m/s2，cos37°=0.8）求：
（1）小球带何种电荷？
（2）小球在半圆轨道部分克服摩擦力所做的功。
（3）小球从F点飞出时磁场同时消失，小球离开F点后的运动轨迹与直线AC（或延长线）的交点为G（G点未标出），求G点到D点的距离。

参考答案：解：（1）正电荷
（2）依题意可知小球在CD间做匀速直线运动
在D点速度为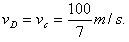
在CD段受重力、电场力、洛伦兹力，且合力为0，设重力与电场力的合力为F，F=qvCB
又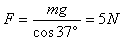
解得：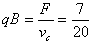
在F点处由牛顿第二定律可得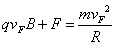
把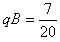代入得，R=1 m
小球在DF段克服摩擦力做功W，由动能定律可得：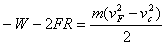
W=27.6 J
（3）小球离开F点后做类平抛运动，其加速度为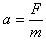
由，得
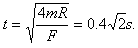
交点G与D点的距离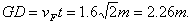

本题解析：

本题难度：困难

3、选择题  在赤道处，将一小球向东水平抛出，落地点为a；给小球带上电荷后，仍以原来的速度抛出，考虑地磁场的影响，下列说法正确的是

[? ]

参考答案：D

本题解析：

本题难度：一般

4、计算题  （12分）如右上图，在xOy平面第一象限整个区域分布一匀强电场，电场方向平行y轴向下．在第四象限内存在一有界匀强磁场，左边界为y轴，右边界为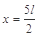的直线，磁场方向垂直纸面向外．一质量为m、带电荷量为+q的粒子从y轴上P点以初速度v0垂直y轴射人匀强电场，在电场力作用下从x轴上Q点以与x轴正方向成450角进入匀强磁场．已知OQ=l，不计粒子重力．求：
（１）粒子到达Q点的速度vQ为多大？
（２）P点的纵坐标是多少？
（３）若该粒子在磁场中运动时刚好不会穿过ｙ轴，求磁感应强度B的大小．

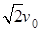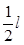参考答案：（1）（2）（3）

本题解析：（1）Q点速度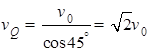
（2）设粒子在电场中运动时间为t，有：
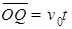?①②
且P点有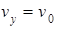③，联解①②③得:?

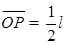（3） 设此时的轨迹半径为r，由几何关系有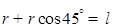：④
粒子在磁场中的速度：? ⑤
根据向心力公式得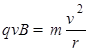： ⑥
联解④⑤⑥得：

本题难度：一般

5、计算题  如图所示，坐标平面的第I象限内存在大小为E、方向水平向左的匀强电场，足够长的挡板MN垂直x轴放置且距离点O为d．第Ⅱ象 限内存在垂直于纸面向里的匀强磁场．磁感应强 度为B。一质量为m，带电量为－q的粒子（重力忽略不计）若自距原点O为L的A点以一定的 速度垂直x轴进入磁场，则粒子恰好到达O点而不进入电场。现该粒子仍从A点进入磁场但初速 度大小为原来的4倍为使粒子进人电场后能垂直到达挡板MN上，求

（1）粒子第一次从A点进入磁场时，速度的大小：
（2）粒子第二次从A点进入磁场时，速度方向与x轴正向间的夹角大小
（3）粒子打到挡板上时的速度大小。

参考答案：（1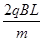）；（2）30°或150°（3）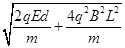

本题解析：
试题分析: （1）粒子自距原点O为L的A点以一定的速度垂直x轴进入磁场，恰好到达O点，轨迹为半圆，则得轨迹半径为r=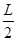，粒子进入匀强磁场中做匀速圆周运动，由洛伦兹力提供向心力，则有：qv0B=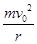，解得v0=；
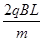（2）设初速度大小为原来的4倍时半径为r1、速度为v1=4v0，由r1=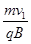，解得r1=2L
为使粒子进入电场后能垂直到达挡板MN上，粒子必须平行于x轴进入电场，设初速度方向与x轴正向间的夹角大小为θ，（如下图）由几何关系知：sinθ=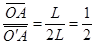得θ=30°或150°

在电场中电场力对粒子做正功，根据动能定理得：qEd=-
解得：v2=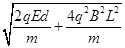

本题难度：一般