1、填空题 两个小球固定在一根长为来源:91考试 网L的杆的两端,绕杆上的固定点O做匀速圆周运动,如图,当小球1 的速度为v1时,小球2 的速度为v2,则转轴到球1的距离是?
参考答案: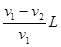
本题解析:两球具有相同的角速度,所以 ,计算可得转轴到球1的距离
,计算可得转轴到球1的距离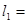
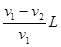
故答案为: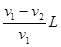
本题难度:简单
2、填空题 A、B两质点分别做匀速圆周运动,若在相等时间内它们通过的弧长之比为SA:SB=1:2,而通过的圆心角之比φA:φB=2:1,则它们的周期之比_______________,线速度之比=_______________,角速度之比_______________。?
参考答案:1:2? 1:2? 2:1
本题解析:由线速度公式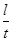 可知线速度之比为1:2,由角速度公式
可知线速度之比为1:2,由角速度公式 可知角速度之比为1:2,由周期公式
可知角速度之比为1:2,由周期公式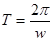 可知周期之比为2:1
可知周期之比为2:1
本题难度:简单
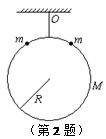
3、选择题 如图2所示,有一质量为M的大圆环,半径为R,被一轻杆固定后悬挂在O点,有两个质量为m的小环(可视为质点),同时从大环两侧的对称位置由静止滑下。两小环同时滑到大环底部时,速度都为v,则此时大环对轻杆的拉力大小为(?)
A.(2m+2M)g
B.Mg-2mv2/R
C.2m(g+v2/R)+Mg
D.2m(v2/R-g)+Mg
参考答案:C
本题解析:每个小环滑到大环底部时,有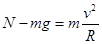 ,则大环的作用力为:
,则大环的作用力为: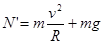 ,方向向下,则两小环同时滑到大环底部时,大环对轻杆的拉力为Mg+2m(g+v2/R),C正确。
,方向向下,则两小环同时滑到大环底部时,大环对轻杆的拉力为Mg+2m(g+v2/R),C正确。
本题难度:简单
4、计算题 (19分)如图所示,带正电的绝缘小滑块A,被长R=0.4m的绝缘细绳竖直悬挂,悬点O距水平地面的高度为3R;小滑块B不带电.位于O点正下方的地面上。长L=2R的绝缘水平传送带上表面距地面的高度h=2R,其左端与O点在同一竖直线上,右端的右侧空间有方向竖直向下的匀强电场。在O点与传送带之间有位置可调的固定钉子(图中未画出),当把A拉到水平位置由静止释放后,因钉子阻挡,细绳总会断裂,使得A能滑上传送带继续运动,若传送带逆时针匀速转动,A刚好能运动到传送带的右端。已知绝缘细绳能承受的最大拉力是A重力的5倍,A所受电场力大小与重力相等,重力加速度g=10m/s2,A.B均可视为质点,皮带传动轮半径很小,A不会因绳断裂而损失能量、也不会因摩擦而损失电荷量。试求:
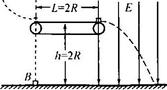
(1)钉子距O点的距离的范围。
(2)若传送带以速度v0=5m/s顺时针匀速转动,在A刚滑到传送带上时,B从静止开始向右做匀加速直线运动,当A刚落地时,B恰与A相碰。试求B做匀加速运动的加速度大小(结果可用根式表示)
参考答案:(1) 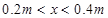 (2)
(2) 
本题解析:
(1)在A运动到最低点的过程中,由机械能守恒定律,有: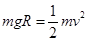 (2分)
(2分)
得: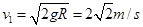 (1分)
(1分)
A到最低点,绳子被挡住时,有: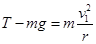 (1分)
(1分)
当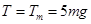 时,解得
时,解得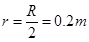 (1分)
(1分)
故钉子距离O点的距离范围是: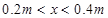 . (1分)
. (1分)
(2)在A运动到传送带右端的过程中,因钉子挡绳不损失能量,有动能定理有:
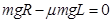 (2分)
(2分)
解得: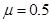 (1分)
(1分)
因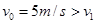 ,所以A在传送带上将做加速运动,假设A一直加速,到右端的速度为
,所以A在传送带上将做加速运动,假设A一直加速,到右端的速度为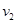 ,
,
由动能定理有: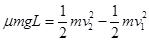 (1分)
(1分)
解得: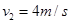 (1分)
(1分)
因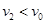 ,假设成立,A一直做加速运动;因皮带传动轮半径很小,故A在传送带右端将以
,假设成立,A一直做加速运动;因皮带传动轮半径很小,故A在传送带右端将以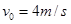 的初速度做类平抛运动 (1分)
的初速度做类平抛运动 (1分)
对A:设在传送带上运动的时间为t1,类平抛运动的时间为t2,
有运动学规律传送带上: (1分)
(1分)
类平抛运动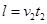 (1分)
(1分)
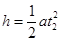 (1分)
(1分)
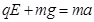 (1分)
(1分)
解得: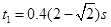 ,
,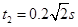 ,
,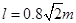
对B:设匀加速过程的加速度大小为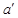 ,则有:
,则有:
位移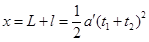 (1分)
(1分)
解得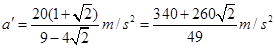 (2分)
(2分)
考点:本题考查了平抛运动规律、动能定理和机械能守恒定律的应用
本题难度:困难
5、选择题 如图所示的皮带传动装置,主动轮O1上两轮的半径分别为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带不打滑,则下列选项正确的是:(?)

A.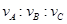 =3:1:3? B.
=3:1:3? B.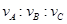 =3:1:1?
=3:1:1?
C.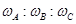 =3:3:1? D.
=3:3:1? D.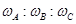 =1:3:3
=1:3:3
参考答案:B
本题解析:设B的角速度为w,则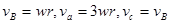 ,由此可知B对;
,由此可知B对;
本题难度:简单