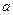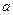1、计算题  所示，“目”字形轨道的每一短边的长度都等于，只有四根平行的短边有电阻，阻值都是r，不计其它各边电阻。使导轨平面与水平面成夹角固定放置，如图乙所示。一根质量为m的条形磁铁，其横截面是边长为的正方形，磁铁与导轨间的动摩擦因数为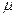，磁铁与导轨间绝缘。假定导轨区域内的磁场全部集中在磁铁的端面，并可视为匀强磁场，磁感应强度为B，方向垂直导轨平面。开始时磁铁端面恰好与正方形3重合，现使其以某一初速度下滑，磁铁恰能匀速滑过正方形2，直至磁铁端面恰好与正方形l重合。已知重力加速度为g。求：
（1）上述过程中磁铁运动经历的时间；
（2）上述过程中所有电阻消耗的电能。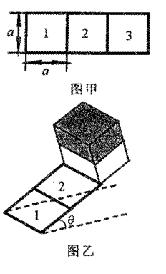

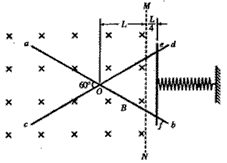
2、计算题  如图所示，“ ×”型光滑金属导轨abcd固定在绝缘水平面上，ab和cd足够长，∠aOc =60°，虚线MN与∠bOd的平分线垂直，O点到MN的距离为L。MN左侧是磁感应强度大小为B、方向竖直向下的匀强磁场。一轻弹簧右端固定，其轴线与∠bOd的平分线重合，自然伸长时左端恰在O点。一质量为m的导体棒ef平行于MN置于导轨上，导体棒与导轨接触良好。某时刻使导体棒从MN的右侧处由静止开始释放，导体棒在压缩弹簧的作用下向左运动，当导体棒运动到O点时弹簧与导体棒分离，导体棒由MN运动到O点的过程中做匀速直线运动，导体棒始终与MN平行。已知导体棒与弹簧彼此绝缘，导体棒和导轨单位长度的电阻均为r0，弹簧被压缩后所获得的弹性势能可用公式Ep=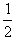kx2计算，k为弹簧的劲度系数，x为弹簧的形变量。
（1）求导体棒在磁场中做匀速直线运动过程中的感应电流的大小，并判定大小变化特点；
（2）求弹簧的劲度系数k和导体棒在磁场中做匀速直线运动时速度v0的大小；
（3）求导体棒最终静止时的位置距O点的距离。

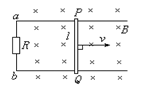
3、选择题  如图所示，在磁感应强度B=0.5T的匀强磁场中，让导体PQ在  U形导轨上以v=10m/s向右匀速滑动，两导轨间距离l=0.8m，则产生的感应电动势的大小和PQ中的电流方向分别是（    ）

A  4V，由P向Q      B  0.4V，由Q向P
C  4V，由Q向P      D  0.4V，由P向Q

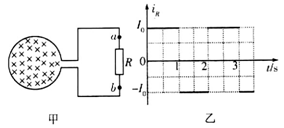
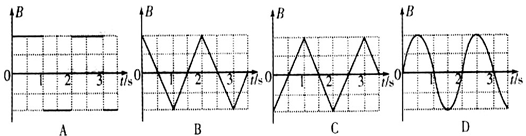
4、选择题  如图甲所示，圆形导线框与电阻R串联，框内有变化的磁场．取由a经R流向b为感应电流的正方向，测得随时间t变化的图象如图乙所示．取垂直纸面向里为磁场的正方向，则描述磁感应强度B随时间t变化的图象正确的是

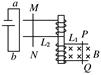
5、选择题  如图所示，水平放置的两条光滑轨道上有可自由移动的金属棒PQ、MN，MN的左边有一闭合电路，当PQ在外力的作用下运动时，MN向右运动．则PQ所做的运动可能是(  )

A．向右加速运动
B．向左加速运动
C．向右减速运动
D．向左减速运动