1、计算题 质量为m的小物块,用轻弹簧固定在斜面体上,斜面的倾角为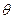 ,轻弹簧的劲度系数为k,如图所示.整个装置放在电梯内.
,轻弹簧的劲度系数为k,如图所示.整个装置放在电梯内.
(1)若斜面光滑,电梯静止时弹簧的伸长量为x.如果电梯竖直向上做匀加速直线运动,弹簧的伸长量为2 x.求电梯竖直向上加速运动时的加速度.
(2)若斜面不光滑,斜面与物块之间的动摩擦因数为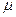 ,弹簧的伸长量也为2 x,求此时电梯上升加速度的最大值.(设最大静摩擦力与滑动摩擦力大小相等)
,弹簧的伸长量也为2 x,求此时电梯上升加速度的最大值.(设最大静摩擦力与滑动摩擦力大小相等)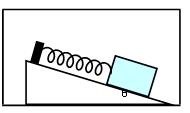
参考答案:(1)小物块的受力情况如图(1)所示。
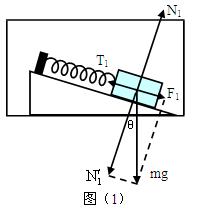
由胡克定律得: ?①?(1分)
?①?(1分)
重力沿斜面的下滑力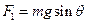 ?②?(1分)
?②?(1分)
沿斜面方向有: ?③?(2分)
?③?(2分)
解得: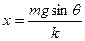 ?④?(2分)
?④?(2分)
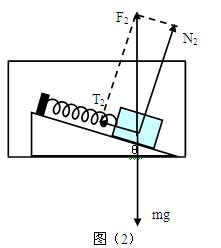
若电梯竖直向上做匀加速直线运动,小物块受力情况如图(2)所示,受重力 mg,斜面的支持力N2以及弹簧的弹力T2.其中F2为N2与T2合力.
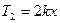 ?⑤?(1分)
?⑤?(1分)
 ?⑥?(1分)
?⑥?(1分)
由牛顿第二定律得:  ?⑦?(2分)?
?⑦?(2分)?
联立④⑤⑥⑦解得: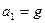 ?(1分)
?(1分)
(结果为 不扣分)(其它方法参照给分)
不扣分)(其它方法参照给分)
(2)若斜面不光滑 ,小物块的受力分析如图(3)所示,受重力mg,斜面的支持力N3和摩擦力f,弹簧的弹力,大小仍为T2.
,小物块的受力分析如图(3)所示,受重力mg,斜面的支持力N3和摩擦力f,弹簧的弹力,大小仍为T2.
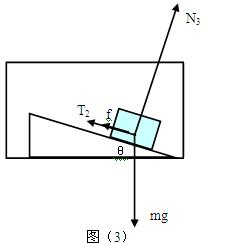
水平方向上: ?⑧ (1分)
?⑧ (1分)
竖直方向上: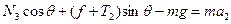 ?⑨(1分)
?⑨(1分)
加速度最大时,摩擦力为最大静摩擦力,即 ?⑩?
?⑩?
联立④⑤⑧⑨⑩解得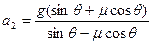 ?(1分)
?(1分)
本题解析:略
本题难度:简单
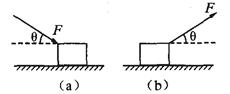
2、计算题 如图所示,一个人用与水平方向成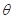 = 300角的斜向下的推力F推一个质量为20 kg的箱子匀速前进,如图(a)所示,箱子与水平地面间的动摩擦因数为
= 300角的斜向下的推力F推一个质量为20 kg的箱子匀速前进,如图(a)所示,箱子与水平地面间的动摩擦因数为 =0.40.
=0.40.
求:
(1)推力F的大小;
(2)若该人不改变力F的大小,只把力的方向变为与水平方向成300角斜向上去拉这个静止的箱子,如图(b)所示,拉力作用2.0 s后撤去,箱子最多还能运动多长距离?(g取10 m/s2).
参考答案:(1) 120N?(2)13.5m
本题解析:(1)在图(a)情况下,箱子匀速前进,对箱子有
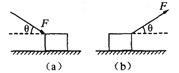

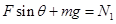
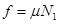
由以上三式得F=120N.
(2)在图(b)情况下,物体先以加速度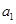 做匀加速运动,然后以加速度
做匀加速运动,然后以加速度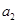 做匀减速运动直到停止.对物体有
做匀减速运动直到停止.对物体有
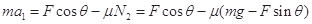
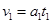
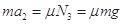
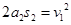
解得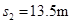 .
.
点评:关键是物体的受力情况分析和运动情况分析,分清物体的运动过程,采用牛顿运动定律和运动学公式结合求解是基本方法。
本题难度:一般
3、选择题 如图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态。现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2。重力加速度大小为g。则有
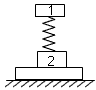
[? ]
A.a1=0,a2=g
B.a1=g,a2=g
C.
D.
参考答案:C
本题解析:
本题难度:一般
4、选择题 如图所示,水平木板上有质量m=1.0kg的物块,受到随时间t变化的水平拉力F作用,用力传感器测出相应时刻物块所受摩擦力Ff的大小.取重力加速度g=10m/s2,下列判断正确的是( )
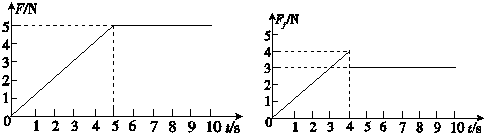
A.4s内拉力对物块做功为零
B.4s末物块所受合力大小为4.0N
C.物块与木板之间的动摩擦因数为0.3
D.6s~9s内物块的加速度大小为2.0m/s2
参考答案:A、在0-4s内,物体所受的摩擦力为静摩擦力,4s末开始运动,故4s内拉力做功为零,故A正确;
B、4s末拉力为4N,摩擦力为4N,合力为零.故B错误.
C、由图可知,滑动摩擦力为3N,则由f=μmg;解得μ=fmg=310=0.3;故C正确;
D、由图可知拉力为5N,摩擦力为3N,则合力F合=F-f=5-3=2N;故加速度为:a=F合m=2.0m/s2;故D正确;
故选:ACD.
本题解析:
本题难度:一般
5、简答题 质量为4kg的物体在一恒定水平外力F作用下,沿水平面作直线运动,其速度与时间关系图象如图所示g=10m/s2,试求:
(1)恒力F的大小;
(2)地面动摩擦因数μ.
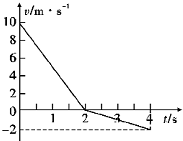
参考答案:由图象可知物体0~2s做匀减速直线运动,设加速度为a1,2~4s做反向匀加速直线运动,设加速度分别为a2.且恒力F与初速度方向相反.
由v-t图象得:a1=0-102=-5m/s2
a2=-1m/s2
由牛顿第二定律得:F-μmg=ma1(3)
F+μmg=ma2(4)
联(3)(4)立解得:F=m(a1+a2)2(5)
μ=(a2-a1)2g(6)
将(1)(2)代入(5)(6)得:F=-12N负号表示力的方向于正方向相反即与初速度方向相反μ=0.2
即力F的大小为12N;摩擦因数为0.2
答:(1)恒力F的大小为12N;(2)动摩擦因数为0.2.
本题解析:
本题难度:一般
As is the workman so is the work. 什么匠人出什么活儿.