1、简答题  
在光滑的水平面上，一个质量较大的物体与一个质量较小的静止物体发生正碰后能否被反弹回来？试加以分析讨论。

参考答案：
质量较大的物体是不会被反弹回来的。

本题解析：
假设质量为M的较大物体，以速度v碰撞质量为m的较小物体后能反弹回来，且其反弹的速度为V"，而m前进的速度为v"，则根据动量守恒定律得
Mv=mv"-MV"?①

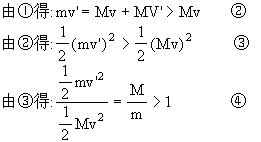
由④得出碰撞后质量较小的物体获得的动能大于质量较大物体原有的动能，这是违背能量守恒定律的，这说明前面假设是错误的，所以质量较大的物体是不会被反弹回来的。

本题难度：简单

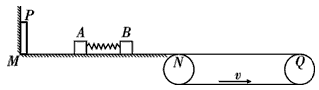
2、计算题  如图所示，光滑水平面MN的左端M处有一弹射装置P，右端N处与水平传送带理想连接。传送带水平部分长L＝8m，并以恒定速度v＝3m/s沿图示箭头方向移动。质量均为m＝1kg、静止于MN上的物块A、B（视为质点）之间压缩一轻弹簧，贮有弹性势能EP＝16J。若A、B与传送带间的动摩擦因数μ＝0.2，则解除弹簧压缩，弹开物块A、B后，求：
（1）物块B在传送带上向右滑行的最远距离L1；
（2）物块B返回到水平面MN时的速度vB′；
（3）若物块B返回水平面MN后，与被弹射装置P弹回的物块A在水平面MN上弹性碰撞（碰撞过程无动能损失，碰撞时间极短），使物块B从传送带水平部分的右端Q滑出，则弹射装置P必须给物块A至少做多少功？

参考答案：解：（1）解除锁定后弹簧恢复原长时，A、B的速度大小分别为vA、vB，
由系统机械能守恒、动量守恒mBvB＝mAvA?

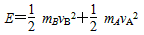
联立解得vA＝vB＝4m/s
设B沿传送带向右滑行的最远距离为L1，由功能关系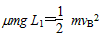
解得L1＝4m
（2）因为v＝4m/s＞3m/s，所以B返回时先加速再随传送带一起运动，
B返回到水平面MN时的速度vB′＝3m/s
（3）以A为研究对象，设碰后A、B的速度分别为vA′、vB′′，
由动能定理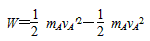
B能从Q端滑出一定有?
A与B质量相等，完全弹性碰撞后速度互换，则A的速度vA′＝vB′′
联立解得 W≥8J。

本题解析：

本题难度：困难

3、计算题  如图所示，甲车质量为m1=2kg，静止在光滑水平面上，上表面光滑，右端放一个质量为m0=1kg的小物体，可视为质点；乙车质量为m2=4kg，以v0=5m/s的速度向左运动，与甲车碰撞，碰撞时间极短，且碰后甲车获得v1=4m/s的速度，物体滑到乙车上；若乙车足够长，上表面与物体的动摩擦因数为μ=0.2，求：

（1）碰撞后乙车的速度v2？
（2）物体在乙车上滑过的痕迹长度l等于多少？
（3）从碰撞开始经过t=2s时，物体距甲车右端多远？

参考答案：1）略
2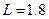）m?
3）4.64m

本题解析：解：（1）甲、乙相碰瞬间，小物体速度不变，甲、乙为系统动量守恒，以向左为正向：
?
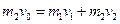得： m/s，乙碰后向左运动?（4分）
（2）小物块滑到乙车上，与乙车相对静止，令共同速度为u，

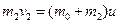
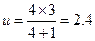m/s，
正号说明u与正方向相同，最终共同向左运动。?（3分）
据能量转化与守恒有：

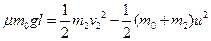
代入数据联解可得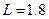：m?（3分）
（3）小物块在B上匀加速到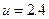m/s时，令所用时间为t1，有：
s??（2分）
在此时间内小物块所运动位移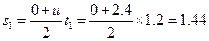：m
余下时间内小物块所运动位移：m
物体距甲车右端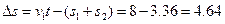：m?（4分）

本题难度：简单

4、选择题  如图4所示，质量为M的物体P静止在光滑的水平面上，有另一质量为m(M＞m)的物体Q以速度v0正对P滑行，则它们碰后（水平面足够大）（?）

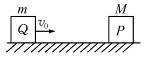
图4
A．Q物体一定被弹回，因为M＞m
B．Q物体可能继续向前
C．Q物体的速度可能为零
D．若相碰后两物体分离，则过一段时间可能再相碰

参考答案：BC

本题解析：由题意知m＜M,两物体如果为完全非弹性碰撞，则P、Q黏在一起共同运动，所以选项A不对.如果为弹性碰撞，则一定被弹回；当为非完全弹性碰撞时，Q的速度随着损失能量的增加介于被弹回和一起向前运动之间，因而可能为零，故C对.再由运动学知识知，分离后不会再碰，故D不对.

本题难度：简单

5、选择题  在光滑的水平面上有质量相等的A、B两球，其动量分别为10kg·m/s与2kg·m/s，方向均向东，且定为正方向，A球在B球后，当A球追上B球发生正碰，则相碰以后，A、B两球的动量可能分别为
A．6kg·m/s，6kg·m/s        B．-4kg·m/s，16kg·m/s
C．6kg·m/s，12kg·m/s       D．3 kg·m/s，9kg·m/s

参考答案：AD

本题解析：碰撞前后应满足动量守恒，C错。碰前两球动能，，碰撞前后能量不增加，只有D选项符合题意。
考点：本题考查了动量守恒定律。

本题难度：一般