1、选择题  一个质子以1.0×107m/s的速度撞入一个静止的铝原子核后被俘获，铝原子核变为硅原子核，已知铝核的质量是质子的27倍，硅核的质量是质子的28倍，则下列判断中正确的是
[? ]
A.核反应方程为
B.核反应方程为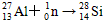
C.硅原子核速度的数量级为107m/s，方向跟质子的初速度方向一致
D.硅原子核速度的数量级为105m/s，方向跟质子的初速度方向一致

参考答案：AD

本题解析：

本题难度：一般

2、计算题  【选修3-5选做题】
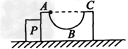
如图所示，质量为m1=3kg的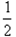光滑圆弧形轨道ABC与一质量为m2=1 kg的物块P紧靠着（不粘连）静置于光滑水平面上，B为半圆轨道的最低点，AC为轨道的水平直径，轨道半径R=0.3 m。一质量为m3 =2 kg的小球（可视为质点）从圆弧轨道的A处由静止释放，g取10m/s2，求：
(1)小球第一次滑到B点时的速度v1；
(2)小球第一次经过B点后，相对B能上升的最大高度h。

参考答案：解：（1）设小球第一次滑到B点时的速度为v1，轨道和P的速度为v2，取水平向左为正方向
由水平方向动量守恒有(m1+m2)v2+m3v1=0
根据系统机械能守恒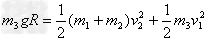
联立解得v1=-2 m/s，方向向右；v2=1m/s，方向向左
（2）小球经过B点后，物块P与轨道分离，小球与轨道水平方向动量守恒，且小球上升到最高点时与轨道共速，设为v
m1v2+m3v1=(m1+m3)v
解得v=-0.2 m/s，方向向右
由机械能守恒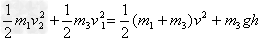
解得h=0.27 m

本题解析：

本题难度：一般

3、简答题  如图所示，甲、乙两光滑圆轨道放置在同一竖直平面内，甲轨道半径是R且为乙轨道半径的2倍，两轨道之间由一光滑水平轨道CD相连，在水平轨道CD上有一轻弹簧被a、b两个小球夹住，但不拴接．如果a、b两个小球的质量均为m，同时释放两小球，且要求a、b都能通过各自的最高点，则弹簧在释放前至少具有多大的弹性势能？

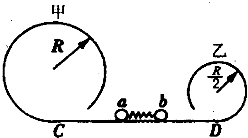
参考答案：当a球恰能通过最高点时，b球一定通过最高点，此时弹簧在释放前具有的弹性势能最小，设a球到达圆轨道最高点的速度为va，对于a球有：
mag=mav2aR…①
设a球被弹簧弹开瞬间的速度为v"a，对于a球由机械能守恒定律可得：12mav′2a=12mav2a+mag2R… ②
设b球被弹簧弹开瞬间的速度为v"b，由于a、b两球被弹开时系统动量守恒：mav"a=mbv"b …③
①②③可得：v′a=v′b=

本题解析：

本题难度：一般

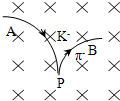
4、选择题  Kˉ介子衰变的方程为K-→π-+π0，如图所示，其中Kˉ介子和πˉ介子带负的基元电荷，π0介子不带电．一个Kˉ介子沿垂直于磁场的方向射入匀强磁场中，其轨迹为圆弧AP，衰变后产生的πˉ介子的轨迹为圆弧PB，两轨迹在P点相切，它们的半径RKˉ与Rπ-之比为2：1．π0介子的轨迹未画出．由此可知πˉ介子的动量大小与π0介子的动量大小之比为（　　）
A．1：1
B．1：2
C．1：3
D．1：6