1、填空题  某一行星有一质量为m的卫星，以半径r，周期T做匀速圆周运动，行星的质量                       

参考答案：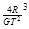

本题解析：
考点：万有引力定律及其应用．
分析：由万有引力提供向心力，可以列式求解；
解：设行星的质量为M，由行星对卫星的万有引力提供向心力得
G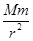=r=ma
解之得
M=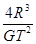
故答案为：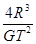

本题难度：一般

2、选择题  关于匀速圆周运动，下列认识正确的是（　　）
A．匀速圆周运动是匀速运动
B．匀速圆周运动是变速运动
C．匀速圆周运动的线速度不变
D．匀速圆周运动的周期不变

参考答案：物体沿着圆周运动，再任意相等时间内通过的弧长相等的运动叫做匀速圆周运动；
A、匀速圆周运动是曲线运动，速度方向是切线方向，时刻改变，故线速度是变化的，所以是变速运动，故AC错误，B正确；
D、周期是转动一圈的时间，是不变的，故D正确；
故选BD．

本题解析：

本题难度：一般

3、计算题  (9分) 如图所示，水平轨道AB与竖直半圆形光滑轨道在B点平滑连接，半圆形轨道半径R=2.5m，质量m=0.1kg的小滑块（可视为质点）以一定的速度从水平轨道进入半圆形轨道，沿轨道运动恰好能到最高点C，且从C点水平飞出后恰好落在A点，重力加速度g=10m/s2，试分析求解：

(1)滑块通过C点时的速度大小；
(2)AB间的距离x。

参考答案：（1）5m/s   （2）5m

本题解析：（1）由题意知，在C点：（2分）
解得：（4分）
（2）从C到A，小滑块做平抛运动，根据平抛运动的规律：
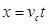 （2分）
   （2分）
解得：x=5m（1分）
考点：本题考查平抛运动、圆周运动

本题难度：一般

4、选择题  如图所示，用细线悬着一个小球在空中沿水平面做匀速圆周运动，小球受到的作用力是：

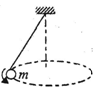
A．重力和细线的拉力
B．重力、细线的拉力、离心力
C．重力、细线的拉力、向心力
D．重力、细线的拉力、向心力、离心力

参考答案：A

本题解析：本题考查受力分析。对小球受力分析，受重力和细线的拉力，合力提供向心力，选A。

本题难度：一般

5、计算题  如图，质量为0.5kg的小杯里盛有1kg的水，用绳子系住小杯在竖直平面内做“水流星”表演，转动半径为1m，小杯通过最低点的速度为8m/s，g取10m/s2，求：

（1）小杯在最高点时，绳的拉力；
（2）小杯在最高点时水对小杯底的压力；
（3）为使小杯过最高点时水不流出，在最低点时的最小速率。

参考答案：（1）21N，方向竖直向下（2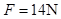）方向竖直向上（3）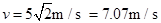

本题解析：（1）从最低点到最高点，应用动能定理，得
?（2分）
在最高点： ?（1分）
得?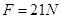
绳的拉力大小为21N，方向竖直向下?（1分）
（2）在最高点对水得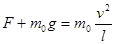：?（2分）
得?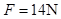?由牛顿第三定律得，水对杯底的压力大小为14N，
方向竖直向上。?（2分）
（3）杯子和水整体在最高点的最小速度为：
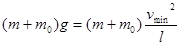?（2分）
从最高点到最低点应用动能定理：
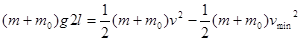?（1分）
得最低点的最小速度为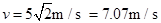：?（1分）
本题考查的是竖直平面内圆周运动中的临界问题。竖直平面内的圆周运动一般是变速圆周运动,对这类问题现行教材和高考只要求讨论最高点和最低点的情况.注意绳约束和杆约束的区别,弄清不同情况下的临界速度,是分析解决这类问题的关键.

本题难度：一般