1、计算题  如图所示，可看成质点的A、B两个小球，质量分别为m和2m，用细绳连接后跨在固定的光滑圆柱体上，圆柱的半径为R.先使小球B处于与圆柱中心等高，则小球A张紧细绳后刚好接触地面，再将小球B无初速释放，当B球着地后，A球能继续上升的最大高度是?.

参考答案：R/3

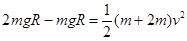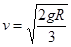本题解析：当B球触地时，设两球的速度均为v，则根据机械能守恒定律得，解得,此后A球做竖直上抛运动，还能上升的最大高度为.

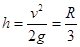本题难度：一般

2、计算题  如图所示，一不可伸长的轻质细绳，绳长为L一端固定于O点，另一端系一质量为m的小球，小球绕O点在竖直平面内做圆周运动（不计空气助力），小球通过最低点时的速度为v。

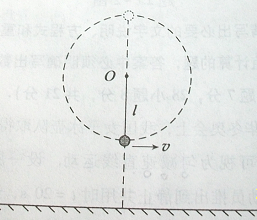
（1）求小球通过最低点时，绳对小球拉力F的大小；
（2）若小球运动到最低点或最高点时，绳突然断开，两种情况下小球从抛出到落地水平位移大小相等，求O点距地面的高度h;
（3）在(2)中所述情况下试证明O点距离地面高度h与绳长l之间应满足

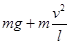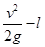参考答案：（1）（2）（3）由于?∴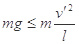
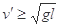
由机械能守恒定律?得小球运动到最低点时速度有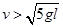，由（2）中结果得。

本题解析：（1）根据向心力公式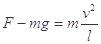有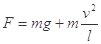
（2）小球运动到最低点，绳突然断开后小球做平抛运动时间为，则
，?
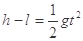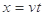
设运动到最高点速度为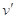，由机械能守恒定律得
?
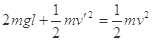小球运动到最高点绳断开后平抛运动时间为，则
，?
又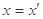
联立上述各式解得
（3）小球运动到最高点时向心力最小值为，则有
?∴
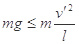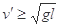
那么由机械能守恒定律??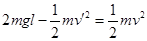
小球运动到最低点时速度有?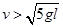
故由（2）问结果，得。
点评：解析此类问题的关键点是分析小球通过最高点和最低点时的受力情况，根据机械能守恒可求得两个特殊位置的速度，抓住小球恰好通过最高点的条件是重力等于此时的向心力。

本题难度：一般

3、填空题  如图所示，在长度一定的细线下方系一小球，线的另一端固定，使悬线与竖直方向成不同偏角θ（0°＜θ≤90°）时无速释放。则小球摆回到最低点P时，细线所受力的大小范围是____________。

参考答案：Mg＜F≤3Mg

本题解析：

本题难度：一般

4、计算题  (12分)两块质量都是m的木块A和B在光滑水平面上均以速度v0/2向左匀速运动，中间用一根劲度系数为k的轻弹簧连接着，如图所示。现从水平方向迎面射来一颗子弹，质量为m/4，速度为v0，子弹射入木块A并留在其中。求：

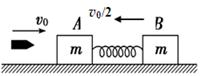
(1)在子弹击中木块后的瞬间木块A、B的速度vA和vB的大小。
(2)在子弹击中木块后的运动过程中弹簧的最大弹性势能。?

参考答案：vB＝v0/2? vA＝v0/5?mv02

本题解析：(1)在子弹打入木块A的瞬间，由于相互作用时间极短，弹簧来不及发生形变，A、B都不受弹力的作用，故vB＝v0/2 ；?（2分）
由于此时A不受弹力，木块A和子弹构成的系统在这极短过程中不受外力作用，系统动量守恒：
mv0/2 — mv0/4 ＝ (m/4＋m) vA，（2分）
解得vA＝v0/5?（2分）
（2）由于木块A、木块B运动方向相同且vA＜vB，故弹簧开始被压缩，分别给A、B木块施以弹力，使得木块A加速、B变减速运动，弹簧不断被压缩，弹性势能增大，直到二者速度相等时弹簧弹性势能最大，在弹簧压缩过程木块A(包括子弹)、B与弹簧构成的系统动量守恒，机械能守恒。
设弹簧压缩量最大时共同速度为v，弹簧的最大弹性势能为Epm，有
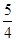?mvA? +? mvB ＝ (5m/4＋m)v?（2分）
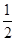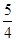?·mvA2?+ 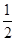?mvB2 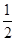＝ ?(5m/4＋m)v2 ＋ Epm ?（2分）
联立解得： v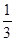＝v0，? Epm＝mv02?（2分）

本题难度：一般

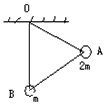
5、选择题  如图所示长度相等的三根轻质竿构成一个正三角形支架，在A处固定一质量为2m的小球，B处固定一 质量为m的小球，支架悬挂于O点，可绕O点并与支架所在平面相垂直的固定轴转动，开始时OB与地面相垂直，放手后开始运动，不计任何阻力，下列说法正确的是

[? ]
A．A球到达最低点时速度为零
B．A球机械能减少量等于B球机械能增加量
C．B球向左摆动所达到的最高点位置应高于A球开始时的高度
D．当支架从左向右回摆时，A球一定能回到原来的高度

参考答案：BCD

本题解析：

本题难度：一般