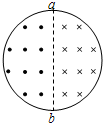
1、简答题  一个负离子，质量为m，电量大小为q，以速率V垂直于屏S经过小孔O射入存在着匀强磁场的真空室中(如图11)。磁感应强度B的方向与离子的运动方向垂直，并垂直于图1中纸面向里。

(1)求离子进入磁场后到达屏S上时的位置与O点的距离。
(2)如果离子进入磁场后经过时间t到达位置P，证明:直线O与离子入射方向之间的夹角θ跟t的关系是。

参考答案：(1)

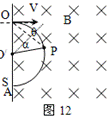
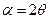(2)当离子到位置P时，圆心角(见图12)：因为，所以。

本题解析：(1)离子的初速度与匀强磁场的方向垂直，在洛仑兹力作用下，做匀速圆周运动。设圆半径为r，则据牛顿第二定律可得：

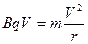?，解得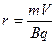
如图12所示，离了回到屏S上的位置A与O点的距离为：AO=2r
所以
(2)当离子到位置P时，圆心角(见图12)：

因为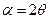，所以。

本题难度：简单

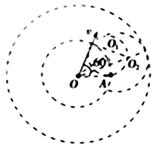
2、计算题  如图所示，两个同心圆，半径分别为r和2r，在两圆之间的环形区域内存在垂直纸面向里的匀强磁场，磁感应强度为B.圆心O处有一放射源，放出粒子的质量为m，带电荷量为q，假设粒子速度方向都和纸面平行, 不计粒子重力。

（1）图中箭头表示某一粒子初速度的方向，OA与初速度方向夹角为60°，要想使该粒子经过磁场第一次通过A点，则初速度的大小是多少？
（2）要使粒子不穿出环形区域，则粒子的初速度不能超过多少？

参考答案：（1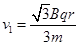）（2）

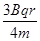
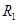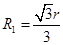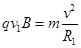本题解析：如图所示，设粒子在磁场中的轨道半径为，则由几何关系可得：，又，联立解得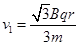

（2）设粒子轨迹与磁场外界相切时，粒子在磁场中的轨道半径为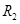，则由几何关系有：

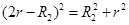
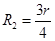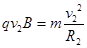可得：，又，可得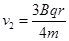
故要使粒子不穿出环形区域，粒子的初速度不能超过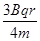
考点：带电粒子在匀强磁场中的运动.

本题难度：一般

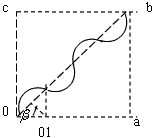
3、计算题  如图所示的正方形平面oabc内，存在着垂直于该平面向外的匀强磁场，磁感应强度大小为B，已知正方形边长为L，一质量为m，带电量为+q的粒子（不计重力）在t=0时刻平行于oc边从o点射入磁场中。
（1）若带电粒子从a点射出磁场，求带电粒子在磁场中运动的时间以及初速度的大小；
（2）若磁场的磁感应强度按如图所示的规律变化，规定磁场向外的方向为正方向，磁感应强度的大小为B0，则要使带电粒子能从oa边界射出磁场，磁感应强度B的变化周期T的最小值应为多少？
（3）若所加磁场与第（2）问中相同，则要使粒子从b点沿ab方向射出磁场，满足这一条件的磁感应强度的变化周期T及粒子射入磁场时的速度V0应为多少？（不考虑磁场变化产生的电场）

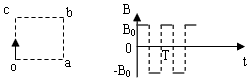
参考答案：解：（1）若带电粒子从a点射出磁场，则其做圆周运动的半径为r=L/2
所需时间为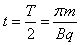
设粒子初速度的大小为v0，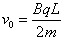
（2）若粒子从oa边射出，则其轨迹如图所示

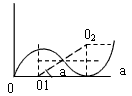
有，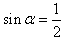
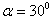
在磁场变化的半个周期内，粒子在磁场中旋转150°，其运动的时间为，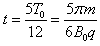
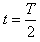
故磁场变化的最小周期为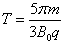
（3）要使粒子从b点沿ab方向射出磁场，其轨迹如图所示

在磁场变化的半个周期中内，粒子在磁场中旋转的角度为2β，，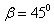
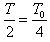
所以磁场变化的周期为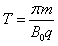
r=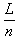（n=2，4，6 …. ），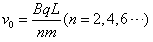

本题解析：

本题难度：困难

4、选择题  如图，在圆形空间区域内存在关于ab直径对称、方向相反的两匀强磁场，两磁场的磁感应强度大小相等，一金属导线制作的圆环刚好与磁场边界重合，下列说法中正确的是（　　）
A．若使圆环向右平动，感应电流先沿逆时针方向后沿顺时针方向
B．若使圆环竖直向上平动，感应电流方向始终沿逆时针
C．若圆环以a、b为轴转动，在0-90°内，由右手定则知a点的电势高于b点的电势
D．若圆环以a、b为轴转动，始终有b点的电势高于a点的电势