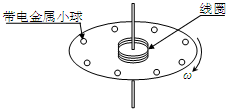
1、简答题 如图所示,一水平放置的平行导体框架宽度L=0.5m,接有电阻R=0.20Ω,磁感应强度B=0.40T的匀强磁场垂直导轨平面方向向下,仅有一导体棒ab跨放在框架上,并能无摩擦地沿框架滑动,框架及导体ab电阻不计,当ab以v=4.0m/s的速度向右匀速滑动时.试求:
(1)导体ab上的感应电动势的大小.
(2)要维持ab向右匀速运行,作用在ab上的水平力为多大?
(3)电阻R上产生的焦耳热功率为多大?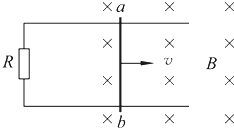
参考答案:(1)导体ab垂直切割磁感线,产生的电动势大小:
E=BLv=0.40×0.50×4.0?V=0.80?V?①
(2)导体ab相当于电源,由闭合电路欧姆定律得回路电流:
I=ER+r=0.800.20?A=4.0?A?②
导体ab所受的安培力:
F=BIL=0.40×4.0×0.50?N=0.80?N?③
由于ab匀速运动,所以水平拉力:
F′=F=0.80?N?④
(3)R上的焦耳热功率:
P=I2R=4.02×0.20?W=3.2?W?⑤
答:(1)导体ab上的感应电动势的大小为0.80V.
(2)要维持ab向右匀速运行,作用在ab上的水平力为0.80N.
(3)电阻R上产生的焦耳热功率为3.2W.
本题解析:
本题难度:一般
2、简答题 图中的匀强磁场磁感应强度B=0.5T,让长为0.2m的导体AB在金属导轨上,以5m/s的速度向左做匀速运动,设导轨两侧所接电阻R1=4Ω,R2=1Ω,本身电阻为1Ω,AB与导轨接触良好.求:
(1)导体AB中的电流大小
(2)全电路中消耗的电功率.

参考答案:(1)AB棒产生的感应电动势:E=BLv=0.5×0.2×5V=0.5V
R1与R2并联的电阻:R=R1R2R1+R2=4×14+1Ω=0.8Ω
根据闭合电路欧姆定律得:
通过AB棒的电流:I=ER+r=0.50.8+1A≈0.28A
(2)全电路中消耗的电功率:P=IE=0.5×0.28W=0.14W
答:(1)导体AB中的电流大小是0.28A.
(2)全电路中消耗的电功率是0.14W.
本题解析:
本题难度:一般
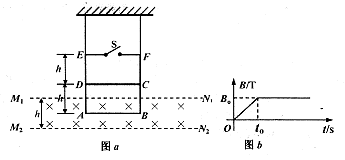
3、计算题 (20分)如图(a)所示,两条间距为h的水平虚线之间存在方向水平向里的匀强磁场,磁感应强度大小按图(b)中B-t图象变化(图中Bo已知)。现有一个“日”字形刚性金 属,线框ABCDEF,它的质量为m,EF中间接有一开关S,开关S闭合时三条水平边框的电阻均为R,其余各边电阻不计。AB=CD=EF=L,AD=DE=h。用两根轻质的绝缘细线把线框竖直悬挂住,AB边恰好在磁场区域M1 N1和M2N2的正中间,开始开关S处于断开状态。t0(未知)时刻细线恰好松弛,此后闭合开关同时剪断两根细线,当CD边刚进入磁场上边界Mi Ni时线框恰好做匀速运动(空气阻力不计)。求:
(1)t0的值;
(2)线框EF边刚离开磁场下边界M2N2时的速度;
(3)从剪断细线到线框EF边离开磁场下边界M2N2的过程中金属线框中产生的焦耳热。
参考答案:(1) (2)
(2) (3)
(3) mgh-
mgh-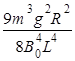
本题解析:(1)由法拉第电磁感应定律可知,感应电动势为:E=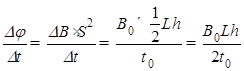 ,
,
线框中的电流:I=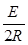 ,
,
线框受到的安培力:F=B0IL,
细线恰好松弛,细线拉力为零,
线框处于平衡状态,由平衡条件得:B0IL=mg,
解得:t0= ;
;
(2)当CD边到达M1N1时线框恰好做匀速直线运动,处于平衡状态,
由平衡条件得:B0I′L=mg,
电流I′= ,
,
CD棒切割磁感线产生的电动势:E′=B0Lv′,
解得: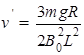 ;
;
(3)CD边到达M1N1至EF边离开磁场过程线框一直做匀速直线运动,因此EF边刚离开M2N2时,速度为:
v=v′= ,
,
由能量守恒定律得:Q=mg? h-
h-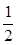 mv2=
mv2= mgh-
mgh-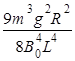 ;
;
本题难度:一般
4、选择题 当一段导线在磁场中做切割磁感线的匀速运动时,下面说法中正确的是( )
A.导线中一定有感应电流
B.导线一定受安培力作用
C.导线会产生感应电动势
D.以上说法都不正确