1、计算题 如图所示,离子发生器发射一束质量为m,电荷量为+q的离子,从静止经PQ两板间的加速电压加速后,以初速度v0再从a点沿ab方向进入一匀强电场区域,abcd所围成的正方形区域是该匀强电场的边界,已知正方形的边长为L,匀强电场的方向与ad边平行且由a指向d。
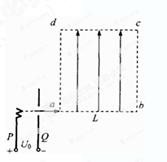
(1)求加速电压U0;
(2)若离子恰从c点飞离电场,求ac两点间的电势差Uac;
(3)若离子从边界上某点飞出时的动能为mv02,试判断离子从哪条边界飞出,并求此时匀强电场的场强大小E。
参考答案:(1)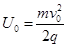 (2)
(2) (3)
(3)
本题解析::(1)对直线加速过程,根据动能定理,有: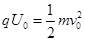 ,解得:
,解得: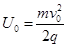
(2)设此时场强大小为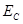 ,则:ab方向,有:
,则:ab方向,有: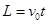 ,ad方向,有:
,ad方向,有: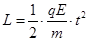
又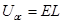 ,解得:
,解得:
(3)根据 可知,离子射出电场时的速度
可知,离子射出电场时的速度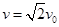 ,方向与ab所在直线的夹角为45°,即
,方向与ab所在直线的夹角为45°,即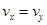 ,根据
,根据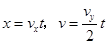 可得
可得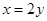 ,则离子应该从bc边上的某点飞出.
,则离子应该从bc边上的某点飞出.
ab方向,有: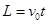 ,ad方向,有:
,ad方向,有: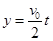 解得:
解得: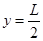
根据动能定理,有: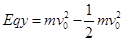
解得:
考点:考查了带电粒子在匀强电场中的运动.
本题难度:困难
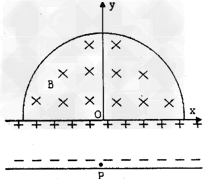
2、计算题 如图所示,在以原点O为圆心、半径为R的半圆形区域内充满了磁感应强度为B的匀强磁场,x轴下方为一平行板电容器,其正极板与x轴重合且在O处开有小孔,两极板间距离为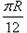 。现有电荷量为e、质量为m的电子在O点正下方负极板上的P点由静止释放。不计电子所受重力。
。现有电荷量为e、质量为m的电子在O点正下方负极板上的P点由静止释放。不计电子所受重力。
(1)若电子在磁场中运动一段时间后刚好从磁场的最右边缘处返回到x轴上,求加在电容器两极板间的电压。
(2)将两极板间的电压增大到第(1)问中电压的4倍,先在P处释放第一个电子,在这个电子刚到达O点时释放第二个电子,求第一个电子离开磁场时,第二个电子的位置坐标。
参考答案:解:(1)设加速电压为U,电子经电场加速后速度为v,由动能定理得:
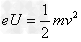 ?
?
又有 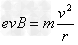 ,r =
,r =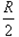
联立以上各式解得U =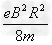
(2)电压增加为原来4倍,则有电子在磁场中的半径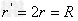
设电子在电场中运动时间为t1,加速度为a,则有
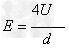 ,
,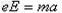
设间距为d,有: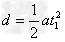
解得: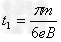 ?
?
电子在磁场中运动总时间为t2,则有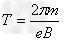 ,
,
解得: ,即
,即

由此可知:第一个电子离开磁场时,第二个电子的圆心角为30°,如图中的Q点:
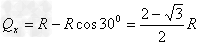

因此Q点的坐标为:
本题解析:
本题难度:困难
3、选择题 如图所示,虚线a、b和c 是某静电场中的三个等势面,它们的电势分别为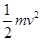 a、
a、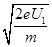 b和
b和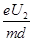 c,
c,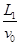 a>
a>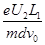 b>
b>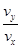 c,一带电粒子射入电场中,其运动轨迹如实线KLMN所示,由图可知(?)
c,一带电粒子射入电场中,其运动轨迹如实线KLMN所示,由图可知(?)
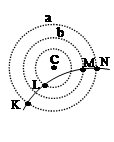
A.粒子从K到L的过程中,静电力做负功
B.粒子从L到M的过程中,静电力做负功
C.粒子从K到L的过程中,电势能增加
D.粒子从K到N的过程中,动能减小
参考答案:AC
本题解析:由带电粒子的运动轨迹可知,粒子在所受的电场力方向由场源电荷指向外,在从K到L的过程中,电场力方向与粒子运动方向成钝角,故电场力做负功,粒子的电势能增加、动能减小,所以A、C正确;同样道理,从L到M的过程中,电场力先做负功后做正功,所以B错误; K与N处于同一等势面上,故从K到N的过程中,动能先减小后增大,两点动能相等,所以D错误;
本题难度:一般
4、计算题 如图所示,在正交坐标系xOy的第一、四象限内分别存在两个大小相等、方向不同的匀强电场,两组平行且等间距的实线分别表示两个电场的电场线,每条电场线与x轴所夹的锐角均为60°.一质子从y轴上某点A沿着垂直于电场线的方向射入第一象限,仅在电场力的作用下第一次到达x轴上的B点时速度方向正好垂直于第四象限内的电场线,之后第二次到达x轴上的C点.求OB与BC的比值。
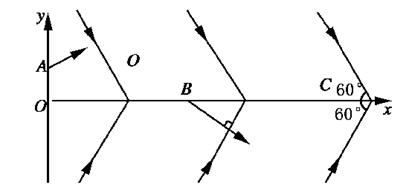
参考答案: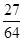
本题解析:质子的运动轨迹如图所示:
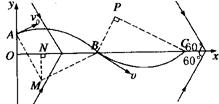
设质子在电场中运动的加速度为a,在A、B两点的速度分别为v0、v,经历时间为t1,作AM垂直于v0方向,BM平行于v0方向,过交点M作x轴的垂线,垂足为N,则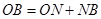
由几何关系 ?(1分)
?(1分)
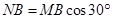 ?(1分)
?(1分)
由题意知v与v0的夹角为60°,根据平抛运动规律可知:
沿垂直于v0方向的位移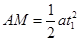 ?(1分)
?(1分)
沿平行于v0方向的位移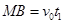 ?(1分)
?(1分)
在B点,沿垂直于v0方向的速度分量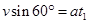 ?(1分)
?(1分)
沿平行于v0方向的速度分量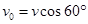 ?(1分)
?(1分)
联立解得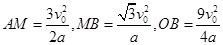 ?(1分)
?(1分)
设质子从B到C经历时间为t2,作BP垂直于v方向,CP平行于v方向,根据平抛运动规律可知:
沿PC方向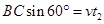 ?(1分)
?(1分)
沿BP方向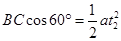 ?(1分)
?(1分)
联立解得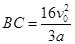
综上可知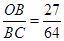 ?(2分)
?(2分)
本题难度:一般
5、计算题 如图所示,沿水平方向放置一条平直光滑槽,它垂直穿过开有小孔的两平行薄板,板相距3.5L。槽内有两个质量均为m的小球A和B,球A带电量为+2q,球B带电量为-3q,两球由长为2L的轻杆相连,组成一带电系统。最初A和B分别静止于左板的两侧,离板的距离均为L。若视小球为质点,不计轻杆的质量,在两板间加上与槽平行向右的匀强电场E后(设槽和轻杆由特殊绝缘材料制成,不影响电场的分布),求:
(1)球B刚进入电场时,带电系统的速度大小;
(2)带电系统从开始运动到速度第一次为零所需的时间及球A相对右板的位置。

参考答案:解:对带电系统进行分析,假设球A能达到右极板,电场力对系统做功为W1,有:
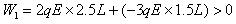
而且还能穿过小孔,离开右极板
假设球B能达到右极板,电场力对系统做功为W2,有:
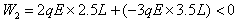
综上所述,带电系统速度第一次为零时,球A、B应分别在右极板两侧
(1)带电系统开始运动时,设加速度为a1,由牛顿第二定律: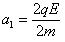 =
=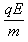
球B刚进入电场时,带电系统的速度为v1,有: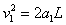
求得: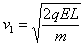
(2)设球B从静止到刚进入电场的时间为t1,则: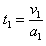
解得: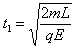
球B进入电场后,带电系统的加速度为a2,由牛顿第二定律: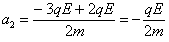
显然,带电系统做匀减速运动。设球A刚达到右极板时的速度为v2,减速所需时间为t2,则有:
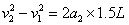 ,
,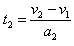
求得: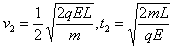
球A离电场后,带电系统继续做减速运动,设加速度为a3,再由牛顿第二定律: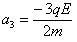
设球A从离开电场到静止所需的时间为t3,运动的位移为x,则有:
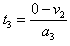 ,
,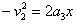
求得: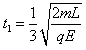 ,
,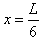
可知,带电系统从静止到速度第一次为零所需的时间为: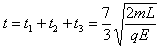
球A相对右板的位置为: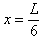
本题解析:
本题难度:困难