1、选择题  某电解池内含有等量的二价正离子和二价负离子，通电后，测得通过电解液的电流为3.2A，那么1秒钟有多少个二价正离子通过电解液的横截面 ?
A．5×1018
B．1.0×1019
C．2×1019
D．1.5×1019

参考答案：A

本题解析：正电荷移动方向与电流方向相同，负电荷移动方向与电流方向相反，如果正离子向右移动，负离子向左移动，电流为单位时间内通过横截面的电量可知1秒钟有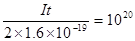个正负离子通过横截面，由于正离子数和负离子数相等，A对；

本题难度：简单

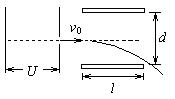
2、计算题  （18分）一束初速度不计的电子在经U的加速电压加速后，在距两极板等距处垂直进入平行板间的匀强电场，如图所示，若板间距离d，板长l，偏转电极边缘到荧光屏的距离为L，偏转电场只存在于两个偏转电极之间。已知电子质量为m，电荷量为e，求：

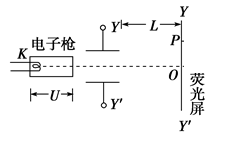
(1)电子离开加速电场是的速度大小；
(2)电子经过偏转电场的时间；
(3)要使电子能从平行板间飞出，两个极板上最多能加多大电压？
(4)电子最远能够打到离荧光屏上中心O点多远处？

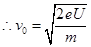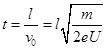参考答案：①②??③?
④离O点最远距离=" Y’+d/2=(2L+l)" d /2l

本题解析：①设电子流经加速电压后的速度为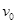，则由动能定理有：
? q=e?(2分)
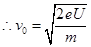?(1分)

②电子经过偏转电场时做类平抛运动，运动时间
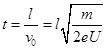? (3分)
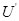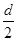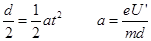③设两极板上最多能加的电压为要使电子能从平行板间飞出则电子的最大侧移量为，则有：?(4分)
联立①②两式? (2分)

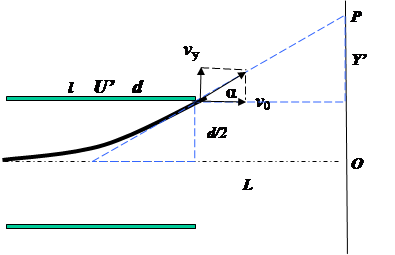
④从板边缘飞出到荧光屏上离O点最远。这时
tanα=vy/v0=Y’/L? (1分)
而vy="at" ?(1分)?∴tanα=vy/v0="U’l/2dU=" d/l? (1分)
∴Y’=" L" d/l? (1分)
离O点最远距离=" Y’+d/2=(2L+l)" d /2l? (2分)

本题难度：一般

3、选择题  如图所示，质量为m的带负电的小物块处于倾角为37°的光滑斜面上，当整个装置处于竖直向下的匀强电场中时，小物块恰处于静止。现将电场方向突然改为水平向右，而场强大小不变，则

A．小物块仍静止
B．小物块沿斜面加速上滑
C．小物块沿斜面加速下滑
D．小物块将脱离斜面运动

参考答案：C

本题解析：当整个装置处于竖直向下的匀强电场中时，小物块恰处于静止,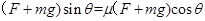。如果电场水平向右，电场力水平向左，则一定有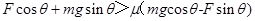，所以物体沿斜面加速下滑。答案选C。

本题难度：一般

4、计算题  如图所示，质量为为m、电量为q的带电粒子，经电压为U加速，又经磁感应强度为B的匀强磁场后落到图中D点，求：
（1）带电粒子在A点垂直射入磁场区域时的速率v；
（2）A、D两点间的距离l。

参考答案：解：（1）带电粒子在电场中直线加速，电场力做功，动能增加，由动能定理可知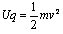
带电粒子垂直射入磁场区域时的速率为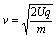
（2）带电粒子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，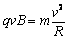
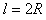
解得A、D两点间的距离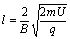

本题解析：

本题难度：一般

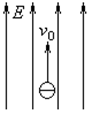
5、计算题  （8分）一个电子以v0＝4×107m/s的速度，方向与电场方向相同，射入电场强度E＝2×105V/m的匀强电场中，如图所示，已知电子电量－e＝－1.6×10－19C，电子质量m＝9.1×10－31kg.。试求：
（1）从电子的入射点到达速度为0之点的两点间电势差是多少? 两点间距离是多少?
（2）电子速度减小为0所需的时间是多少?

参考答案：（1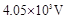），0.2m；（2）。

本题解析：（1）?，?；，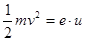
（2）
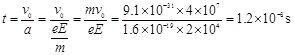
本题考查电荷在电场中的加速，在电场中运动时，由电场力做功eU和动能定理可求得电势差大小，再由U=Ed可求得两点之间距离，由电场力提供加速度，粒子做匀加速直线运动，由v=at可求得运动时间

本题难度：一般