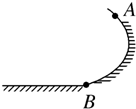
1、选择题  如图所示，一个质量为m的物体从高为h的曲面上一点A处，由静止开始下滑，滑到水平面上B点处停止.若再用平行于接触面的力将该物体从B处拉回到原出发点A处，则需要对物体做功的最小值为（　　）

A．mgh
B．2mgh
C．1.5mgh
D．3mgh

参考答案：B

本题解析：物体由A滑到B时，动能的变化为0，而重力做功为mgh，设摩擦力做的功为Wf，则由动能定理可得，mgh+Wf=0，即Wf=－mgh；如果物体再由B到A，设水平力做的功为W，则W+Wf+(－mgh)=0；故解得W=mgh－Wf=2mgh，B是正确的。

本题难度：一般

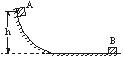
2、选择题  轻质弹簧右端固定在墙上，左端与一质量m=0.5kg的物块相连，如图甲所示。弹簧处于原长状态，物块静止且与水平面间的动摩擦因数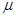=0.2。以物块所在处为原点，水平向右为正方向建立x轴。现对物块施加水平向右的外力F，F随x轴坐标变化的情况如图乙所示。物块运动至x=0.4m处时速度为零。则此时弹簧的弹性势能为(g=10m/S2)

A．3.1 J
B．3.5 J
C．1.8 J
D．2.0J

参考答案：A

本题解析：对m受力分析，受到重力G、支持力N、外力F、和摩擦力f以及弹力F’，m在向右运动过程中，外力F做正功，摩擦力f做负功，弹力F’做负功，三个力做功之和等于物体m的动能变化，即WF-Wf –W’=0，其中WF=WF1+WF2=(5+10)×0.2/2+10×0.2J=3.5J,而Wf=?mgx=0.5J，所以弹力做功W’=3.1J，而弹力做的功等于弹性势能的变化，所以弹性势能为EP=3.1J。则A选项正确。

本题难度：一般

3、简答题  某人在距离地面2.6m的高处，将质量为0.2kg的小球以v0=12m/s速度斜向上抛出，小球的初速度方向与水平方向之间的夹角为30°，g取10m/s2，求：
（1）人抛球时对球做多少功？
（2）若不计空气阻力，小球落地时的速度大小是多少？
（3）若小球落地时的速度大小为v1=13m/s，小球在空中运动过程中克服阻力做了多少功？

参考答案：（1）由动能定理得：W=△EK=12mv02=14.4J；
（2）在小球的整个运动过程中，由动能定理得：
mgh=12mv2-12mv02，解得：v=14m/s；
（3）在整个运动过程中，由动能定理得：
mhg-Wf=12mv12-12mv02，解得：Wf=2.7J；
答：（1）人抛球时对球做14.4J的功；
（2）若不计空气阻力，小球落地时的速度为14m/s；
（3）若小球落地时的速度大小为v1=13m/s，小球在空中运动过程中克服阻力做了2.7J的功．

本题解析：

本题难度：一般

4、计算题  （19分）如图，用跨过光滑定滑轮的缆绳将海面上一搜失去动力的小船沿直线拖向岸边。已知拖动缆绳的电动机功率恒为P，小船的质量为m，小船受到的阻力大小恒为f，经过A点时的速度大小为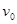，小船从A点沿直线加速运动到B点经历时间为t1，A、B两点间距离为d,缆绳质量忽略不计。求：

（1）小船从A点运动到B点的全过程克服阻力做的功；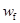
（2）小船经过B点时的速度大小；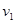
（3）小船经过B点时的加速度大小a。

参考答案：（1）
（2）
（3）

本题解析：（1）：小船从A点到达B点，受到的阻力恒为f,其克服阻力做的功为：
（2）：从A到B由动能定理可知：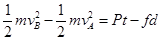
解得：
（3）设小船经过B点时绳的拉力大小为F，绳与水平方向夹角为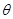，电动机牵引绳的速度大小为u，则P=Fu

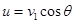
由牛顿第二定律有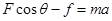
解得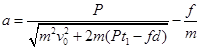

本题难度：简单

5、选择题  滑板是现在非常流行的一种运动，如图所示，一滑板运动员以7m/s的初速度从曲面的A点下滑，运动到B点速度仍为7m/s，若他以6m/s的初速度仍由A点下滑，则他运动到B点时的速度（　　）
A．大于6m/s
B．等于6m/s
C．小于6m/s
D．条件不足，无法计算