1、计算题  在xoy平面直角坐标系的第Ⅰ象限有射线OA，OA与x轴正方向夹角为30°，如图所示，OA与y轴所夹区域存在y轴负方向的匀强电场，其它区域存在垂直坐标平面向外的匀强磁场；有一带正电粒子质量m，电量q，从y轴上的P点沿着x轴正方向以大小为v0的初速度射入电场，运动一段时间沿垂直于OA方向经过Q点进入磁场，经磁场偏转，过y轴正半轴上的M点再次垂直进入匀强电场。已知OP = h，不计粒子的重力。

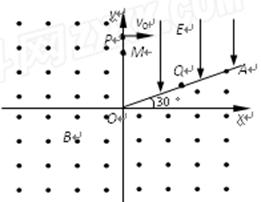
⑴ 求粒子垂直射线OA经过Q点的速度vQ；
⑵ 求匀强电场的电场强度E与匀强磁场的磁感应强度B的比值；
⑶ 粒子从M点垂直进入电场后，如果适当改变电场强度，可以使粒子再次垂直OA进入磁场，再适当改变磁场的强弱，可以使粒子再次从y轴正方向上某点垂直进入电场；如此不断改变电场和磁场，会使粒子每次都能从y轴正方向上某点垂直进入电场，再垂直OA方向进入磁场……，求粒子从P点开始经多长时间能够运动到O点？

2、计算题  （10分）如图，在平面直角坐标系xOy内，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限以ON为直径的半圆形区域内，存在垂直于坐标平面向外的匀强磁场，磁感应强度大小为B。一质量为m、电荷量为q的带正电的粒子，从y轴正半轴上y = h处的M点，以速度v0垂直于y轴射入电场，经x轴上x = 2h处的P点进入磁场，最后以垂直于y轴的方向射出磁场。不计粒子重力。求

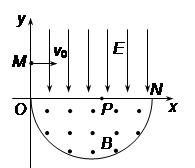
（1）电场强度大小E；
（2）粒子在磁场中运动的轨道半径r；
（3）粒子从进入电场到离开磁场经历的总时间t。

3、计算题  如图所示，真空中有一以(r，0)为圆心、半径为r的圆柱形匀强磁场区域，磁场的磁感应强度大小为B方向垂直纸面向里，在y≥r的范围内，有方向向左的匀强电场，电场强度大小E。从O点向不同方向发射速率相同的质子，质子的运动轨迹均在纸面内，已知质子的电量为e，质量为m，质子在磁场中的偏转半径也为r，不计重力及阻力作用。求：
(1)质子进入磁场时的速度大小；
(2)速度方向沿x轴正方向射入磁场的质子，到达y轴所需的时间；
(3)速度方向与x轴正方向成30°角（如图中所示）射入磁场的质子，到达y轴时的位置坐标。

4、计算题  如图所示，abcd构成一个边长为L的正方形区域，在ac连线的右下方存在场强大小为E、方向垂直于ad向上的匀强电场，在?abc区域内(含边界)存在方向垂直于纸面向里的匀强磁场，在?abc区域外、ac连线的左上方存在方向垂直于纸面向外的匀强磁场，两磁场区域的磁感应强度大小相等.现有两个可视为质点、质量均为m、电荷量均为q的带正电粒子同时从a点射出，粒子甲的初速度方向由a指向d，粒子乙的初速度方向由a指向c，当乙经b到达c点时，刚好与只在电场中运动的甲相遇.若空间为真空，不计粒子重力和粒子间的相互作用力，忽略粒子运动对电、磁场产生的影响。求：

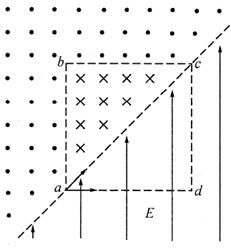
（1）甲的速率v甲和甲从a到c经历的时间t。
（2）乙的速率v乙和磁感应强度大小B满足的条件。

5、简答题  （17分）
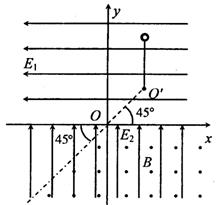
如图所示，在x轴上方有水平向左的匀强电场，电场强度为E1；下方有竖直向上的匀强电场，电场强度为E2，且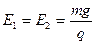。在x轴下方的虚线（虚线与茗轴成45°角）右侧有垂直纸面向外的匀强磁场，磁感应强度为B。有一长为L的轻绳一端固定在第一象限内的O′点，且可绕O′点在竖直平面内转动；另一端拴有一质量为m的小球，小球带电量为+q。OO′与x轴成45°角，其长度也为L。先将小球放在O′点正上方，从绳恰好绷直处由静止释放，小球刚进人有磁场的区域时将绳子断开。
试求：
（1）绳子第一次刚拉直还没有开始绷紧时小球的速度大小；
（2）小球刚进入有磁场的区域时的速度大小；
（3）小球从进入有磁场的区域到第一次打在x轴上经过的时间。