1、选择题  光滑水平面上半径相等的两金属小球A和B相向运动并发生对心碰撞，碰后两球均静止，若两球的质量之比为mA：mB=1：3，则两球碰前的速度关系为（　　）
A．方向相同，大小之比为1：3
B．方向相同，大小之比为3：1
C．方向相反，大小之比为1：3
D．方向相反，大小之比为3：1

参考答案：根据动量守恒，设A球初速度方向为正方向：
mAvA-mBvB=0，
得：vAvB=mBmA=31，
D正确．
故选：D．

本题解析：

本题难度：一般

2、实验题  如图所示，质量为m、半径为R的小球，放在半径为2R、质量为2m的大空心球内．大球开始静止在光滑的水平面上，当小球从图示位置无初速度沿大球内壁滚到最低点时，大球移动的距离是___________．

参考答案：s＝

本题解析：设大球运动的位移为s，由图3知小球运动的位移为(R－s)
由“人船模型”知两球在水平方向动量守恒，因此有　m(R－s)＝2ms 解得：s＝

本题难度：简单

3、计算题  （11分）如图（1）所示，在光滑的水平面上有甲、乙两辆小车，质量为30kg的小孩乘甲车以5m/s的速度水平向右匀速运动，甲车的质量为15kg，乙车静止于甲车滑行的前方，两车碰撞前后的位移随时间变化图象如图（2）所示。

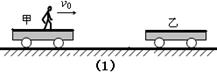
求：（1）甲乙两车碰撞后的速度大小；
（2）乙车的质量；
（3）为了避免甲乙两车相撞，小孩至少以多大的水平速度从甲车跳到乙车上？

参考答案：（1）甲车的速度大小为，乙车的速度大小为v2=3m/s
（2）
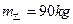
（3）

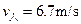
本题解析：（1）由图可知，碰撞后甲车的速度大小为?（1分）
乙车的速度大小为v2="3m/s?" （1分）
（2）在碰撞过程中，三者组成的系统满足动量守恒。
?（2分）
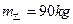解得：?（1分）
（3）设人跳向乙车的速度为v人,由动量守恒定律得
人跳离甲车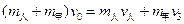：?（1分）
人跳至乙车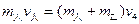：?（1分）
为使二车避免相撞，应满足?（2分）
?
取“=”时，人跳离甲车的速度最小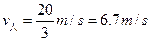，?（2分）

本题难度：简单

4、选择题  光滑水平面上两小球甲、乙用不可伸长的松驰细绳相连。开始时甲球静止，乙球以一定速度运动直至绳被拉紧，然后两球一起运动，在此过程中两球的总动量和机械能的变化情况是
A．动量守恒，机械能不守恒
B．动量守恒，机械能守恒
C．动量不守恒，机械能守恒
D．动量不守恒，机械能不守恒

参考答案：A

本题解析：以两物体为研究对象可知所受合外力为零，则符合动量守恒条件，但是在绳子拉直过程中会有机械能的损失，所以选A

本题难度：简单

5、计算题  （20分）某兴趣小组设计了一种实验装置，用来研究碰撞问题，其模型如题图所示不用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔，从左到右，球的编号依次为1、2、3……N，球的质量依次递减，每球质量与其相邻左球质量之比为k（k＜1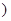.将1号球向左拉起，然后由静止释放，使其与2号球碰撞，2号球再与3号球碰撞……所有碰撞皆为无机械能损失的正碰.（不计空气阻力，忽略绳的伸长，g取10 m/s2）

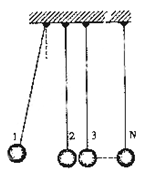
（1）设与n+1号球碰撞前，n号球的速度为vn,求n+1号球碰撞后的速度.
（2）若N＝5,在1号球向左拉高h的情况下，要使5号球碰撞后升高16k（16 h小于绳长）问k值为多少？
（3）在第（2）问的条件下，悬挂哪个球的绳最容易断，为什么？

参考答案：（1）vn-1=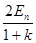
（2）k=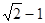
（3）悬挂1号球的绳最容易断.

本题解析：（1）设n号球质量为m,n+1，碰撞后的速度分别为取水平向右为正方向，据题意有n号球与n+1号球碰撞前的速度分别为vn、0、mn+1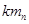
根据动量守恒，有?（1）
根据机械能守恒，有=?（2）?
由（1）、（2）得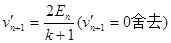
设n+1号球与n+2号球碰前的速度为En+1
据题意有vn-1=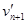
得vn-1=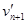=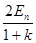?（3）
（2）设1号球摆至最低点时的速度为v1,由机械能守恒定律有
?（4）
v1=?（5）
同理可求，5号球碰后瞬间的速度
?（6）
由（3）式得?（7）
N=n=5时，v5=?（8）
由（5）、（6）、（8）三式得
k=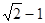?（9）
（3）设绳长为l,每个球在最低点时，细绳对球的拉力为F,由牛顿第二定律有
?（10）
则?（11）
（11）式中Ekn为n号球在最低点的动能
由题意1号球的重力最大，又由机械能守恒可知1号球在最低点碰前的动能也最大，根据（11）式可判断在1号球碰前瞬间悬挂1号球细绳的张力最大，故悬挂1号球的绳最容易断.

本题难度：一般