1、简答题  某直角坐标系中，在第四象限有一平行与X轴正方向相同的匀强电场，其余的所有区域也存在同样大小的匀强电场，但方向与Y轴正方向相同，同时在X轴的正半轴有垂直纸面向里的匀强磁场．现一质量m、电量q的电荷以速度v，45°夹角进入该直角坐标系中，如图所示，先做直线运动，后做曲线运动与X轴垂直相交于B点．
（1）判断电荷的电性，
（2）电场强度和磁场强度的大小分别是多少
（3）AB间的距离是多少
（4）为了让电荷能做周期性的运动，在X轴的负半轴设计了一个有界的匀强磁场即可，试求此磁场的面积．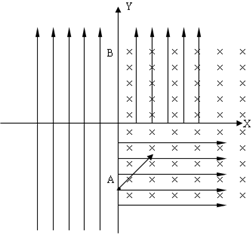

参考答案：（1）电荷在开始阶段做直线运动，受到重力、电场力和洛伦兹力，重力、电场力是恒力，电荷只有做匀速直线运动，说明电荷带正电．
? （2）根据平衡条件得
? qE=mg，得E=mgq
? 由qvB=

本题解析：

本题难度：一般

2、填空题  某同学在“用打点计时器测量匀变速直线运动的加速度”实验中，用打点计时器记录了被小车拖动的纸带的运动情况，并在纸带上确定出A、B、C、D、E、F、G共7个计数点，相邻的两个计数点间均有4个点未画出．其相邻计数点间的距离如图所示，打点计时器使用的是50Hz的交流电．根据纸带回答下列问题：

（1）计时器打下从A到G这一段小车的平均速度为______m/s．
（2）计时器打下B点时的瞬时速度为______m/s．这一段小车的加速度为______m/s2（以上结果全部保留两位有效数字）

参考答案：（1）由于每相邻两个计数点间还有4个点没有画出，所以相邻的计数点间的时间间隔T=0.1s，
计时器打下从A到G这一段小车的平均速度为.v=XAGtAG=0.0362+0.0438+0.0520+0.0599+0.0680+0.07626×0.1=0.56m/s
（2）根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上B点时小车的瞬时速度大小．
vB=XAC2T=0.0362+0.04380.2=0.40m/s
设A到B之间的距离为x1，以后各段分别为x2、x3、x4、x5、x6，
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，得：
x4-x1=3a1T2
x5-x2=3a2T2
x6-x3=3a3T2
为了更加准确的求解加速度，我们对三个加速度取平均值
得：a=13（a1+a2+a3）=XDG-XAD9T2=(7.62+6.80+5.99)cm-(3.62+4.38+5.20)×0.01m9×(0.1s)2=0.80m/s2
故答案为：
（1）0.56
（2）0.40，0.80

本题解析：

本题难度：一般

3、填空题  做匀速圆周运动的物体，当质量增大到2倍，周期减小到一半时，其向心力大小是原来的______倍，当质量不变，线速度大小不变，角速度大小增大到2倍时，其向心力大小是原来的______倍。

参考答案：8，2

本题解析：

本题难度：一般

4、简答题  如图所示，在同一条竖直线上，有电荷量均为Q的A、B两个正点电荷，；?GH是它们连线的垂直平分线．另有一个带电小球C，质量为m、电荷量为+q（可视为点电荷），被长为L的绝缘轻细线悬挂于O点，现在把小球C拉起到M点，使细线水平且与?A、B处于同一竖直面内，由静止开始释放，小球C向下运动到GH线上的N点时刚好速度为零，此时细线与竖直方向的夹角θ=30°．试求：
（1）在A、B所形成的电场中，M、N两点间的电势差，并指出M、N哪一点的电势高．
（2）若N点与A、B两个点电荷所在位置正好形成一个边长为a的正三角形，则小球运动到N
点瞬间，轻细线对小球的拉力FT（静电力常量为k）

参考答案：

（1）带电小球C在A、B形成的电场中从M点运动到N点的过程中，重力和电场力做功，但合力功为零，则
qUMN+mglcosθ=0
所以UMN=-mglcos30°q
即M、N两点间的电势差大小mglcos30°q，
且N点的电势高于M点的电势．
（2）在N点，小球C受到重力mg、细线的拉力FT以及A和B分别对它的斥力FA和FB四个力的作用如图所示，且沿细线方向的合力为零．
则FT-mgcos30°-FAcos30°=0
又FA=FB=kQqa2
得FT=mgcos30°+kQqa2cos30°
答：（1）在A、B所形成的电场中，M、N两点间的电势差为mglcos30°q，N点的电势高于M点的电势；
（2）小球运动到N点瞬间，轻细线对小球的拉力FT为mgcos30°+kQqa2cos30°．

本题解析：

本题难度：一般

5、选择题  如图所示，汽车在一段弯曲水平路面上匀速率行驶，关于它受到的水平方向的作用力方同的示意图，可能正确的是（图中F为地面对其的静摩擦力，f为它行驶时所受阻力）（　　）
A．

B．

C．

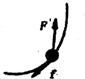
D．