1、选择题  根据牛顿第二定律，下列叙述正确的是
A．物体加速度的方向可能跟它所受合力的方向相反
B．物体所受合力必须达到一定值时，才能使物体产生加速度
C．物体加速度的大小跟它所受的任一个力的大小都成正比
D．当物体的质量改变时，若所受合力的水平分力不变，则物体水平加速度大小与其质量成反比

参考答案：D

本题解析：由F=ma可知合外力的方向与加速度方向相同，A错；力是产生加速度的原因，力与加速度变化具有瞬时性，B错；物体加速度大小与物体所受合外力成正比，C错；当物体的质量改变时，若所受合力的水平分力不变，则物体水平加速度大小与其质量成反比，D对；故选D
点评：难度较小，由F=ma理解F与a的关系，F与m的关系

本题难度：简单

2、计算题  如图所示，质量为80kg的物体放在安装在小车上的水平磅秤上，已知斜面的倾角θ为37°，小车与斜面间的动摩擦因数为0.25，现小车沿斜面向下运动，则磅秤的读数为多少？物体对磅秤的静摩擦力为多少？（sin37°=0.6，cos37°=0.8，g取10m/s2）

参考答案：解：取小车、物体、磅秤这个整体为研究对象，受总重力Mg、斜面的支持力FN
由牛顿第二定律得，Mgsinθ-μMgcosθ=Ma，a=gsinθ-μgcosθ，解得a=4m/s2
取物体为研究对象，受力情况如图所示，将加速度a沿水平和竖直方向分解，则有

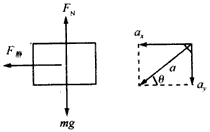
F静=macosθ，mg-FN=masinθ，解得FN=608N，F静=256N
根据牛顿第三定律，物体对磅秤的静摩擦力为256N，方向水平向右

本题解析：

本题难度：一般

3、简答题  如图（a）所示，平行金属导轨MN、PQ光滑且足够长，固定在同一水平面上，两导轨间距L=0.25m，电阻R=0.5Ω，导轨上停放一质量m=0.1kg、电阻r=0.1Ω的金属杆，导轨电阻可忽略不计，整个装置处于磁感强度B=0.4T的匀强磁场中，磁场方向竖直向下，现用一外力F沿水平方向拉杆，使其由静止开始运动，理想电压表的示数U随时间t变化的关系如图（b）所示．试分析与求：

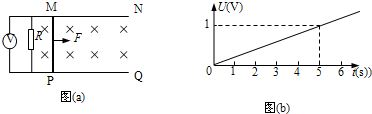
（1）分析证明金属杆做匀加速直线运动；
（2）求金属杆运动的加速度；
（3）写出外力F随时间变化的表达式；
（4）求第2.5s末外力F的瞬时功率．

参考答案：
（1）U=ε?RR+r=BLvRR+r，
U∝v，因U随时间均匀变化，
故v也随时间均匀变化，金属杆做匀加速直线运动．?
（2）k=△U△t=△v△t?BLRR+r=a?BLRR+r
解得：a=k(R+r)BLR=0.2×(0.5+0.1)0.4×0.25×0.5=2.4（m/s2）?
（3）F=F安+ma=BIL+ma=B2L2atR+r+ma=0.04t+0.24
（4）P=Fv=（0.04t+0.24）at=2.04W?
答：（1）因U随时间均匀变化，故v也随时间均匀变化，金属杆做匀加速直线运动；
（2）则金属杆运动的加速度2.4m/s2；
（3）外力F随时间变化的表达式为F=0.04t+0.24；
（4）则第2.5s末外力F的瞬时功率2.04W．

本题解析：

本题难度：一般

4、简答题  一根质量为M的木棒,上端用细绳系在天花板上,棒上有一质量为m的猴子,如图所示.如将绳子剪断,猴子沿棒向上爬,仍保持与地面间的高度不变,求这时木棒下落的加速度.

参考答案：?方向向下

本题解析：猴子与地面间的高度不变,则Ff=mg
对杆:Ff′+Mg=Ma,Ff=Ff′
所以木棒的加速度a=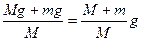,方向向下.

本题难度：简单

5、选择题  如图所示，一个小球从高处自由下落到达A点与一个轻质弹簧相撞，弹簧被压缩．在球与弹簧接触，到弹簧被压缩到最短的过程中，关于球的动能、重力势能、弹簧的弹性势能的说法中正确的是（　　）
A．球的动能一直在减小
B．球的动能先增大后减小
C．球的重力势能逐渐减小，弹簧的弹性势能逐渐增加
D．球的重力势能和弹簧的弹性势能之和逐渐增加