1、简答题 将导体放在沿x方向的匀强磁场中,导体中通有沿y方向的电流时,在导体的上下两侧面间会出现电势差,这个现象称为霍尔效应.利用霍尔效应的原理可以制造磁强计,测量磁场的磁感应强度.
磁强计的原理如图所示,电路中有一段金属导体,它的横截面为边长等于a的正方形,放在沿x正方向的匀强磁场中,导体中通有沿y方向、电流强度为I的电流,已知金属导体单位体积中的自由电子数为n,电子电量为e,金属导体导电过程中,自由电子所做的定向移动可以认为是匀速运动,测出导体上下两侧面间的电势差为U.求:
(1)导体上、下侧面那个电势较高?
(2)磁场的磁感应强度是多少?
参考答案:(1)根据左手定则知,电子向下侧偏转,则导体下表面电势较低,上侧电势高.
(2)自由电子做定向移动,视为匀速运动,速度设为v,有I=nea2v
电子受电场力和洛伦兹力平衡,有eUa=Bev
解得B=neaUI.
答:(1)上侧电势高.
(2)磁场的磁感应强度是neaUI.
本题解析:
本题难度:一般
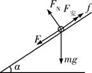
2、计算题 (12分)足够长的平行金属导轨MN和PK表面粗糙,与水平面之间的夹角为α,间距为L。垂直于导轨平面向上的匀强磁场的磁感应强度为B,MP间接有阻值为R的电阻,质量为m的金属杆ab垂直导轨放置,其他电阻不计。如图所示,用恒力F沿导轨平面向下拉金属杆ab,使金属杆由静止开始运动,杆运动的最大速度为vm,t s末金属杆的速度为v1,,前t s内金属杆的位移为x,(重力加速度为g)求:
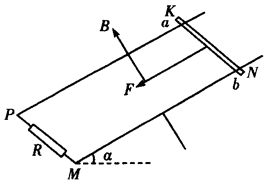
(1)金属杆速度为v1时加速度的大小;
(2)整个系统在前t s内产生的热量。
参考答案:(1) (2)
(2)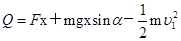
本题解析:金属杆运动过程中,沿斜面方向有自身重力沿斜面向下的分力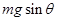 ,沿斜面向下的拉力F,沿斜面向上的摩擦力f和安培力BIL, 当杆运动的速度为
,沿斜面向下的拉力F,沿斜面向上的摩擦力f和安培力BIL, 当杆运动的速度为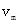 时,为匀速运动
时,为匀速运动
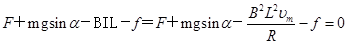
得到
当杆的速度为 v1 时,有
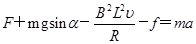
解得 ?
?
(2)t s 末金属杆的速度为 v1,前 t s 内金属杆的位移为 x 。
安培力做功全部转化为电能发热,根据动能定理有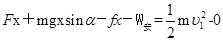
所以焦耳热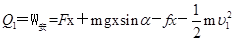
摩擦生热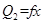
整个系统在前t s内产生的热量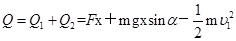
本题难度:一般
3、计算题 (12分)如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一个压敏电阻元件,其阻值与其两端所加电压成正比,即R=kU,式中k为已知的常数.框架上有一质量为m,离地高为h的金属棒,金属棒与框架始终接触良好无摩擦,且保持水平,磁感应强度为B的匀强磁场,方向垂直于框架平面向里.今将金属棒由静止释放,棒沿框架向下运动,不计金属棒电阻,重力加速度为g.试求:

(1)金属棒运动过程中,流过棒的电流大小和方向;
(2)金属棒落到地面时的速度大小;
(3)金属棒从释放到落地过程中通过电子元件的电量.
参考答案:(1)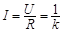 (从a→b)(2)
(从a→b)(2) (3)
(3)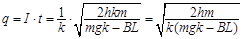
本题解析:(1)流过电阻R的电流大小为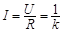 ?(2分)
?(2分)
电流方向水平向右(从a→b)?(1分)
(2)在运动过程中金属棒受到的安培力为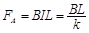 ?(1分)?
?(1分)?
对金属棒运用牛顿第二定律,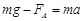 ?(1分)?
?(1分)?
得: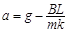 恒定,金属棒作匀加速直线运动 (2分)?
恒定,金属棒作匀加速直线运动 (2分)?
由 ,得:
,得: ?(1分)?
?(1分)?
(3)设金属棒经过时间t落地,由: ?得:
?得: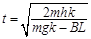 (2分)
(2分)
所求电量: (2分)
(2分)
点评:本题难度中等,特别注意的是压敏电阻的阻值是变化的,由电压与电阻的关系可知流过电阻R的电流恒定不变,因此导体棒的加速度不变,与常规题思路刚好相反
本题难度:一般
4、计算题 如图(甲)所示的轮轴,它可以绕垂直于纸面的光滑固定水平轴O转动。轮上绕有轻质柔软细线,线的一端系一重物,另一端系一质量为m的金属杆。在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF,在QF之间连接有阻值为R的电 阻,其余电阻不计,磁感应强度为B的匀强磁场与导轨平面垂直。开始时金属杆置于导轨下端,将质量为M的重物由静止释放,重物最终能匀速下降。运动过程中金属杆始终与导轨垂直且接触良好,忽略所有摩擦。
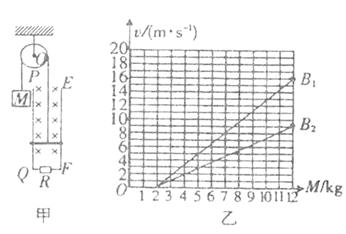
(1)重物匀速下降的速度V的大小是多少?
(2)对一定的磁感应强度B,重物的质量M取不同的值,测出相应的重物做匀速运动时的速度,可得出v-M实验图线。图(乙)中画出了磁感应强度分别为B1和B2时的两条实验图线,试根据实验结果计算B1和B2的比值。
(3)若M从静止到匀速的过程中一目下降的高度为h,求这一过程中R上产生的焦耳热
参考答案:(1) ? (2)
? (2)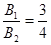 ? (3)
? (3)
本题解析:重物匀速下降时,金属杆匀速上升,合力为零.由F=BIL、 、E=BLv,结合平衡条件求出重物匀速下降的速度v,再根据v的表达式,分析v-M图象的斜率,结合图象求出斜率,即可得到B1和B2的比值.M从静止到匀速的过程中下降高度h的过程中,M的重力势能减小转化为m的重力势能、系统的动能和内能,可根据能量守恒定律求解R上产生的焦耳热.
、E=BLv,结合平衡条件求出重物匀速下降的速度v,再根据v的表达式,分析v-M图象的斜率,结合图象求出斜率,即可得到B1和B2的比值.M从静止到匀速的过程中下降高度h的过程中,M的重力势能减小转化为m的重力势能、系统的动能和内能,可根据能量守恒定律求解R上产生的焦耳热.
金属杆达到匀速运动时,受绳子拉力F、金属杆的重力mg、向下的安培力FA.
则:F=FA+mg?①
其中 F=Mg?②
又对金属杆有:安培力FA=BIL,感应电流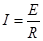 ,感应电动势E=BLv,
,感应电动势E=BLv,
则 ?③
?③
由①②③得 
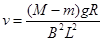 。
。
(2) 由第一题结果及题意可得v-M的函数关系式为
结合图线可知,斜率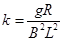 ?
?
所以
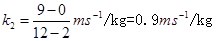
因此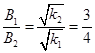
(3)由能量关系,在这个过程中R上产生的焦耳热为

将v代入可得:
本题难度:一般
5、选择题 在同时存在匀强电场和匀强磁场的空间中取正交坐标系Oxyz(y轴正方向竖直向上),如图所示。已知电场方向沿y轴正方向,场强大小为E;磁场方向沿z轴正方向,磁感应强度的大小为B;重力加速度为g。一质量为m、带电量为+q的带电微粒从原点以速度v出发。关于它在这一空间的运动的说法正确的是
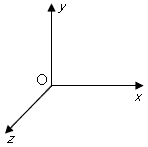
[? ]
A. 一定能沿x轴做匀速运动
B. 一定沿y轴做匀速运动
C. 可能沿y轴做匀速运动
D. 可能沿z轴做匀速运动
参考答案:D
本题解析:
本题难度:一般
Animals are such agreeable friends-they ask no questions,they pass no criticisms. 动物是极容易相处的朋友,它们从不提问,也从不会批评。