1、简答题 将导体放在沿x方向的匀强磁场中,导体中通有沿y方向的电流时,在导体的上下两侧面间会出现电势差,这个现象称为霍尔效应.利用霍尔效应的原理可以制造磁强计,测量磁场的磁感应强度.
磁强计的原理如图所示,电路中有一段金属导体,它的横截面为边长等于a的正方形,放在沿x正方向的匀强磁场中,导体中通有沿y方向、电流强度为I的电流,已知金属导体单位体积中的自由电子数为n,电子电量为e,金属导体导电过程中,自由电子所做的定向移动可以认为是匀速运动,测出导体上下两侧面间的电势差为U.求:
(1)导体上、下侧面那个电势较高?
(2)磁场的磁感应强度是多少?
2、计算题 (12分)足够长的平行金属导轨MN和PK表面粗糙,与水平面之间的夹角为α,间距为L。垂直于导轨平面向上的匀强磁场的磁感应强度为B,MP间接有阻值为R的电阻,质量为m的金属杆ab垂直导轨放置,其他电阻不计。如图所示,用恒力F沿导轨平面向下拉金属杆ab,使金属杆由静止开始运动,杆运动的最大速度为vm,t s末金属杆的速度为v1,,前t s内金属杆的位移为x,(重力加速度为g)求:
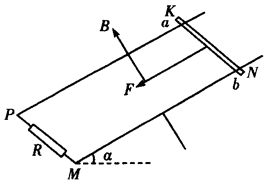
(1)金属杆速度为v1时加速度的大小;
(2)整个系统在前t s内产生的热量。
3、计算题 (12分)如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一个压敏电阻元件,其阻值与其两端所加电压成正比,即R=kU,式中k为已知的常数.框架上有一质量为m,离地高为h的金属棒,金属棒与框架始终接触良好无摩擦,且保持水平,磁感应强度为B的匀强磁场,方向垂直于框架平面向里.今将金属棒由静止释放,棒沿框架向下运动,不计金属棒电阻,重力加速度为g.试求:

(1)金属棒运动过程中,流过棒的电流大小和方向;
(2)金属棒落到地面时的速度大小;
(3)金属棒从释放到落地过程中通过电子元件的电量.
4、计算题 如图(甲)所示的轮轴,它可以绕垂直于纸面的光滑固定水平轴O转动。轮上绕有轻质柔软细线,线的一端系一重物,另一端系一质量为m的金属杆。在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF,在QF之间连接有阻值为R的电 阻,其余电阻不计,磁感应强度为B的匀强磁场与导轨平面垂直。开始时金属杆置于导轨下端,将质量为M的重物由静止释放,重物最终能匀速下降。运动过程中金属杆始终与导轨垂直且接触良好,忽略所有摩擦。
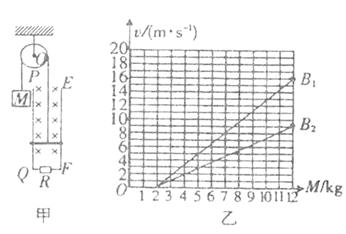
(1)重物匀速下降的速度V的大小是多少?
(2)对一定的磁感应强度B,重物的质量M取不同的值,测出相应的重物做匀速运动时的速度,可得出v-M实验图线。图(乙)中画出了磁感应强度分别为B1和B2时的两条实验图线,试根据实验结果计算B1和B2的比值。
(3)若M从静止到匀速的过程中一目下降的高度为h,求这一过程中R上产生的焦耳热
5、选择题 在同时存在匀强电场和匀强磁场的空间中取正交坐标系Oxyz(y轴正方向竖直向上),如图所示。已知电场方向沿y轴正方向,场强大小为E;磁场方向沿z轴正方向,磁感应强度的大小为B;重力加速度为g。一质量为m、带电量为+q的带电微粒从原点以速度v出发。关于它在这一空间的运动的说法正确的是
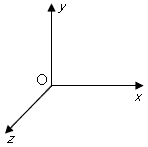
[? ]
A. 一定能沿x轴做匀速运动
B. 一定沿y轴做匀速运动
C. 可能沿y轴做匀速运动
D. 可能沿z轴做匀速运动