1、选择题  初速度为零的下列粒子，经电压为U的同一加速电场加速后，动能最大的是
A．质子（）
B．α粒子（）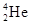
C．钠离子（）
D．铝离子（）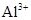

参考答案：D

本题解析：由动能定理，粒子经过同一加速电场加速后，动能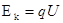，动能的大小由粒子所带电量多少决定，故D正确

本题难度：简单

2、选择题  (7分)如图所示，质量m=2.0kg的金属块(可视为质点)静止在高h=1.8m的光滑水平台面上。现用水平恒力F=9.0N拉动金属块，当金属块向右运动s=4.0m时撤去拉力F，之后金属块在台面上滑行一段距离后飞离台面。空气阻力忽略不计，g取10m/s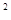。求：

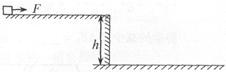
(1)金属块离开台面时的速度大小v；
(2)金属块落地点距台面边缘的水平距离L；
(3)金属块落地时速度方向与竖直方向的夹角θ。

参考答案：（1）6m/s(2)3.6m?（3）?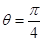

本题解析：金属块在台面上滑行过程中，只有拉力F=9N做功，根据动能定理，解得金属块离开台面时的速度?离开台面后做平抛运动，竖直方向自由落体运动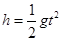时间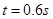，水平方向匀速直线运动水平位移?。平抛运动水平速度竖直方向自由落体速度，速度合成遵循矢量法则如图?
?
，

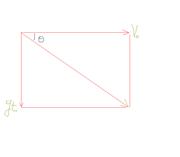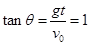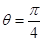
本题难度：一般

3、填空题  在光滑斜面的底端静置一个物体，从某时刻开始有一个沿斜面向上的恒力F作用在物体上，使物体沿斜面向上滑去，经一段时间撤去这个力，又经过相同的时间物体返回斜面的底部，且具有120J的动能．则恒力F对物体所做的功为______J，撤去恒力F时，物体具有的动能为______J．

参考答案：对全过程运用动能定理，重力不做功，只有恒力做功，则WF=12mv2-0=120J．
设撤去恒力F时的速度为v′，返回出发点的速度为v，根据平均速度的公式有：v′2t=-v′-v2t，解得v=2v′
则撤去F时的动能是回到出发点动能的14，所以撤去F时的动能EK=14×120J=30J．
故答案为：120，30．

本题解析：

本题难度：简单

4、简答题  如图所示：两块带电金属板a、b水平正对放置，在板间形成匀强电场，电场方向竖直向上．板间同时存在与电场正交的匀强磁场，假设电场、磁场只存在于两板间的空间区域．一束电子以一定的初速度v0从两板的左端中央，沿垂直于电场、磁场的方向射入场中，无偏转的通过场区．
已知：板长L=10.0cm，两板间距d=3.0cm，两板间电势差U=150V，v0=2.0×107m/s．电子所带电量与其质量之比e/m=1.76×1011C/kg，电子电荷量1.60×10-19C，不计电子所受的重力和电子之间的相互作用力．求：
（1）求磁感应强度B的大小
（2）若撤去磁场，求电子离开电场时偏离入射方向的距离y
（3）若撤去磁场，求电子穿过电场的整个过程中动能的增加量△EK（4）．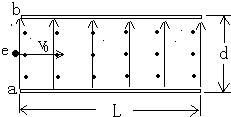

参考答案：
（1）由平衡条件得
? eUd=ev0B，得，B=Uv0d=2.5×10-4T
（2）若撤去磁场，电子做平抛运动．
水平方向：L=v0t
竖直方向：y=12at2，a=eUmd
联立得到，y=eUL22mdv20
代入解得，y=1.1×10-2m
（3）根据动能定理得
? 动能的增加量△EK=eEy=eUdy
代入解得，△EK=8.8×10-18J
答：
（1）磁感应强度B的大小为2.5×10-4T．
（2）若撤去磁场，求电子离开电场时偏离入射方向的距离y=1.1×10-2m．
（3）若撤去磁场，求电子穿过电场的整个过程中动能的增加量△EK=8.8×10-18J．

本题解析：

本题难度：一般

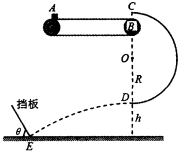
5、简答题  如图所示，质量为m=lkg的小物块由静止轻轻放在水平匀速运动的传送带上，从A点随传送带运动到水平部分的最右端B点，经半圆轨道C点沿圆弧切线进入竖直光滑的半圆轨道，恰能做圆周运动．C点在B点的正上方，D点为轨道的最低点．小物块离开D点后，做平抛运动，恰好垂直于倾斜挡板打在挡板跟水平面相交的E点．已知半圆轨道的半径R=0.9m，D点距水平面的高度h=0.75m，取g=10m/s2，试求：
（1）摩擦力对物块做的功；
（2）小物块经过D点时对轨道压力的大小；
（3）倾斜挡板与水平面间的夹角θ．

参考答案：（1）设小物块经过C点时的速度大小v1，因为经过C时恰好能完成圆周运动，由牛顿第二定律可得：
mg=mv21R，解得v1=3m/s
小物块由A到B过程中，设摩擦力对小物块做的功为W，由动能定理得：
W=12mv21，解得W=4.5J
故摩擦力对物块做的功为4.5J．
（2）设小物块经过D点时的速度为v2，对由C点到D点的过程，由动能定理的：
mg.2R=12mv22-12mv21
小物块经过D点时，设轨道对它的支持力大小为FN，由牛顿第二定律得：
FN-mg=mv22R
联立解得FN=60N，v2=3

本题解析：

本题难度：简单